DRL Multi-Agent Reinforcement Learning
Updated:
Chapter 9. Multi-Agent Reinforcement Learning
(멀티-에이전트 강화 학습)
(Orinial Book = ‘Deep Reinforcement Learning in Action’ by Alexander Zai and Brandon Brown)
이 장에서 다룰 내용 :
- 멀티 에이전트 설정에서 일반적인 Q-learning이 실패 할 수 있는 이유
- 멀티 에이전트와 함께 “차원의 저주”를 다루는 방법
- 다른 에이전트를 인식 할 수 있는 멀티 에이전트 Q-learning 모델을 구현하는 방법
- 평균 필드 근사(Mean Field Approximation)를 사용하여 다중 에이전트 Q-learning 을 확장하는 방법
- 멀티 에이전트 물리 시뮬레이션 및 게임에서 DQN을 사용하여 수십 개의 에이전트를 제어
9.1 하나에서 여러 에이전트로
지금까지 다룬 강화 학습 알고리즘 : Q-learning, Policy Gradient, Actor-Critic 알고리즘은 모두 환경에서 단일 에이전트를 제어하는 경우에 적용되었다. 그러나 서로 상호 작용할 수 있는 둘 이상의 에이전트를 제어하려는 상황에 대해서는 어떨까? 가장 간단한 예는 각 플레이어가 강화 학습 에이전트로 구현되는 2인용 게임이다. 교통 시뮬레이션과 같이 서로 상호 작용하는 수백 또는 수천의 개별 에이전트를 모델링하려는 다른 상황도 있다. 이 장에서는 먼저 Yang et al. 의 2018년 “Mean Field Multi-Agent Reinforcement Learning” 라는 논문에 설명된 MF-Q(Mean Field Q-learning)라는 알고리즘을 구현하여 지금까지 배운 내용을 멀티 에이전트 시나리오에 적용하는 방법을 배운다.
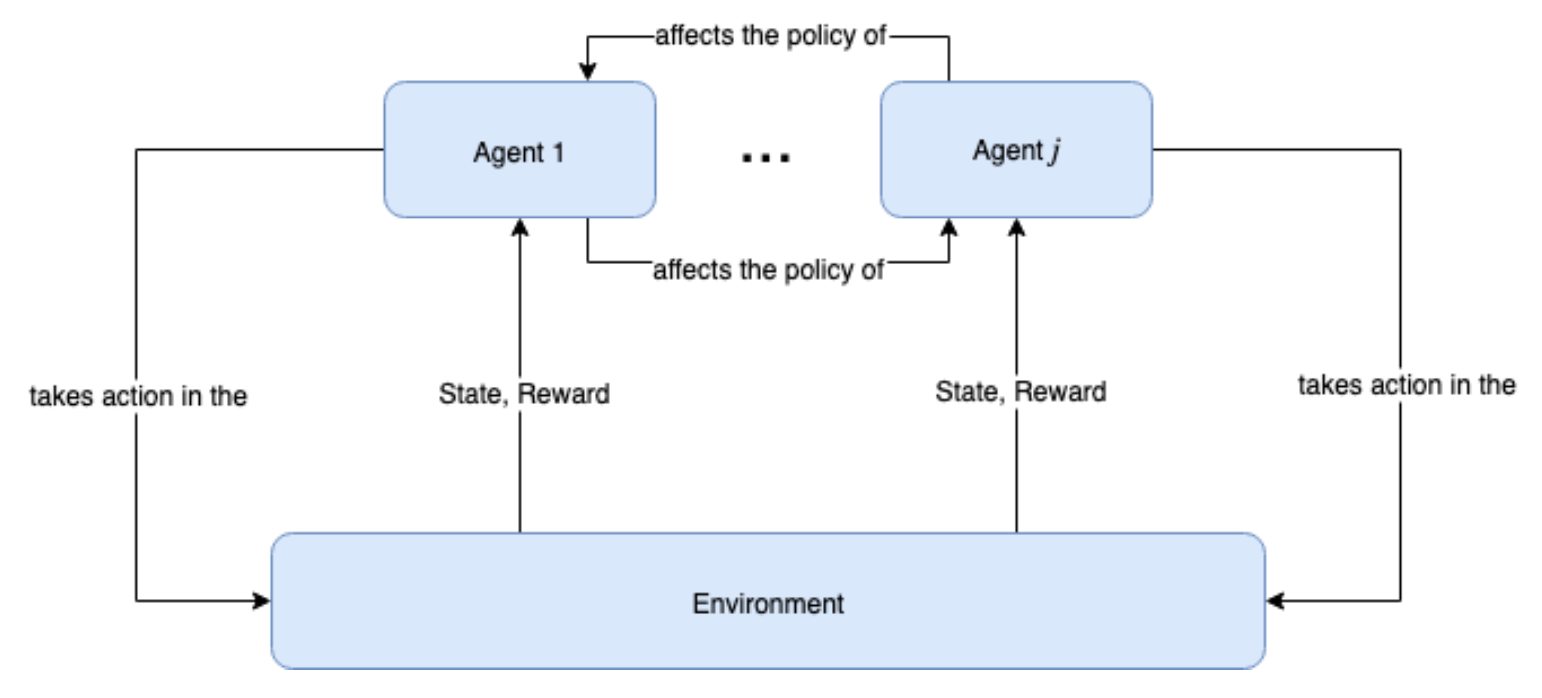
Figure 9.1: 멀티 에이전트 설정에서 각 에이전트의 Action은 환경의 진화뿐만 아니라 다른 에이전트의 Policy에도 영향을 미치므로 에이전트의 상호 작용이 매우 다이나믹하다. 환경은 각 에이전트 1, …, j 에 대해서 State 및 Reward을 생성한다. 각 에이전트는 이 State 와 Reward를 가지고 자체 Policy을 사용하여 Action를 취하는 데 사용한다. 그러나 각 에이전트의 Policy는 다른 모든 에이전트의 Policy에 영향을 미친다.
게임의 경우 환경에는 우리가 제어하지 못하는 다른 에이전트가 포함되어 있을 수 있다. 예를 들어, 8장에서 NPC(non-player characters)가 많은 Super Mario Bros. 게임을 보자. 이 NPC는 보이지 않는 다른 게임 로직에 의해 제어되지만 종종 메인 플레이어와 상호 작용할 수 있다. 예를 들어, DQN(Deep Q-network) 에이전트의 관점에서 볼 때 이러한 NPC는 시간이 지나면서 변화하는 환경 State의 패턴에 지나지 않다. DQN은 다른 플레이어의 행동을 직접 인식하지 못한다. 그러나 이러한 NPC는 학습하지 않기 때문에 문제가 되지 않는다. NPC는 고정된 Policy를 가지고 있다.
그러나 심층 강화 학습 알고리즘을 사용하여 일부 환경에서 다수의 상호 작용 에이전트의 동작을 직접 제어한다고 상상해 보자. 예를 들어, 여러 플레이어가 팀으로 그룹화된 게임이 있으며 팀에서 다른 팀에 대해 많은 플레이어를 재생할 수 있는 알고리즘을 개발할 수 있다. 또는 교통 패턴을 모델링하기 위해 수백 대의 시뮬레이션된 자동차의 동작을 제어 할 수 있다. 또는 경제학자가 경제 모델에서 수천 명의 에이전트의 행동을 모델링하려고 할 수도 있다. 이런 경우는 NPC와는 다른 상황이다. NPC와 달리 이러한 에이전트 각각은 모두 학습을 하고 한 에이전트의 학습은 다른 에이전트들에게 영향을 준다.
우리가 이미 알고있는 것을 멀티 에이전트 설정으로 확장하는 가장 간단한 방법은 각 에이전트에 대해 multiple DQN(또는 다른 유사한 알고리즘)을 인스턴스화 한 다음 각 에이전트는 환경을 그대로 보고 Action을 취하는 것이다. 우리가 통제하려는 에이전트가 모두 같은 Policy를 사용하는 경우(예를 들어, 각 플레이어가 Identical한 멀티 플레이어 게임에서) 합리적인 가정이라면 single DQN을 재사용하여 멀티 에이전트를 모델링 할 수도 있다(예 : 단일 매개 변수 집합).
이 접근법을 독립 Q-learning (Independent Q-learning, IL-Q)이라고 하며, 합리적으로 잘 작동하지만 에이전트 간의 상호 작용이 각각의 의사 결정에 영향을 미친다는 사실을 놓치고 있다. IL-Q 알고리즘을 사용하면 각 에이전트는 다른 에이전트가 수행하는 Action과 해당 작업이 자신에게 어떤 영향을 미치는지 완전히 알 수 없다. 각 에이전트는 다른 에이전트의 현재 State를 포함하는 환경의 State 표현만 가져 오지만 본질적으로 환경에서 다른 에이전트의 활동을 노이즈로 처리한다(다른 에이전트의 Action은 대부분 부분적으로만 예측 가능하므로).
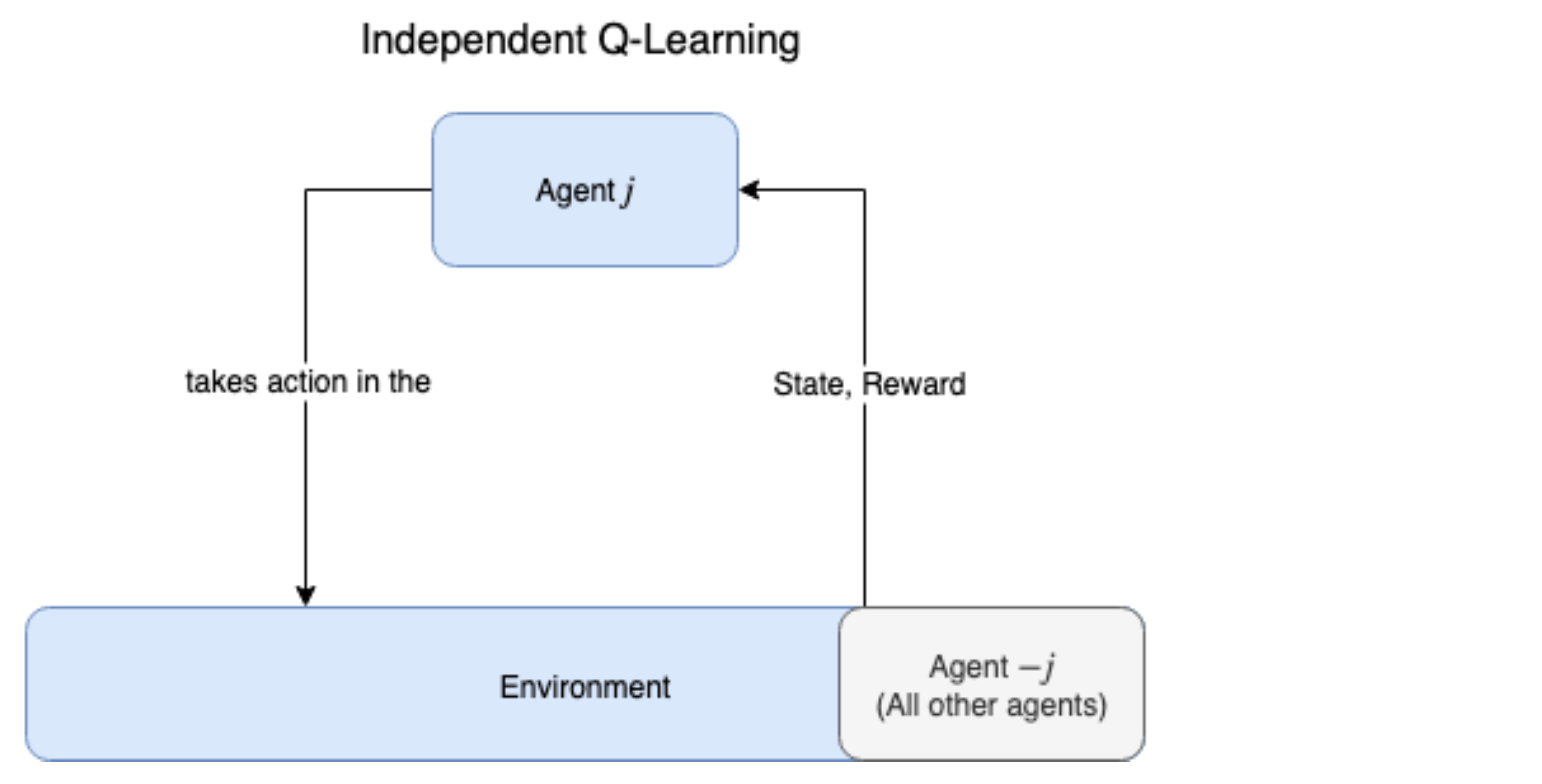
Figure 9.2 독립 Q-learning(Independent Q-learning)에서 각 에이전트는 다른 에이전트의 Action을 직접 인식하지 않고 다른 에이전트들은 단지 환경의 일부인 것처럼 가장한다. 이는 다른 에이전트가 환경을 고정적이지 않게 만들기 때문에 Q-learning이 단일 에이전트 설정에서 받았던 장점을 그대로 보장받지 못한다.
지금까지 수행한 일반적인 Q-learning은 환경에 단일 에이전트만 있었다. Q-function이 최적의 값으로 수렴되므로 Optimal Policy에 수렴된다(수학적으로 오랜 시간에 걸쳐 수렴됨이 보장됨). 이는 단일 에이전트 설정에서 환경이 고정(Stationary)되어 있기 때문에 주어진 State에서 특정 Action에 대한 Reward 분포가 항상 동일하다는 것을 의미한다. 이 Stationarity Feature은 멀티 에이전트 설정에서 통하지 않는다. 개별 에이전트가 받는 Reward는 자체 Action뿐만 아니라 다른 에이전트의 Action에 따라 달라지기 때문이다. 이는 모든 에이전트가 강화 학습 에이전트이며 경험을 통해 학습하기 때문에 환경 변화에 따라 Policy가 지속적으로 변경되기 때문이다. 이 고정되지 않은 환경에서 IL-Q를 사용하면 수렴 보장을 잃게되므로 독립 Q-learning (Independent Q-learning)의 성능이 크게 저하 될 수 있다.
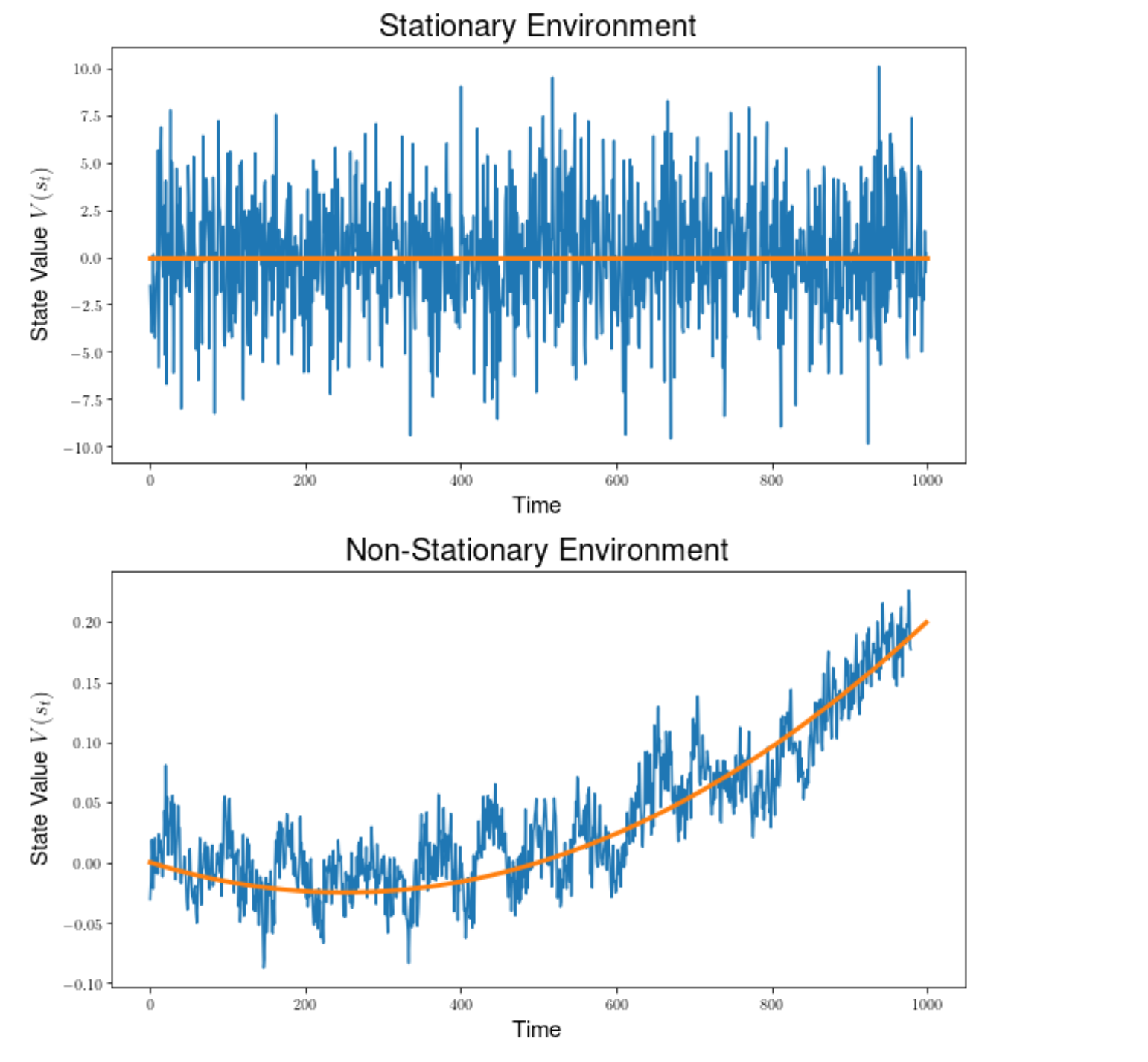
그림 9.3 정적(Stationary) 환경에서 주어진 State에 대한 기대값(예 : 평균)은 일정하게 유지된다(Stationary). 특정 State 전이는 확률적 구성 요소를 가질 수 있으므로 노이지해 보이는 시계열이지만 시계열의 평균은 일정하다. 비정적(Non-stationary) 환경에서, 주어진 State 전이에 대한 기대값은 시간이 지남에 따라 변경 될 것이며, 이는 이 시계열에서 시간에 따라 변화하는 평균 또는 기준선으로 표시된다. Q-function은 State-Action에 대한 기대값을 학습하려고 시도하고 State-Action value가 고정된 경우에만 수렴 할 수 있지만 다중 에이전트 설정에서는 예상 State-Action value가 다른 에이전트의 진화하는 Policy 때문에 계속 바뀐다 .
일반적인 Q-function은 함수 Q(s, a) : SxA → R 이고 이것은 State-Action 쌍에서 Reward(실수)로 가는 함수이다. 우리는 다른 에이전트의 Action에 대한 지식을 포함하는 약간 더 복잡한 Q-function를 만들어 IL-Q 관련 문제를 해결할 수 있다. Qj (s, aj, a- j):S × A j × A− j → R은 State, 에이전트 j의 Action 및 기타 모든 에이전트 Action (-j, “not j”로 표시)을 가진 튜플에 대해 Expected Reward(실수)로 가져 오는 j로 색인화된 에이전트에 대한 Q-function이다. 이 Q-function은 결국 Optimal Value function과 Optimal Policy function이 학습되도록 수렴하는 것을 보증한다. 수정된 Q-function은 훨씬 더 잘 수행 된다.
불행하게도, Joint Action space a-j가 매우 크고 에이전트의 수에 따라 지수적으로 증가하기 때문에,이 새로운 Q-function은 일반적으로 다루기 힘들다(에이전트의 수가 많은 경우). Action을 어떻게 인코딩하는지 기억하는가? Action 수와 같은 길이의 벡터를 사용한다. 단일 Action을 인코딩하려면 Action에 해당하는 위치(1로 설정)를 제외하고 모든 요소가 0 인 one-hot 벡터로 만든다. 예를 들어 Gridworld 환경에서 에이전트는 4 가지 동작 ( 위, 아래, 왼쪽, 오른쪽) Action을 길이가 4인 벡터로 인코딩한다. 여기서 [1,0,0,0]은 “up”으로 인코딩되고 [0,1,0,0]은 “down” 식으로 기타 등등.
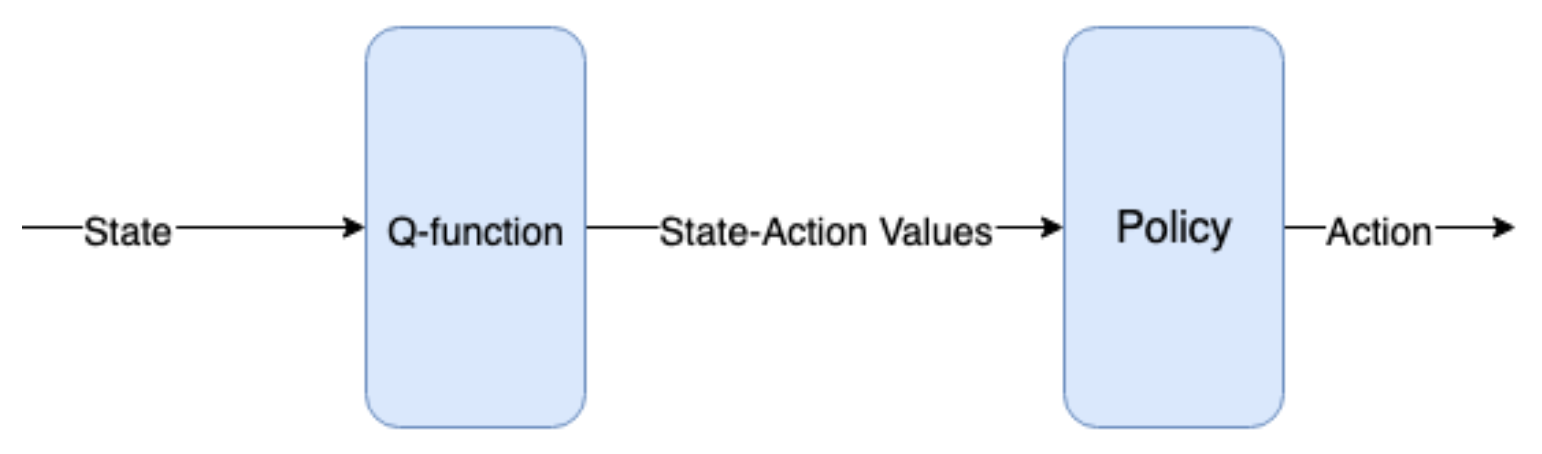
Figure 9.4 Q-function은 State를 취하고 State-Action value(Q-value)을 생성한 다음 Policy 함수가 Action을 생성하는 데 사용한다. 대안적으로 State를 취하고 Action에 대한 확률 분포를 반환하는 Policy 함수를 직접 학습할 수도 있다.
Policy π(s) : S → A는 State를 취하고 Action를 리턴하는 함수이다. Deterministic Policy인 경우 이러한 one-hot 벡터 중 하나를 반환하거나 Stochastic Policy인 경우 Action에 대한 확률 분포를 반환한다(예 : [0.25,0.25,0.2,0.3]). Joint Action space가 지수적으로 증가하는 것은 예를 들어 Gridworld에서 각각 4개의 Action을 가진 두 에이전트의 Joint Action과 같이 Joint Action을 명확하게 인코딩하려면 길인가 4인 벡터 대신 4^2 = 16 길이의 one-hot 벡터를 사용해야 한다는 사실에 기인한다. 이는 두 에이전트 사이에 각각 4개의 Action(Figure 9.5 참조)를 갖는 16가지의 가능한 조합이 있기 때문이다. [에이전트 1 : Action 1, 에이전트 2 : Action 4], [에이전트 1 : Action 3, 에이전트 2 : Action 3] 등.
| 3개의 에이전트의 Joint Action을 모델링하려면 4^3 = 64 길이의 벡터를 사용해야 한다. 따라서 Gridworld의 경우 일반적으로 4^N 길이 벡터를 사용해야 한다. 여기서 N은 에이전트 수이다. 어떤 환경에서든 Joint Action 벡터의 크기는 | A | ^N 이다. 여기서 | A | 는 Action space의 크기(즉, 개별 Action의 수)를 나타낸다. 그것은 에이전트의 수에서 지수적으로 커지는 벡터이며, 이것은 에이전트가 많아지면 매우 비현실적이고 다루기 힘들어 질것이다. 지수적으로 커진다는 것은 알고리즘이 확장 될 수 없다는 것을 의미하기 때문에 항상 나쁜 것이다. |
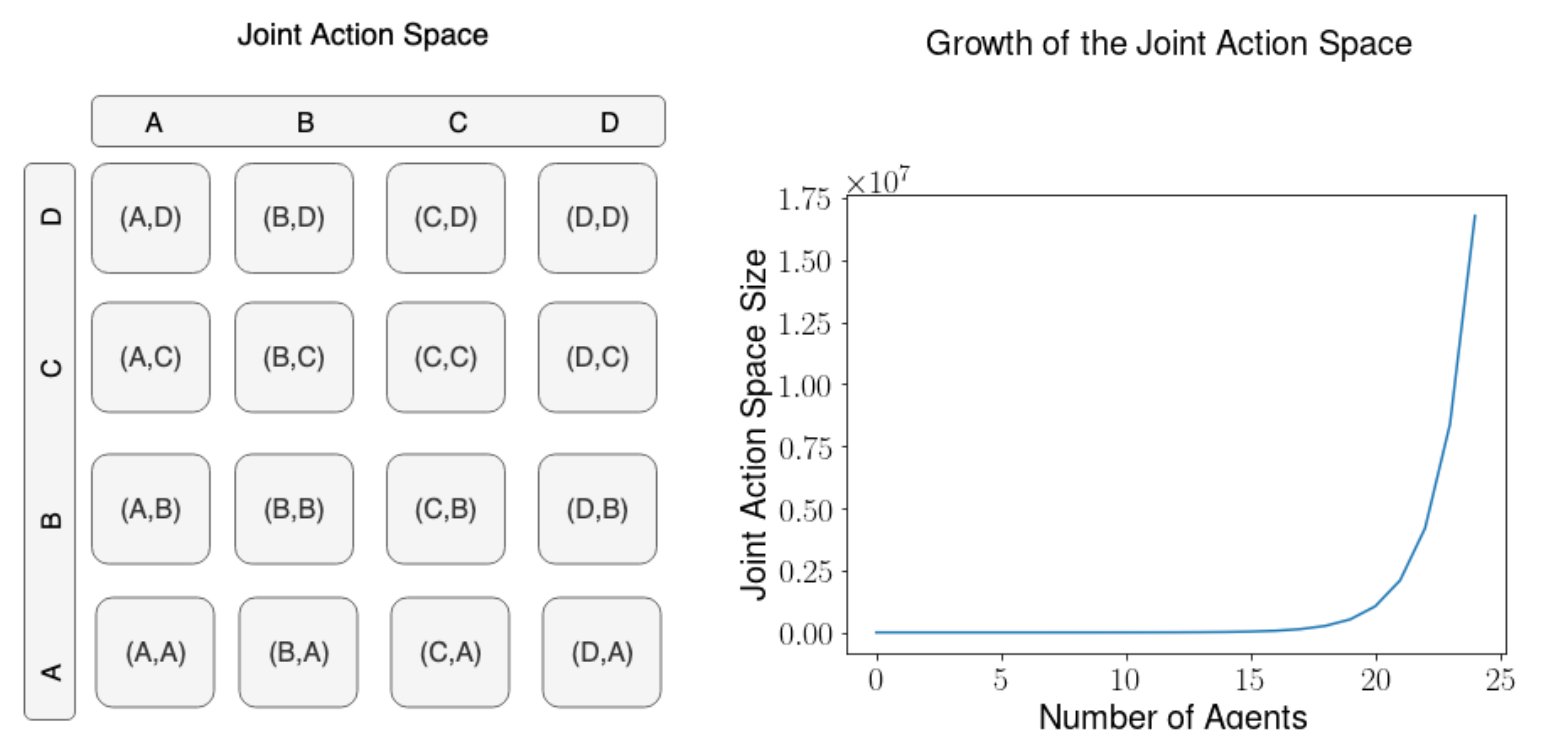
Figure 9.5 각 에이전트의 크기가 4인 Action space(즉, 4 요소 one-hot 벡터로 표시)이 있는 경우, 두 에이전트의 Joint Action space는 4^2 = 16 또는 4^N이며 여기서 N은 에이전트 수이다. 이는 Joint Action space의 증가가 에이전트 수에서 지수적임을 의미한다. 오른쪽 그림은 크기가 2인 개별 Action space을 가진 에이전트에 대한 Joint Action space 크기를 보여준다. 25개의 Agent 만 있어도 Joint Action space는 33,554,432 개의 요소 one-hot 벡터가 되어 계산하기에 비실용적이다.
이 지수적으로 큰 Joint Action space은 MARL이 초래하는 새로운 주요 문제이며 이 장에서 해결해야하는 문제이다.
9.2 Neighborhood Q-learning
비현실적으로 매우 큰 Joint Action space 문제를 해결할 수 있는 Action 및 Joint Action을 표현하는 보다 효율적이고 간결한 방법이 있는지 궁금 할 수 있지만 불행히도 더 컴팩트한 인코딩을 사용하여 Action을 표현할 수 있는 명확한 방법은 없다. 에이전트들이 단일 숫자를 사용하여 수행한 Action을 명확하게 전달할 수 있는 방법에 대해 생각해 보면 지수적으로 큰 Joint Action space를 사용하는 방법보다 더 좋은 방법이 없음을 알게 될것이다.
이 시점에서 MARL이 그리 실용적으로 보이지 않을 것이다. 그러나 이상적인 Joint Action Q-function에 대한 근사를 만들어 MARL을 실용적으로 만들 수 있다. 옵션 하나는 대부분의 환경에서 서로 가까이 있는 에이전트만 서로에게 큰 영향을 줄 것임을 인식하는 것이다. 따라서 환경에 있는 모든 에이전트의 Joint Action을 반드시 모델링 할 필요는 없으며, 동일한 이웃(neighborhood)에 있는 에이전트의 Joint Action 만 모델링하여 이를 추정 할 수 있다. 어떤 의미에서, 우리는 전체 Joint Action space을 겹치는 부분 공간(subspace)으로 나누고 이 작은 부분 공간에 대해서만 Q-value을 계산하는 것이 된다. 이 방법을 이웃 Q-learning(Neighborhood Q-learning) 또는 부분 공간 Q-learning(Subspace Q-learning)이라고 부를 수 있습니다.
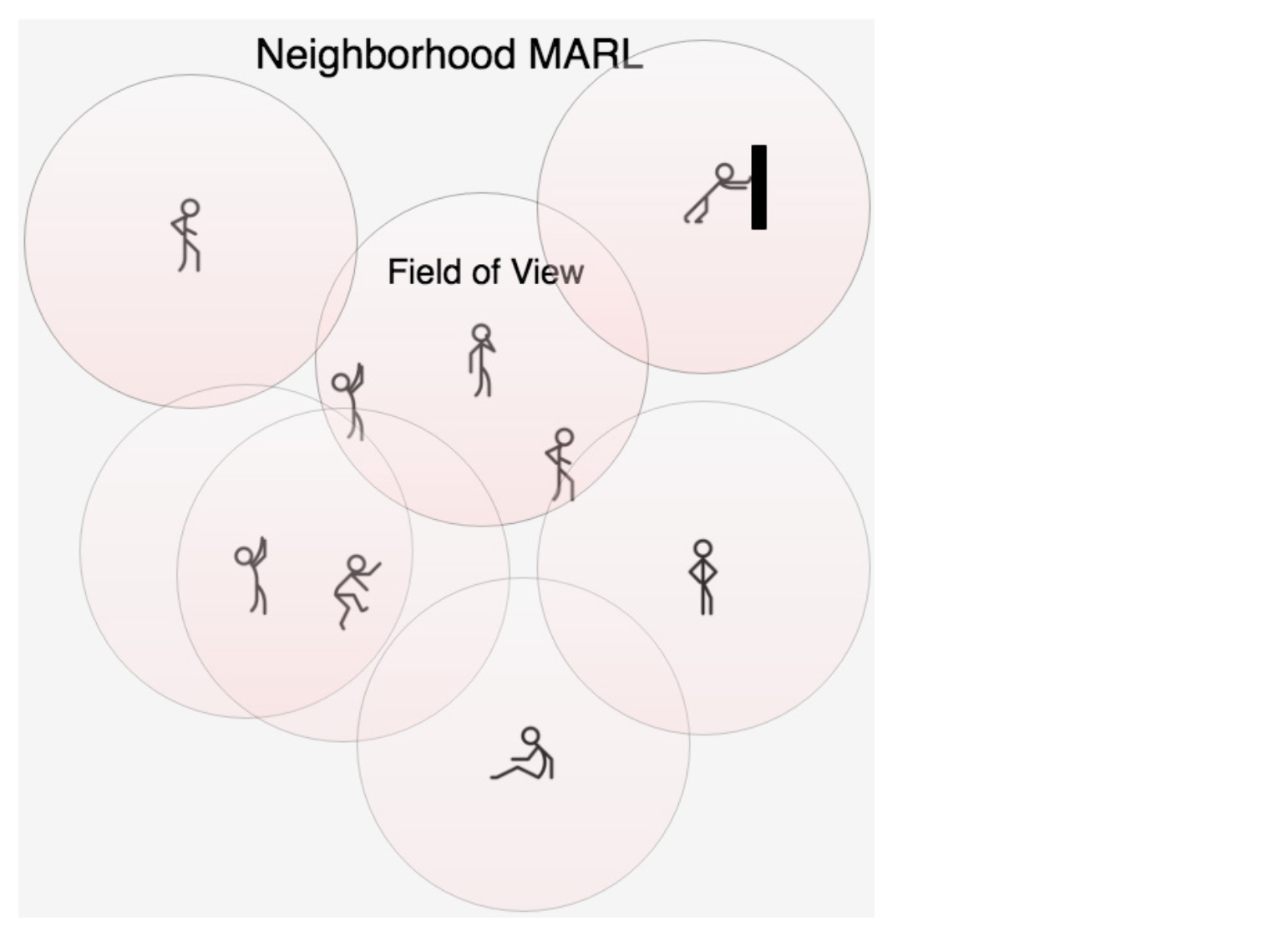
Figure 9.6 Neighborhood MARL 에서, 각 에이전트는 FOV(Field of View) 또는 이웃(neighborhood)을 가지며 해당 이웃 내의 다른 에이전트의 Action만 볼 수 있다. 그러나 각 에이전트는 여전히 환경에 대한 전체 State 정보를 얻을 수 있다.
이웃의 크기를 제한함으로써, 우리는 이웃 space을 설정이 고정된 크기가 되도록하여 Joint Action space의 지수적 성장을 막는다. 각 에이전트에 4개의 액션과 총 100개의 에이전트가 있는 멀티 에이전트 Gridworld가 있는 경우 전체 Joint Action space은 4^100 이며, 이 크기는 다루기 힘든 크기이므로 이렇게 큰 벡터는 컴퓨터로 계산하거나 저장하지 못할 수도 있다. 그러나 Joint Action space의 부분 공간(subspace)을 사용하고 각 부분 공간(neighborhood)의 크기를 3(고정된 각 부분 공간의 크기는 4^3 = 64)으로 고정되도록 설정하면 이 값이 단일 에이전트일 때보다는 큰 벡터이긴 하지만 확실히 우리가 계산할 수 있는 범위 안에 있다. 이 경우, 에이전트 1에 대한 Q-value을 계산하는 경우 에이전트 1과 가장 가까운 3개의 에이전트를 찾은 다음 이 3개의 에이전트에 대해 길이가 64인 Joint Action one-hot 벡터를 만들어 Q-function에 보낸다. 그래서 각 에이전트의 총합이 100인 경우 이러한 부분 공간(subspace) Joint Action 벡터를 만들고 이를 사용하여 각 에이전트의 Q-value을 계산 한 다음 해당 Q-value을 이용하여 평소와 같이 Action를 취한다.
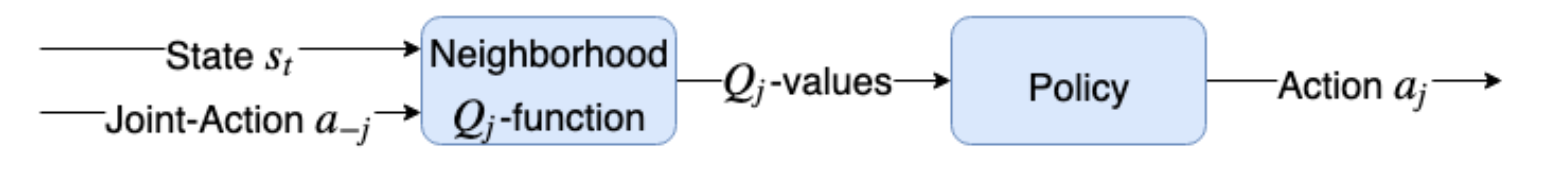
Figure 9.7 에이전트 j 의 Neighborhood Q-function은 aj로 표시되는 해당 neighborhood (또는 Field of View) 내의 다른 에이전트에 대한 현재 State 및 Joint Action 벡터를 받아들 Action를 선택하는 Policy 함수에 전달되는 Q-value을 생성한다.
이것이 어떻게 작동하는 지에 대한 Pseudocode를 작성해 보자 .
Listing 9.1 Pseudocode for Neighborhood Q-learning, part 1
# Initialize actions for all agents
for j in agents: #A
state = environment.get_state() #B
neighbors = get_neighbors(j, num=3) #C
joint_action = get_joint_action(neighbors) #D
q_values = Q(state, joint_action) #E
j.action = policy(q_values) #F
environment.take_action(j.action)
reward = environment.get_reward()
#A List에 저장된 환경의 모든 에이전트를 반복한다.
#B 현재 환경으로 부터 상태를 가져온다.
#C 에이전트 j에 가장 가까운 에이전트 3개를 찾는다.
#D 에이전트 j의 이웃의 Joint Action을 반환한다.
#E State와 이웃의 Joint Action을 고려하여 에이전트 j의 각 Action에 대한 Q-value을 가져온다.
#F Q-value을 사용하여 개별 Action을 반환한다.
현재 에이전트 j를 가져와 가장 가까운 3개의 이웃을 찾는 함수가 필요하다. 그런 다음 가장 가까운 3개의 이웃을 사용하여 Joint Action을 만드는 함수가 필요하다. 이 시점에서 또 다른 문제가 있다. 다른 에이전트의 Action을 모르고 어떻게 Joint Action을 만들까? 에이전트 j에 대한 Q-value를 계산하여 Action을 취하려면 에이전트 -j가 수행하는 Action을 알아야 한다(에이전트 j가 아닌 에이전트를 표시하기 위해 -j를 사용하지만 이 경우에는 가장 가까운 이웃 만을 말함). 그러나 에이전트 -j의 Action을 파악하려면 모든 Q-value를 계산해야 한다. 이것은 시간이 매우 오래 걸리는 작업이다.
이 문제를 피하기 위해 에이전트를 시작할 때 에이전트에 대한 모든 Action을 무작위로 초기화한 다음 무작위로 초기화된 Action를 사용하여 Joint Action을 계산할 수 있다. 그러나 Joint Action을 사용하는 것이 무작위이기 때문에 큰 도움이 되지 않을 것이다. 따라서 이 과정을 몇 번 다시 실행한다( for m in range(M) 에서 M을 5와 같은 작은 숫자로 설정). 처음 실행하면 Joint Action이 임의적이지만 모든 에이전트는 Q-function을 기반으로 작업을 수행하므로 두번째 실행에는 약간 덜 무작위적이며 몇 번 더 계속하면, 초기 무작위성이 충분히 희석될 것이고 실제 환경에서 이 반복이 끝날 때쯤이면 실제로 적당한 Action을 취할 수 있게 된다.
Listing 9.2 Pseudocode for Neighborhood Q-learning, part 2
# Initialize actions for all agents
for m in range(M): #A
for j in agents:
state = environment.get_state()
neighbors = get_neighbors(j, num=3)
joint_actions = get_joint_action(neighbors)
q_values = Q(state, joint_actions)
j.action = policy(q_values)
for j in agents: #B
environment.take_action(j.action)
reward = environment.get_reward()
#A 초기 임의성을 희석하기 위해 Joint Action 및 Q-value를 몇 번 계산하는 과정을 반복한다.
#B 이전 루프에서 계산된 최종 Action을 실제로 수행하려면 에이전트를 다시 반복해야 한다.
개별 Action 집합에서 Joint Action을 만드는 방법은 선형 대수의 외적(Outer Product) 연산을 사용하는 것이다. 이것을 표현하는 가장 간단한 방법은 일반 벡터를 행렬로 “Promote”하는 것이다. 예를 들어, 길이가 4인 벡터를 4x1 행렬로 승격(promote)시킬 수 있다. PyTorch와 Numpy에서는 텐서에서 reshape 방법을 사용하여 이 작업을 수행 할 수 있다(예 : torch.Tensor([1,0,0,0]).reshape(1,4) ). 두 행렬을 곱할 때 얻을 수 있는 결과는 크기와 곱하는 순서에 따라 다르다. 행렬 A : 1 × 4 을 가져 와서 다른 행렬 B : 4 × 1 와 곱하면 1 x 1 결과가 나온다. 이는 스칼라(단일 숫자)이다. 두개의 큰 차원이 두 개의 단일 차원 사이에 끼워져 있기 때문에 이것은 두 개의 벡터(행렬로 승격됨)의 내적이다. 외적은 이것과 반대이다. 두 개의 큰 차원이 외부에 있고 두 개의 단일 차원이 내부에 있기 때문에 [4 × 1] × [1 × 4] = 4 × 4 행렬이 된다.
Gridworld에 개별 Action [0,0,0,1] ( “오른쪽”) 및 [0,0,1,0] ( “왼쪽”)을 가진 두 개의 에이전트가있는 경우 이 벡터의 외적. 다음은 numpy에서 수행하는 방법이다.
>>> np.array([[0,0,0,1]]).T @ np.array([[0,1,0,0]])
array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 1, 0, 0]])
결과는 4x4 행렬이며 위에서 계산한 총 16 개의 요소가 있습니다. 두 행렬 사이의 외적 결과의 차원은 dim(A) * dim(B)입니다. 여기서 A와 B는 벡터이고dim은 벡터의 크기(차원)를 나타낸다. 외적은 Joint Action space가 지수적으로 증가하는 이유를 설명한다. 일반적으로 신경망을 적용한 Q-learning에서는 벡터인 입력이 필요하므로 외적의 결과인 행렬을 벡터로 평탄화(Flatten) 한다.
>>> z = np.array([[0,0,0,1]]).T @ np.array([[0,1,0,0]])
>>> z.flatten()
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0])
여기까지만 보면, 이웃 Q-learning 접근법이 일반적인 Q-learning보다 그렇게 복잡하지 않다는 것을 알 수 있다. 각 에이전트의 가장 가까운 이웃의 Joint Action 벡터인 추가 입력을 제공하기만 하면 된다. 실제 문제를 해결하면서 세부 사항을 알아 보자.
9.3 1차원 Ising 모델(1-Dimensional Ising Model)
이 섹션에서는 MARL을 적용하여 1920년대 초 물리학자 Wilhelm Lenz와 그의 학생인 Ernst Ising이 처음 설명했던 먼저 간단한 실제 물리 문제를 풀어 본다. 물리학자들은 수학적 모델에 의해 철과 같은 자성 물질의 움직임을 이해하려고 했다. 손에 쥐고 있을 수 있는 철 조각이 있다고 하자. 철 조각은 금속 결합(metallic bonding)으로 함께 그룹화된 철 원자의 모음이다. 원자는 양성자와 중성자와 전자라는 외부 “껍데기(shell)”로 구성된다. 전자는 다른 소립자처럼 스핀(Spin)이라는 성질을 가지고 있는데, 이 성질은 전자가 어떤 시간에 스핀 “위” 또는 스핀 “아래” 만을 가질 수 있도록 양자화(Quantized) 된다.
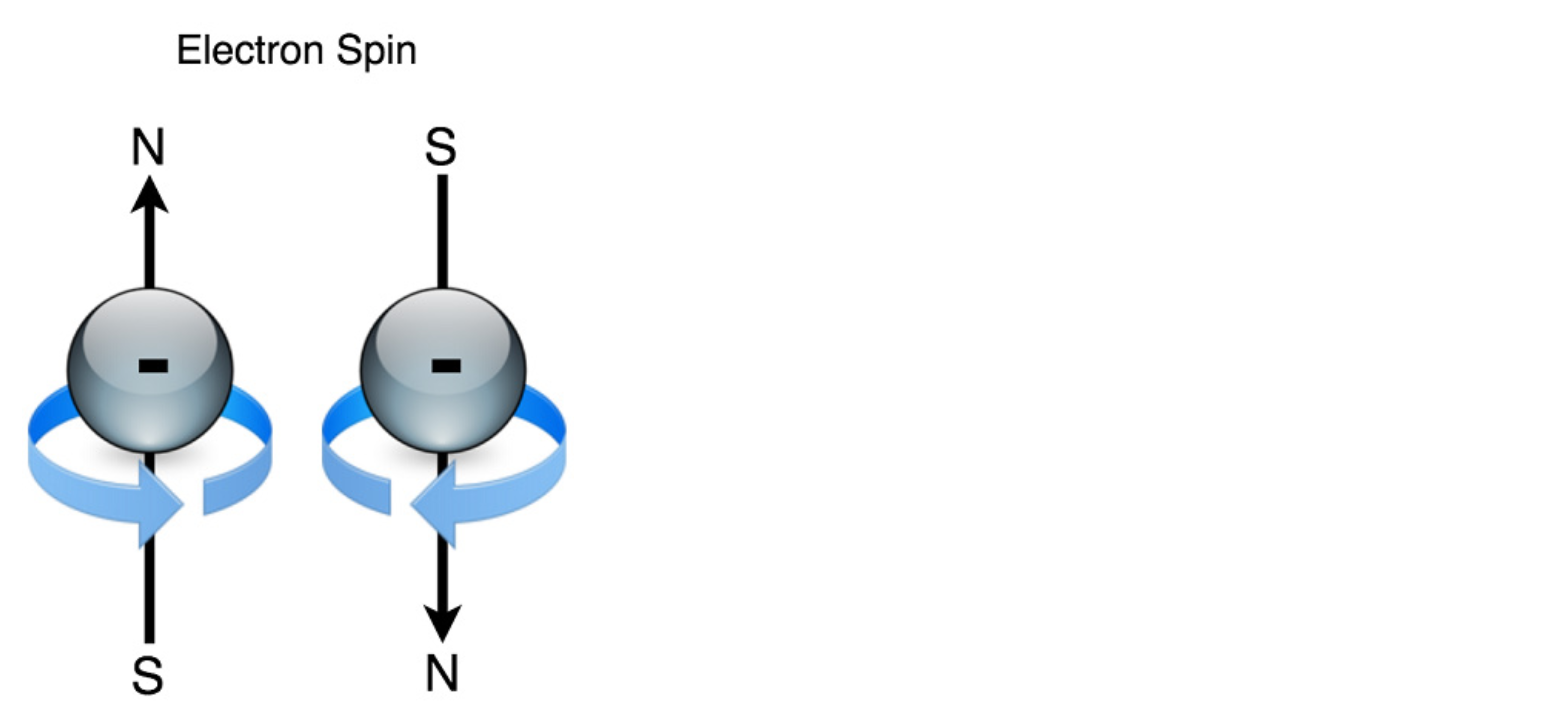
Figure 9.8 전자는 원자의 핵을 둘러싸고 있는 음으로 하전된 기본 입자이다. 스핀(Spin)이라는 속성이 있으며 “스핀 업(Spin Up)”또는 “스핀 다운(Spin Down)”이 될 수 있다. 이들은 하전된 입자이기 때문에 자기장을 생성하며, 회전하는 방향에 따라 자기장의 극 방향 (북 또는 남)이 결정된다.
스핀 특성은 전자가 시계 방향 또는 시계 반대 방향으로 회전하는 것으로 생각할 수 있다. 스핀의 특성은 문자 그대로 맞는 것은 아니지만 스핀 특성을 설명하려는 목적으로는 충분하다. 충전된 물체가 회전하면 자기장이 생성되므로 고무 풍선을 가져 와서 카펫에 문지르면 정전기가 발생하여 주위로 회전하면서 풍선 자석이 생긴다(자력이 약한 자석이긴 하지만). 전자는 마찬가지로 스핀과 전하(electric charge)로 인해 자기장(magnetic field)을 생성하므로 전자는 실제로 매우 작은 자석이며 모든 철 원자에 전자가 있기 때문에 모든 전자가 같은 방향 정렬되면 전체 철 조각이 큰 자석이 될 수 있다(즉, 모든 전자가 스핀 업되거나 또는 모든 전자가 스핀 다운되거나).
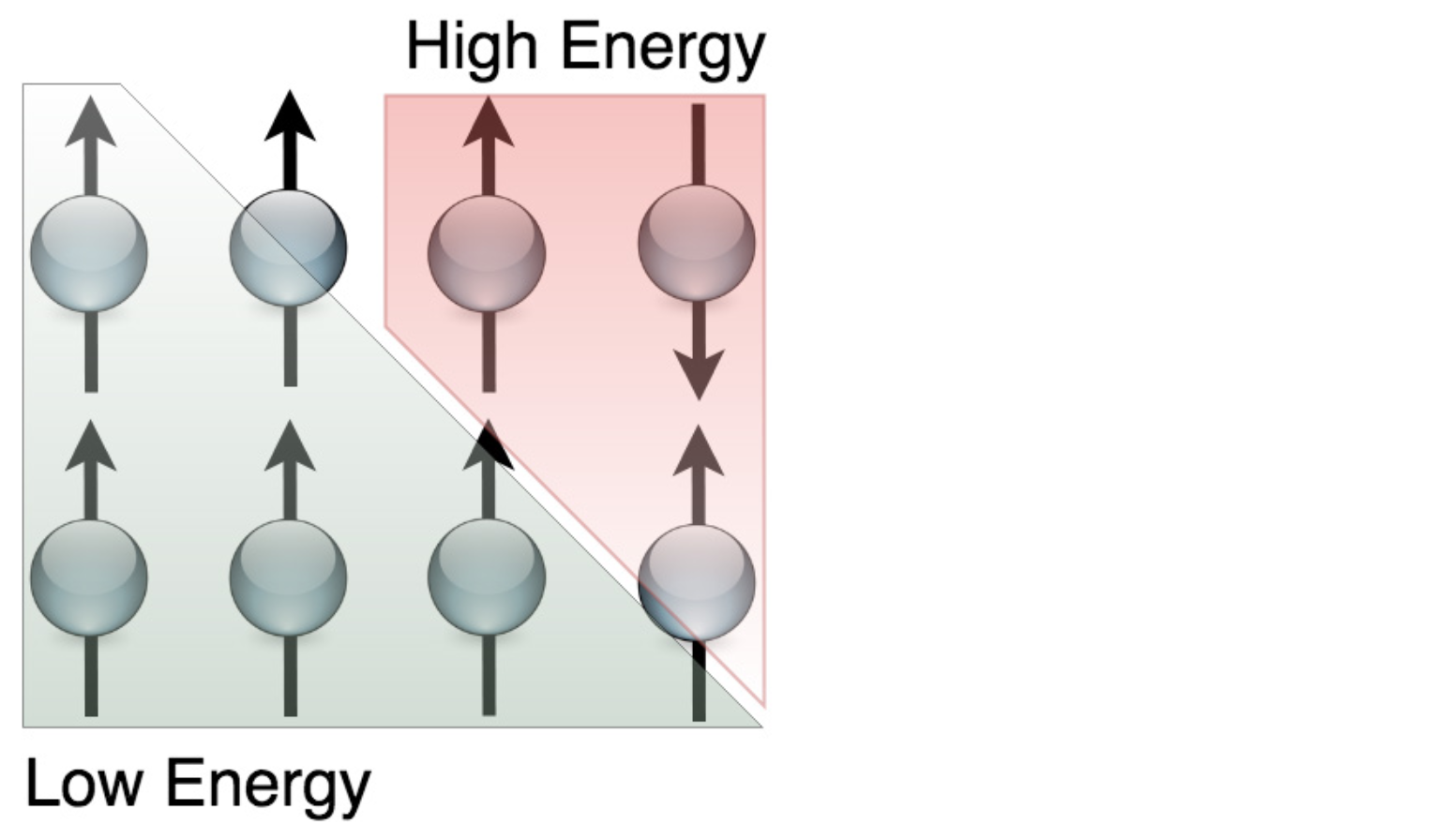
Figure 9.9 전자들이 채워질 때, 스핀이 정렬되지 않을 때보다 에너지 구성이 낮고 모든 물리적 시스템이 더 낮은 에너지를 향하는 경향이 있기 때문에 스핀이 같은 방향으로 정렬되는 것을 선호한다.
물리학자들은 전자가 어떻게 자기 자신을 맞추기 위해 “결정”하는지, 그리고 철의 온도가 이 과정에 어떤 영향을 미치는지 연구하려고 했다. 자석을 가열하면 어떤 시점에서 정렬된 전자가 무작위로 스핀을 교대로 시작하여 재료의 순 자기장이 손실됩니다. 물리학자들은 개별 전자가 자기장을 생성하고 작은 자기장이 근처의 전자에 영향을 줄 것이라는 것을 알고 있었다. 두 개의 막대 자석을 사용해 본 적이 있다면 자연스럽게 한 방향으로 정렬되거나 반대 방향으로 튕겨 나옵니다. 전자도 같은 일을합니다. 전자도 같은 스핀이 되도록 정렬하려고 시도하는 것이 합리적이다.
복잡성이 한 가지 더 있다. 주어진 도메인의 전자가 모두 정렬 (스핀 업 또는 다운)되지만 다른 근처의 도메인이 반대 방향에 있는 작은 도메인으로 전자가 구성되기 때문에 임의의 철 조각은 일반적으로 자화되지 않는다. 개별 전자는 근처의 전자에 자신을 맞추는 경향이 있지만, 더 큰 규모로 이러한 도메인은 (평균적으로) 정렬되지 않도록 구성된다. 이는 도메인이 커질수록 (즉, 동일한 정렬을 가진 전자의 수가 증가함에 따라) 자기장이 커지고 이 벌크 자기장이 클수록 실제로 재료에 약간의 내부 변형이 발생하기 때문이다. 따라서 슈퍼 로컬 레벨에서 전자는 정렬되어 에너지를 최소화하지만 너무 많은 정렬이 이루어지고 자기장이 너무 강해지면 시스템의 전체 에너지가 증가하여 전자가 상대적으로 도메인(Domain)이라고 하는 작은 클러스터에만 정렬된다.

Figure 9.10 각 픽셀이 전자를 나타내는 고해상도 Ising 모델의 이미지입니다. 밝은 픽셀은 스핀 업되고 검은 픽셀은 스핀 다운된 것이다. 전자가 도메인 내 모든 전자가 정렬되어있는 도메인으로 구성되는 것을 볼 수 있다. 이 조직은 시스템의 에너지를 줄인다.
아마도 벌크 형태의 물질로 이루어진 전자 1조(trillion)개 사이의 상호 작용은 전자를 도메인으로 복잡하게 구성되도록 만들었겠지만, 그 많은 상호 작용을 모델링하는 것은 매우 어렵다. 물리학자들은 주어진 전자가 가장 가까운 이웃에 의해서만 영향을 받는다는 가정으로 이 현상을 설명했다. 이는 우리가 이웃 Q-learing에서 했던 것과 정확히 같은 가정이다.
놀랍게도, 우리는 많은 전자의 행동을 모델링하고 멀티 에이전트 강화 학습으로 대규모 출현 조직을 관찰 할 수 있다. 주목할 것은 전자의 에너지를 “보상(Reward)”으로 해석하는 것이다. 전자가 이웃과 정렬(align)하기 위해 스핀을 변경하면, Positive Reward를 주고, 반대로 정렬하기(anti-align)위해 스핀을 변경하면 Negative Reward를 준다. 모든 전자가 Reward를 극대화하려고 할 때, 이는 에너지를 최소화하려는 것과 동일하며 물리학자가 에너지 기반 모델을 사용할 때와 동일한 결과를 얻는다. 앞으로 살펴 보겠지만 Exploration/Exploitation 의양을 변경하여 시스템 온도를 모델링 할 수도 있다. Exploration에는 무작위로 Action을 선택하는 것이 포함되며, 고온(High temperature)은 무작위 변화도 포함된다. ‘Exploration’ 과 ‘High temperature’ 는 이런 점에서 매우 유사한 개념이다.
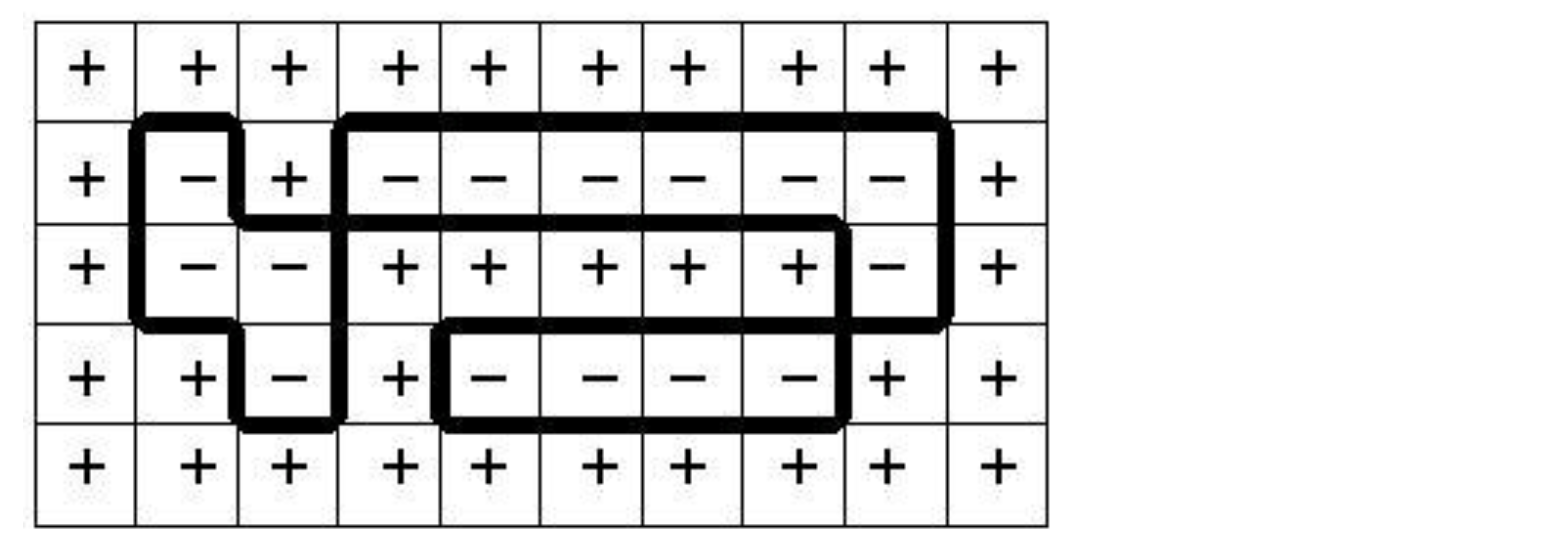
Figure 9.11 +는 스핀 업을, –는 스핀 다운을 전자 스핀의 2D Ising 모델을 나타낸다. 스핀 다운(검은 색으로 강조 표시된)된 전자로 이루어진 도메인이 있으며, 이 도메인은 스핀 업 전자 껍질로 둘러싸여 있다.
전자 스핀의 행동을 모델링하는 것은 중요하지 않은 것처럼 보일 수 있지만 전자에 사용되는 것과 동일한 기본 모델링 기술을 사용하여 유전학, 금융, 경제학, 식물학 및 사회학의 문제를 해결할 수 있다. MARL을 테스트하는 가장 간단한 방법 중 하나이기도 하다. 이것이 물리학 이야기를 꺼낸 주요 동기이다.
Ising 모델을 생성하기 위해 해야 할 유일한 것은 0은 스핀 다운을 나타내고 1은 스핀 업을 나타내는 이진수 그리드를 만드는 것이다. 이 그리드는 어떤 차원이 될 수도 있다. 1차원 그리드(벡터), 2차원 그리드(행렬) 또는 고차원 텐서가 있을 수 있다. 1D Ising Model은 Experience Replay이나 분산 알고리즘(Distributed Algorithm)과 같은 멋진 메커니즘을 사용할 필요가 없이 간단하다. 간단해서 PyTorch의 builtin Optimizer도 사용하지 않을 것이고, 몇 줄의 코드로 그라디언트 디센트를 수동으로 작성하겠다.
Listing 9.3 1D Ising Model
import numpy as np
import torch
from matplotlib import pyplot as plt
def init_grid(size=(10,)):
grid = torch.randn(*size)
grid[grid > 0] = 1
grid[grid <= 0] = 0
grid = grid.byte() #A
return grid
def get_reward(s,a): #B
r = -1
for i in s:
if i == a:
r += 0.9
r *= 2.
return r
#A 부동 소수점 숫자를 바이트 객체로 변환하여 이진수로 만든다.
#B `s`에서 이웃을 가져와 에이전트`a`와 비교하여 Reward를 바꾼다.
두 개의 함수를 만들었다. 첫 번째는 표준 정규 분포에서 가져온 수로 된 그리드를 만들어 무작위로 초기화된 1차원 그리드(벡터)를 만든 다음 모든 음수를 0으로 설정하고 모든 양수를 1로 설정한다. 그리드에 대략 같은 수의 1과 0의 요소를 넣는다. matplotlib을 사용하여 그리드를 시각화 할 수 있다.
>>> grid = init_grid(size=size)
>>> grid
tensor([1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0],
dtype=torch.uint8)
>>> plt.imshow(np.expand_dims(grid,0))

Figure 9.12 1D Ising Model, 단일 행으로 배열된 전자 스핀을 나타내고 있다.
1은 밝은색이며 0은 어두운색으로 나타냈다. plt.imshow는 행렬 또는 3차원 텐서에서만 작동하므로 np.expand_dims(…) 함수를 사용하여 단일 차원을 추가하여 벡터를 행렬로 만들어야 한다.
두 번째 함수는 Reward 함수이다. 이진수의 리스트s와 단일 이진수a를 입력받은 다음s의 값이a와 비교해서 얼마나 많은지를 체크한다. 모든 값이 일치하면 Reward는 최대값으로 주어지며, 일치하는 값이 없으면 음수이다. 입력s는 이웃의 List가 된다. 이 경우 가장 가까운 두 개의 이웃을 사용하므로 주어진 에이전트의 경우 이웃이 그리드의 왼쪽 및 오른쪽에있는 에이전트가 된다. 에이전트가 그리드의 끝에 있으면 오른쪽 이웃이 그리드의 첫 번째 요소가 되므로 시작 부분으로 둘러 싼다. 그렇게 해서 그리드를 원형 그리드로 만든다.
Listing 9.4 The 1D Ising Model
def gen_params(N,size): #A
ret = []
for i in range(N):
vec = torch.randn(size) / 10.
vec.requires_grad = True
ret.append(vec)
return ret
#A 신경망에 대한 매개 변수(Parameter) 벡터 List을 생성한다.
신경망을 사용하여 Q-function을 모델링 할 것이기 때문에 이를 위한 매개 변수를 생성해야 한다. 각 에이전트마다 별도의 신경망을 사용하지만 각 에이전트는 동일한 Policy를 가지고 있기 때문에 각 에이전트마다 신경망을 가질 필요는 없으므로 동일한 신경망을 재사용 할 수 있다. 작동 방식을 보여주기 위해 이 함수을 수행하지만 이후 예에서는 동일한 Policy를 가진 에이전트에 대해 공유 Q-function을 사용한다.
1D Ising Model은 매우 단순하기 때문에 PyTorch의 내장 레이어를 사용하지 않고 행렬곱을 하여 신경망을 수동으로 작성한다. State 벡터와 매개 변수 벡터를 받아들이는 Q-function을 만들고 함수 본문에서 매개 변수 벡터를 네트워크의 각 레이어를 만드는 여러 행렬에 Unpack한다.
Listing 9.5 The 1D Ising Model
def qfunc(s,theta,layers=[(4,20),(20,2)],afn=torch.tanh):
l1n = layers[0]
l1s = np.prod(l1n) #A
theta_1 = theta[0:l1s].reshape(l1n) #B
l2n = layers[1]
l2s = np.prod(l2n)
theta_2 = theta[l1s:l2s+l1s].reshape(l2n)
bias = torch.ones((1,theta_1.shape[1]))
l1 = s @ theta_1 + bias #C
l1 = torch.nn.functional.elu(l1)
l2 = afn(l1 @ theta_2) #D
return l2.flatten()
#A `layers` 에서 첫 번째 튜플을 취하고 그 숫자를 곱하여 첫 번째 레이어로 사용할 `theta` 벡터의 부분 집합을 구한다.
#B `theta` 벡터 부분 집합을 신경망의 첫 번째 레이어로 사용하기 위해 행렬로 재구성한다.
#C 첫 번째 레이어 계산이다. `s` 입력은 (4,1) 차원의 Joint Action 벡터이다.
#D 마지막 레이어에 사용할 Activation function을 입력 할 수도 있다. Reward 범위가 [-1,1]이므로 기본값은 tanh이다.
이 함수는 단순히 2계층 신경망으로 구현된 Q-function이다. 이웃 State의 이진수 벡터s와 매개 변수 벡터 theta가 필요하다. 또한 각 레이어에 대한 파라미터 행렬를 나타내는 [(s1, s2), (s3, s4) …] 형식의 List인 키워드 파라미터layers가 필요하다. 일반적인 Q-function과 마찬가지로 이 함수는 가능한 각 Action(이 경우 다운 / 업 (2 동작))에 대한 Q-value를 반환한다. 예를 들어, 스핀을 아래로 변경하는 데 필요한 Reward가 -1이고 스핀을 위로 변경하는 데 필요한 Reward가 +1임을 나타내는 벡터 [-1,1]을 반환 할 수 있다.
단일 매개 변수 벡터를 사용하면 여러 신경망에 대한 모든 매개 변수를 벡터 List으로 쉽게 저장할 수 있으며 신경망에서 벡터를 레이어 행렬로 Unpack할 수 있다. tanh Activation function은 출력이 [-1,1] 간격이고 Reward가 [-2,2] 사이이므로 a + 2 Reward는 Q-value 출력을 +1쪽으로 강하게 밀어내기 때문에 tanh Activation function을 사용한다. 그러나 나중에 프로젝트에서 이 Q-function을 재사용할 수 있기를 원하므로 Activation function를 선택적인 키워드 매개 변수인 ‘afn’으로 제공한다.
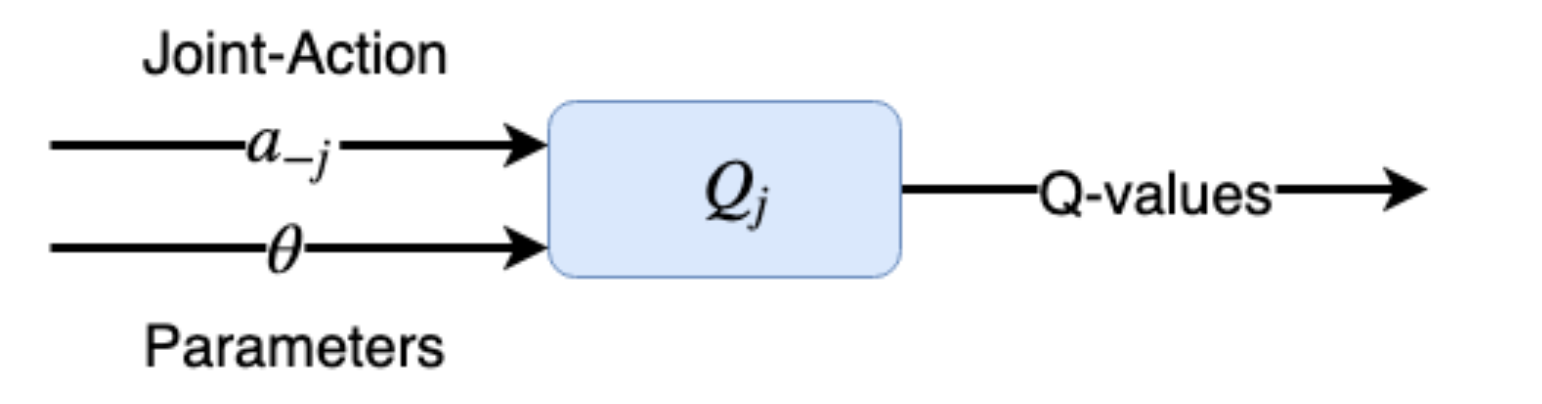
Figure 9.13 에이전트 j의 Q-function은 에이전트 j의 이웃에 대한 매개 변수 벡터와 one-hot 인코딩된 Joint Action 벡터를 받는다.
Listing 9.6 The 1D Ising Model
def get_substate(b): #A
s = torch.zeros(2)
if b > 0: #B
s[1] = 1
else:
s[0] = 1
return s
def joint_state(s): #C
s1_ = get_substate(s[0]) #D
s2_ = get_substate(s[1])
ret = (s1_.reshape(2,1) @ s2_.reshape(1,2)).flatten() #E
return ret
#A 단일 이진수를 입력받아 [0,1]과 같은 one-hot 인코딩된 Action 벡터로 바꾼다.
#B 입력이 0(아래)이면 Action 벡터는 [1,0]이고 그렇지 않으면 [0,1]이다.
#C`s`는 s[0] = 왼쪽 이웃, s[1] = 오른쪽 이웃 인 2개의 요소를 가진 벡터이다.
#D`s`의 각 요소에 대한 Action 벡터를 얻는다
#E 외적을 사용하여 Joint Action space를 만든 후 벡터로 평탄화한다.
Q-function에 대한 State 정보를 준비하는 데 필요한 두 가지 보조 함수이다. get_substate 함수는 단일 이진수(스핀 다운의 경우 0, 스핀 업의 경우 1)를 사용하여 one-hot 인코딩된 Action 벡터로 변환한다. 여기서 [down, up]의 Action space에 따라 0은 [1,0]이 되고 1은 [0,1]이 된다. 그리드에는 각 에이전트의 스핀을 나타내는 일련의 이진수만 포함되고 이 이진수를 Action 벡터로 변환한 후 외적을 사용하여 Q-function에 대한 Joint Action 벡터를 구한다.
Listing 9.7 The 1D Ising Model
plt.figure(figsize=(8,5))
size = (20,) #A
hid_layer = 20 #B
params = gen_params(size[0],4*hid_layer+hid_layer*2) #C
grid = init_grid(size=size)
grid_ = grid.clone() #D
print(grid)
plt.imshow(np.expand_dims(grid,0))
#A 그리드의 총 크기를 20 벡터로 설정
#B 히든 레이어의 크기를 설정한다. Q-function은 2계층 신경망이므로 히든 레이어는 1이다
#C Q-function을 매개 변수화할 매개 변수 벡터 List를 생성한다.
#D Main 학습 루프에서 그리드가 크린(clearn)되므로 해당 그리드 복제본을 만든다.
해당 코드를 실행하면 다음과 같이 표시된다(랜덤으로 초기화 되었기 때문에 여러분의 결과는 다르게 보일 것이다).
tensor([0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0],
dtype=torch.uint8)

Figure 9.14 하나의 열로 배열된 전자의 1D Ising Model.
스핀이 위(1)와 아래(0) 사이에 무작위로 분포되어 있음을 알 수 있다. 우리는 Q-fucntion을 학습시킬 때 스핀이 같은 방향으로 정렬되기를 기대한다. 스핀이 모두 같은 방향으로 정렬 될 수는 없지만, 적어도 모두 정렬된 도메인으로 클러스터링 되어야 한다. 필요한 함수를 모두 정의 했으므로 이제 학습 과정을 시작하겠다.
Listing 9.8 The 1D Ising Model
epochs = 200
lr = 0.001 #A
losses = [[] for i in range(size[0])] #B
for i in range(epochs):
for j in range(size[0]): #C
l = j - 1 if j - 1 >= 0 else size[0]-1 #D
r = j + 1 if j + 1 < size[0] else 0 #E
state_ = grid[[l,r]] #F
state = joint_state(state_) #G
qvals = qfunc(state.float().detach(),params[j],layers=[(4,hid_layer),(hid_layer,2)])
qmax = torch.argmax(qvals,dim=0).detach().item() #H
action = int(qmax)
grid_[j] = action #I
reward = get_reward(state_.detach(),action)
with torch.no_grad(): #J
target = qvals.clone()
target[action] = reward
loss = torch.sum(torch.pow(qvals - target,2))
losses[j].append(loss.detach().numpy())
loss.backward()
with torch.no_grad(): #K
params[j] = params[j] - lr * params[j].grad
params[j].requires_grad = True
with torch.no_grad(): #L
grid.data = grid_.data
#A Learning rate
#B 각각 별도의 Q-function으로 제어되는 여러 에이전트를 다루기 때문에 여러 손실을 추적해야 한다.
#C 각 에이전트를 반복
#D 처음에 왼쪽 이웃을 얻는다.
#E 오른쪽 이웃을 얻는다. 현재 에이전트가 루프의 끝 지점에 있으면 오른쪽 이웃은 루프의 시작 지점이 된다.
#F state_는 왼쪽 및 오른쪽 이웃의 스핀을 나타내는 두 개의 이진수이다.
#G state_는 두 Agent의 Action을 나타내는 두 개의 이진수로 구성된 벡터이다.
#H Policy은 가장 높은 Q-value와 관련된 Action를 취하는 것이다.
#I 임시 그리드인`grid_`에서만 Action를 취하며 모든 에이전트가 Action를 취한 후에만 임시그리드로부터 `grid`에 복사한다.
#J Target value는 수행한 Action과 관련된 Q-value가 관찰된 Reward로 대체된 Q-value 벡터이다.
#K 수동으로 gradient descent 한다.
#L 임시`grid_`의 내용을 `grid` 벡터로 복사한다.
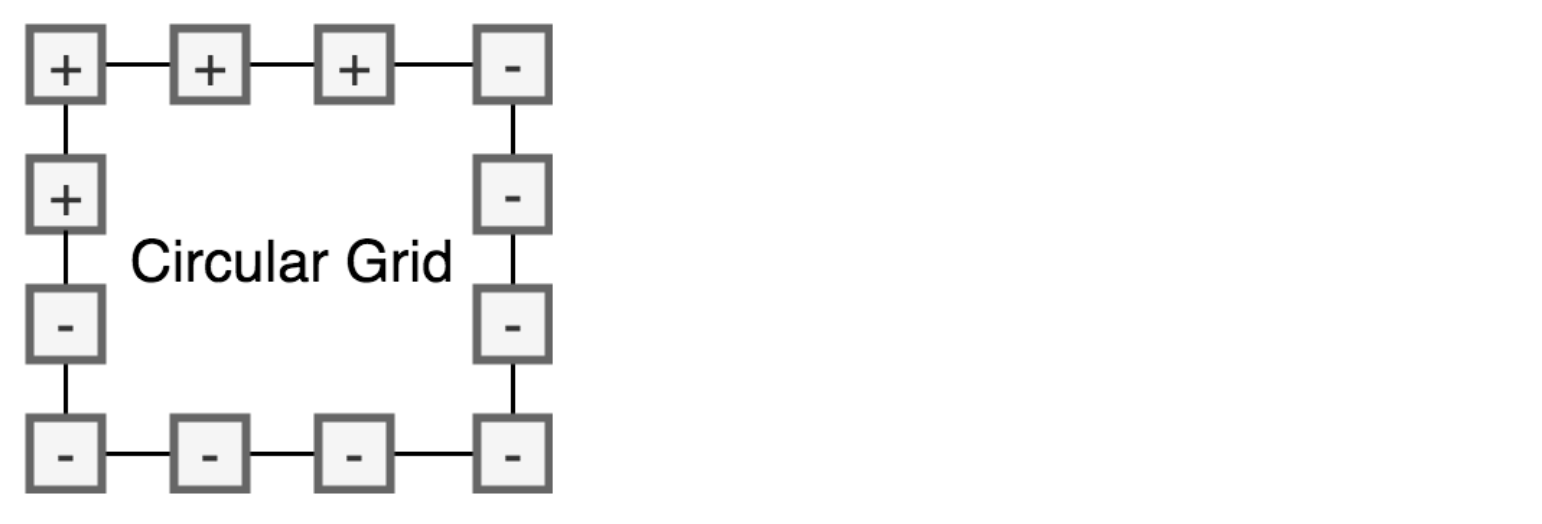
Figure 9.15 단일 이진 벡터로 1D Ising 모델을 나타낼 때, 가장 왼쪽 전자를 가장 오른쪽 전자 바로 옆에있는 것으로 취급하기 때문에 실제로는 Circular Grid로 표현된다.
Main 학습 루프에서, 20개의 에이전트(전자를 나타내는)를 반복하여 각각의 왼쪽 및 오른쪽 이웃을 찾고 그들의 Joint Action 벡터를 얻고 이 벡터를 사용하여 두 가지 가능한 Action에 대한 Q-value을 계산한다. 스핀 다운 및 스핀 업. 각 에이전트에는 Q-function을 매개 변수화하는 데 사용하는 자체 관련 매개 변수 벡터가 있으므로 각 에이전트는 별도의 Deep Q-network 에 의해 제어된다(2 계층 신경망이므로 실제로 그렇게 깊지 않음). 다시 말하지만, 각 에이전트는 동일한 Optimal Policy를 가지고 있고 이웃과 동일한 방식으로 조정해야하기 때문에 실제로는 단일 DQN만을 사용하여 모든 에이전트를 제어해야 한다. 후속 프로젝트에서 이런 접근 방식을 사용할 것이지만 각 에이전트를 개별적으로 모델링하는 것이 얼마나 간단한지를 보여주는 것이 유용하다고 생각했다. 각 에이전트가 다른 Optimal Policy를 가질 수 있는 다른 환경에서는 각각에 대해 별도의 DQN을 사용해야 한다.
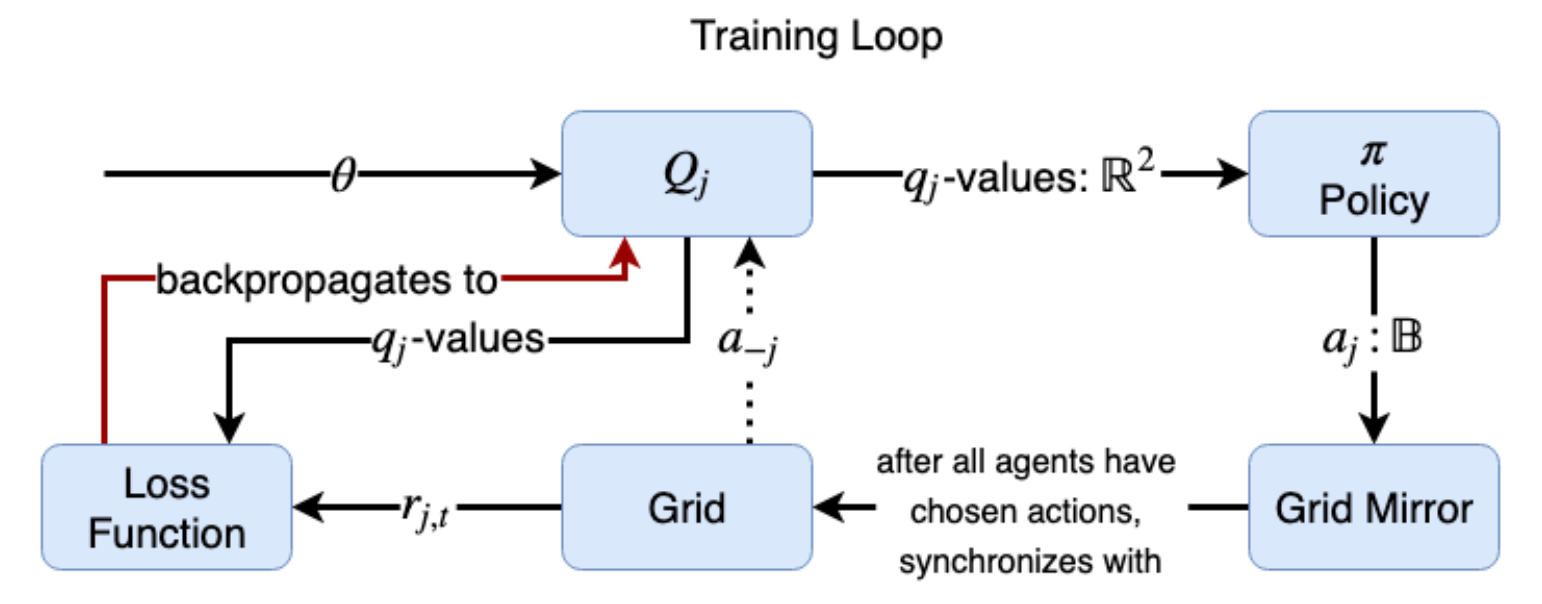
그림 9.16 Main 학습 루프의 문자열 다이어그램. 각각의 에이전트 j에 대해, 대응하는 Q-function은 a-j로 표시된 에이전트에 대한 파라미터 벡터 와 Joint Action 벡터를 취한다. Q-function은 Policy 함수에 입력되는 2요소 Q-value 벡터를 출력한다.이 함수는 Action(2진수)을 선택한 다음 그리드 환경의 미러(복제)에 저장된다. 모든 에이전트가 Action을 선택한 후 미러 그리드는 기본 그리드와 동기화된다. Reward는 각 에이전트에 대해 생성되고 손실 함수로 전달된다. 손실 함수는 손실을 계산하고 손실을 Q-function으로 역전파하고 파라미터 업데이트를 위해 매개 변수 벡터로 역전파한다.
혼란을 피하기 위해 Main 학습 함수를 약간 단순화했는데 문제가 간단하기 때문에 괜찮다. 우선 필요로 하는 Policy는 Greedy Policy이다. 에이전트는 매번 Q-value가 가장 높은 Action을 수행하며, 때때로 임의의 Action을 수행하는 Epsilon-Greedy Policy는 없다. 일반적으로 일종의 탐험 전략이 필요하지만 이 문제가 간단한 문제여서 탐험 전략이 없어서도 동작한다. 다음 섹션에서는 정사각형 그리드에서 2 차원 Ising 모델을 풀고,이 경우 온도 매개 변수가 모델링하려는 전자 시스템의 실제 물리적 온도를 모델링하는 softmax Policy을 사용한다. 또 다른 단순화는 Target Q-value가 rt + 1 + γ * V (st + 1)가 아닌 rt + 1 (동작을 수행 한 후의 Reward)으로 만 설정된다는 것입니다. 마지막 항은 Action를 취한 후의 할인 계수 감마에 State-value를 곱한 값니다. V(st + 1)는 후속 State st + 1의 최대 Q-value을 취하여 계산된다. 이것은 우리가 DQN 장에서 배운 부트스트랩 항이다. 이 항를 나중에 2D Ising Model에 포함시킬 것이다.
학습 루프를 실행하고 그리드를 다시 시각화하면 다음과 같이 표시된다.
>>> fig,ax = plt.subplots(2,1)
>>> for i in range(size[0]):
ax[0].scatter(np.arange(len(losses[i])),losses[i])
>>> print(grid,grid.sum())
>>> ax[1].imshow(np.expand_dims(grid,0))
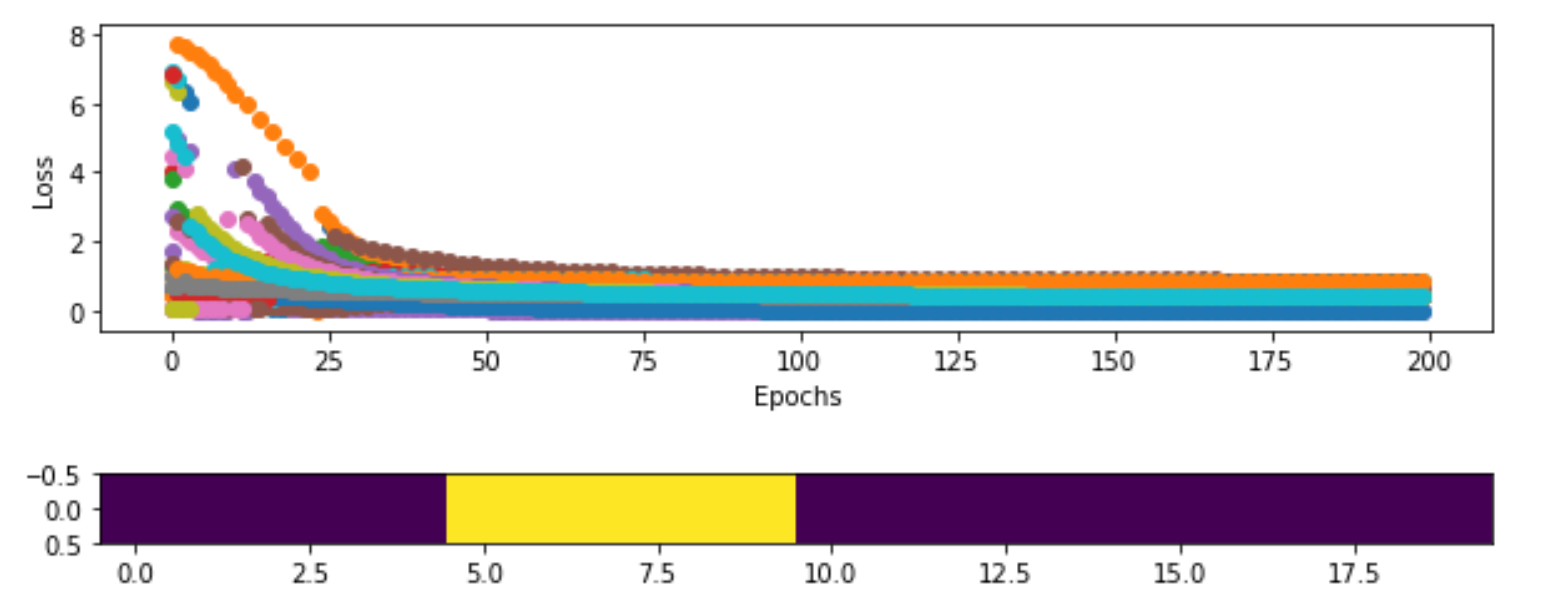
Figure 9.17 상단 : 학습 기간 동안 각 에이전트의 손실. 모든 에이전트들의 손실이 줄어든다는 것을 알 수 있으며 약 30 Epoch 정도 후에는 최소가 된다. 하단 : Reward을 최대화(에너지 최소화) 한 후 1D Ising Model. 모든 전자가 같은 방향으로 향하는 도메인으로 함께 모여있는 것을 볼 수 있다.
첫 번째 시각화는 각 에이전트에 대한 각 Epoch에서의 손실에 대한 산점도(Scatter Plot)이다(각 색상은 다른 에이전트를 말한다). 약 50 Epoch 근처에서 손실이 감소하다 안정기 상태를 보여 준다. 하단 플롯은 Ising Model 그리드이며, 서로 완전히 정렬된 두 개의 도메인으로 구성되어 있음을 알 수 있다. 가운데의 밝은 부분은 모두 위쪽(1) 방향으로 정렬된 에이전트 그룹이며 나머지는 모두 아래쪽(0) 방향으로 정렬되어 있다. 처음 시작한 무작위 분포(Random Distribution)보다 훨씬 낫은 것을 볼 때 MARL 알고리즘은 1D Ising model을 해결하는 데 확실히 효과가 있다. 그러면 조금 더 복잡한 2D Ising model로 가 보자. 몇 가지 단순화를 다루는 것 외에도 평균 필드(Mean Field) Q-learning이라는 이웃 Q-learning 에 대한 새로운 접근 방식을 다룰 것이다.
9.4 Mean Field Q-Learning 과 2D Ising Model
이웃 Q-learning 접근법이 어떻게 1D Ising model의 문제를 어떻게 빠르게 해결할 수 있는지 보았다. 이는 2^20 = 1,048,576 개의 요소 Joint Action 벡터인 전체 Joint Action space를 사용하기보다는 각 에이전트의 왼쪽 및 오른쪽 이웃을 사용하여 크기를 2^2 = 4 요소 Joint Action 벡터로 줄였기 때문이다. 이 벡터는 매우 관리하기 쉽다.
2D 그리드에서 동일한 Action을 수행하고 에이전트의 인접 이웃의 Joint Action space를 얻으려면 8개의 이웃이 있으므로 Joint Action space은 2^8 = 256 요소 벡터이다. 256 요소 벡터를 사용한 컴퓨팅은 확실히 가능하지만 20x20 그리드의 400 에이전트는 비용이 많이 들것이다. 3D Ising model을 사용하고자 한다면, 바로 근접한 이웃의 수는 26개이고 Joint Action space은 2^26 = 67,108,864이며 이것은 다루기 힘든 영역이다.
요점은 전체 Joint Action space을 사용하는 것보다 이웃 접근(Neighborhood approach) 방식이 훨씬 낫다는 것이다. 그러나 더 복잡한 환경에서 인접 이웃(Immediate Neighbor) 수가 많을 때 인접 이웃의 Joint Action space 조차 너무 크다. 더 크고 단순화된 근사치를 만들어야 한다. 이웃 접근 방식이 Ising 모델에서 작동하는 이유는 전자의 회전이 가장 가까운 이웃의 자기장에 가장 큰 영향을 받기 때문이다. 자기장 강도는 필드 소스(Field source)로부터의 거리의 제곱에 비례하여 감소하므로 멀리 떨어지 이웃 전자를 무시하는 것은 합리적이다.
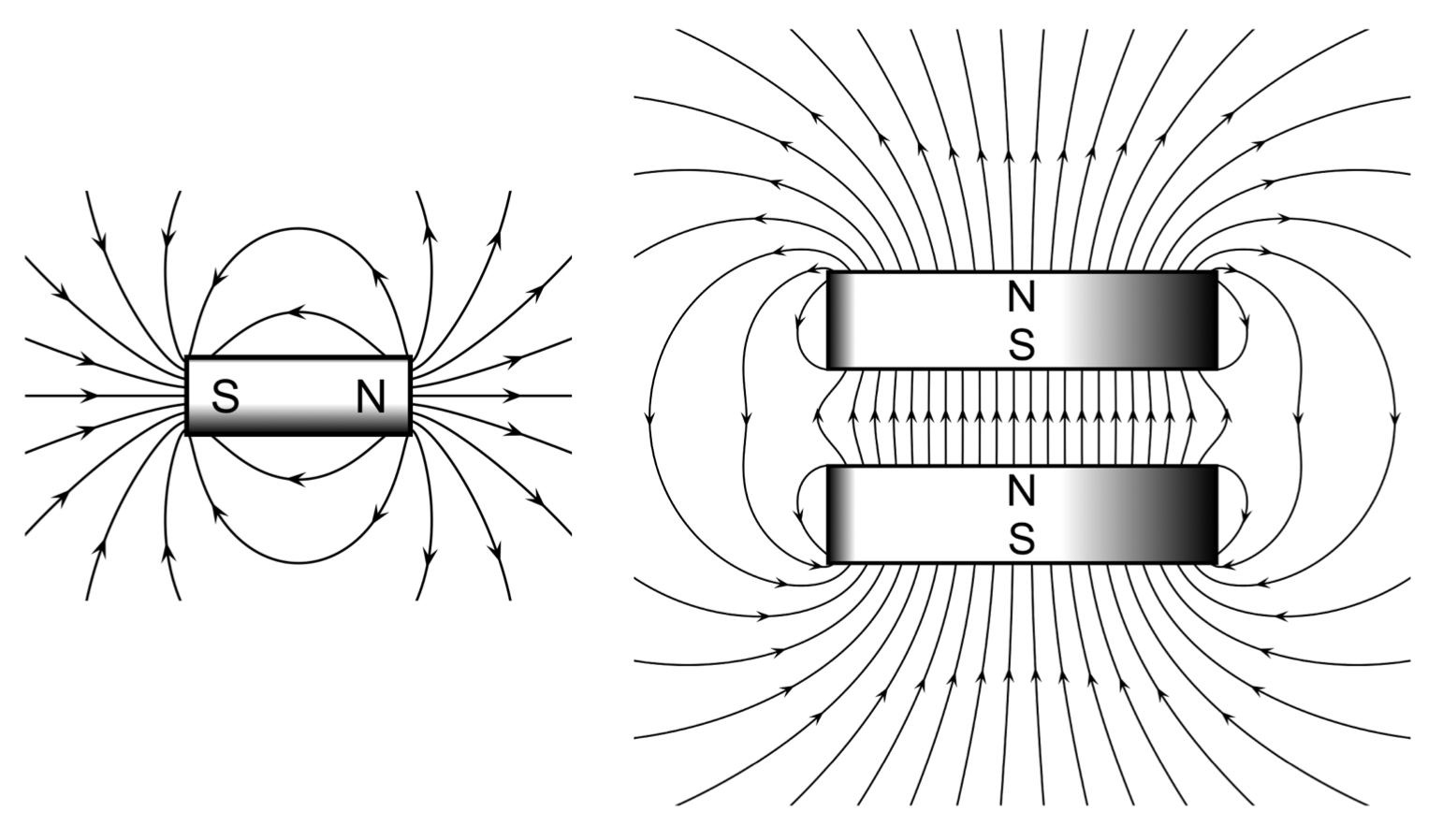
그림 9.18 왼쪽은 단일 막대 자석과 자기장 선이다. 자석은 북쪽(N)과 남쪽(S)이라고 하는 두 개의 자극이 있다. 오른쪽은 두 개의 막대 자석이 가깝게 결합되어 있으며 결합된 자기장의 모습이 조금 더 복잡하다. 2D 또는 3D 그리드에서 전자 스핀이 어떻게 동작하는 지 모델링 할 때, 이웃 전자에 의해 생성된 전체 자기장에 주의해야 한다. 각 전자의 자기장이 무엇인지 알 필요는 없다.
두 개의 자석이 가까이 있을 때 결과 필드(Field, 장)가 이 두 자석의 합(Sum)이라는 점을 이용해서 또 다른 근사를 만들 수 있다. 두 개의 분리된 자석에서 두 자석의 구성 요소의 합인 하나의 자석과 자기장이 있다는 근사치로 대체 할 수 있다. Q-learning에 가장 가까운 각 인접 전자에 대한 스핀 정보를 제공하는 대신, 가장 가까운 인접 전자의 개별 자기장의 합계를 제공한다. 예를 들어, 1D 그리드에서 왼쪽 이웃의 동작 벡터가 1,0이고 오른쪽 이웃의 동작 벡터가 0,1이면 합은 [1, 0] + [0,1] = [1,1] 이다.
머신 러닝 알고리즘은 [0,1]과 같은 고정 범위 내에서 데이터가 정규화 될 때 더 잘 수행된다. 부분적으로는 Activation function이 제한된 출력 범위(공동 도메인) 내에서만 데이터를 출력하고 크거나 작은 입력으로 “포화(saturated)”될 수 있기 때문이다. 예를 들어, tanh 함수는 [-1, + 1] 간격으로 코도메인(codomain, 출력 할 수있는 값의 범위)을 가지므로 실제로는 크지만 같지 않은 두 개의 숫자를 제공하면 숫자가 매우 가깝게 출력된다. 컴퓨터는 정밀도가 제한되어 있기 때문에 입력이 다르더라도 1로 반올림 될 수 있다. 예를 들어 이러한 입력을 [-1,1] 내에 있도록 정규화 한 경우 tanh는 한 입력에 대해 0.5를, 다른 입력에 대해 0.6을 반환 할 수 있다.
따라서 Q-function에 개별 Action 벡터의 합을 제공하는 대신 합을 모든 요소의 총값으로 나눠서 결과 벡터의 요소를 [0,1] 사이로 정규화한다 . 예를 들어 [1,0] + [0,1] = [1,1] / 2 = [0.5,0.5]를 계산한다. 이 정규화된 벡터의 합은 1이되고 각 요소는 [0,1] 사이에 있게 된다. 방금 설명한 것으로 부터 무엇이 떠오르는가? 확률 분포. 정리하자면, 가장 가까운 이웃의 Action에 대한 확률 분포를 계산하고 그 벡터를 Q-function에 제공하는 것이 된다.
평균 필드 Action 벡터 계산하기
일반적으로 아래 공식을 사용하여 평균 필드 Action 벡터를 계산한다.

여기서 a-j는 에이전트 j 주위의 주변 에이전트의 평균 필드에 대한 표기법이고 ai는 에이전트 j의 이웃 중 하나인 에이전트 i의 Action 벡터를 나타낸다. 따라서 에이전트 j에 대해 크기 N의 이웃에 있는 모든 Action 벡터를 합한 다음 정규화할 이웃의 크기로 나눈다. 수학이 잘 이해가 안된다면, 파이썬에서 어떻게 작동하는지 살펴 보자.
이 접근법을 평균 필드 근사(Mean Field Approximation) 또는 평균 필드 Q-learning(MF-Q)이라고 한다. 아이디어는 각 이웃의 모든 개별 자기장을 사용하지 않고 각 전자 주변의 일종의 평균 자기장을 계산하여 사용한다는 것이다. 이 접근 방식의 가장 큰 장점은 평균 필드 벡터가 이웃 크기나 총 에이전트 수에 관계없이 개별 Action 벡터만큼만 길다는 것이다.
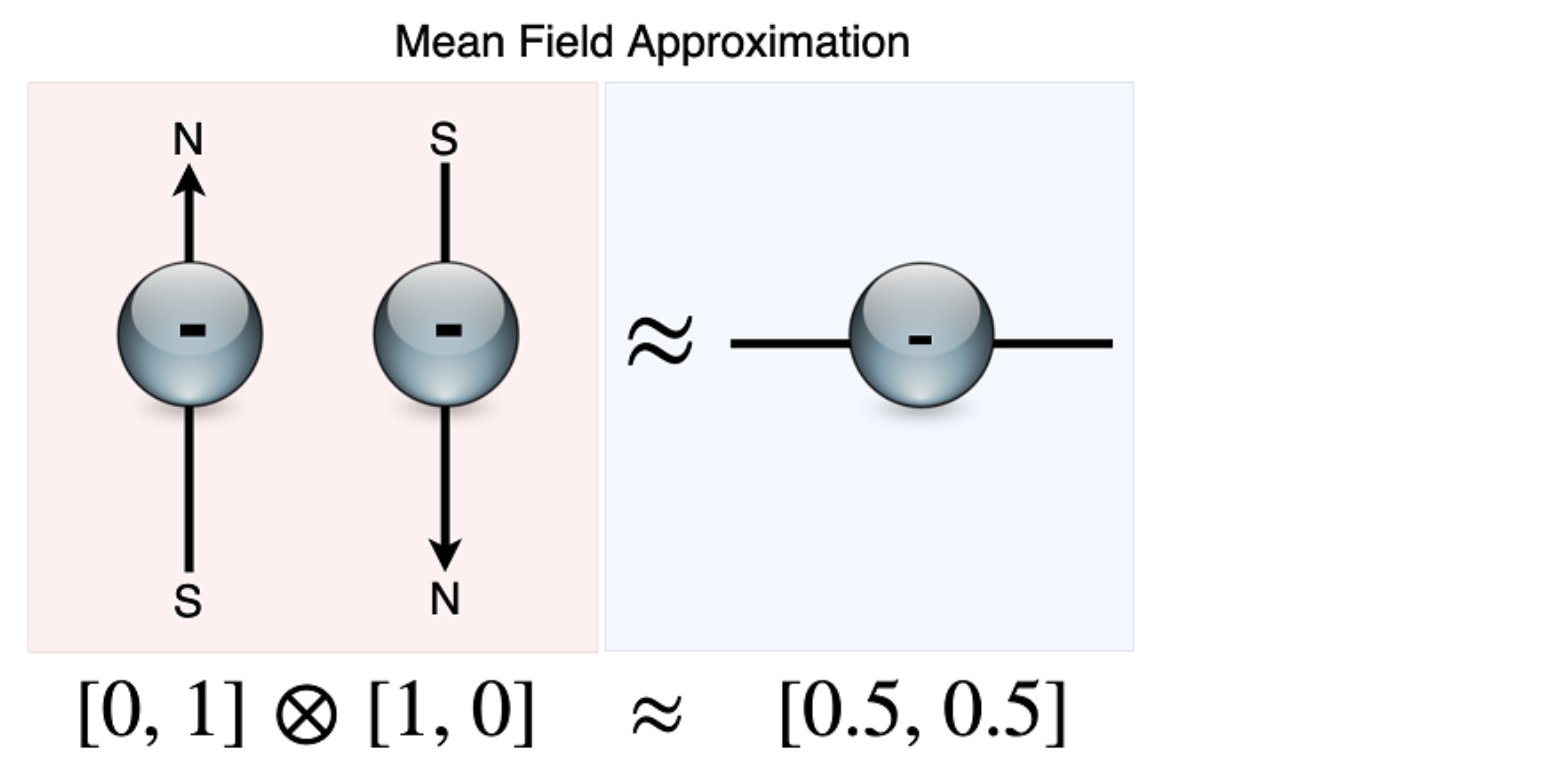
Figure 9.19 한 쌍의 전자 스핀에 대한 Joint Action은 개별 Action 벡터 사이의 외적이며, 이는 4요소 one-hot 벡터이다. 이 정확한 Joint Action을 사용하는 대신이 두 Action 벡터의 평균을 구해 근사치를 계산하여 사용하는데 이를 평균 필드 근사(Mean Field Approximation) 라고 한다. 스핀 업, 스핀 다운과 함께 두 개의 전자에 대해, 평균 필드 근사는 이 두 전자를 [0.5,0.5]의 불확정 스핀을 갖는 단일 “가상” 전자로 줄인다.
즉, 각 에이전트의 평균 필드 벡터는 1D Ising 모델과 2D Ising 모델 및 더 높은 차원의 Ising 모델에 대해서도 2요소 벡터만 있으면 됩니다. 이는 환경이 임의로 복잡하고 고차원적이어도 계산하기 쉽다는 것을 의미한다. 평균 필드 Q-learning(MF-Q)이 2D Ising 모델에서 어떻게 작동하는지 보자. 2D Ising 모델은 2D 그리드 (즉, 행렬)라는 점을 제외하고 1D 버전과 정확히 동일하다. 왼쪽 상단에 있는 에이전트는 왼쪽 이웃이 오른쪽 상단에 있는 에이전트가 되고, 위의 이웃이 왼쪽 하단에 있는 에이전트가 되므로 그리드는 실제로 구의 표면을 감싸는 그리드이다.

Figure 9.20 2D Ising 모델을 2D 정사각형 그리드(예 : 행렬)로 표현하지만 실제로 경계가 없고 경계에 나타나는 에이전트가 실제로 반대쪽 에이전트에 바로 인접하도록 모델을 설계한다. 따라서 2D 그리드는 실제로 구의 표면을 감싸는 2D 그리드이다.
Listing 9.9 Mean Field Q-learning
from collections import deque #A
from random import shuffle #B
def softmax_policy(qvals,temp=0.9): #C
soft = torch.exp(qvals/temp) / torch.sum(torch.exp(qvals/temp)) #D
action = torch.multinomial(soft,1) #E
return action
#A deque 데이터 구조는 최대 크기로 설정 될 수 있으므로 경험 재생 스토리지 목록으로 사용된다.
#B 셔플 기능을 사용하여 경험 재생 버퍼를 셔플링한다.
#C Q-value 벡터를 취하여 0(아래) 또는 1(위)의 Action을 리턴하는 Policy 함수이다.
#D softmax 함수 정의.
#E softmax 함수는 Q-value를 Action에 대한 확률 분포로 변환한다. 확률로 가중된 Action을 무작위로 선택하는 torch.multinomial() 함수를 사용한다.
2D Ising 모델에 사용할 첫 번째 새로운 함수는 softmax 함수이다. Policy 함수에 대한 아이디어를 소개할 때 N-armed bandit 장에서 이미 보았다. Policy 함수는 State space에서 Action space으로의 함수 π : s → A 이다. 즉, State 벡터를 취하고 수행할 Action을 반환한다. Policy Gradient 장에서 신경망을 Policy function으로 사용하고 최선의 Action를 출력하도록 직접 학습했다. Q-learning에서는 주어진 State에 대해 먼저 Action-value(Q-value)을 계산하는 중간 단계를 가지고 있으며, 그 Action-value을 사용하여 어떤 Action을 취할 것인지 결정한다. Q-learning에서의 Policy 함수는 Q-value을 가져 와서 Action를 반환한다.
SOFTMAX FUNCTION

Pt(a)는 Action에 대한 확률 분포이고, qt(a)는 Q-value 벡터이며 τ는 온도(temperature) 매개 변수이다.
다시 말해, softmax 함수는 임의의 숫자가 포함된 벡터를 가져온 다음이 벡터를 확률 분포로 “정규화”하여 모든 요소가 양수이고 합이 1이 되도록 변환한 후의 각 요소가 이전 요소에 비례하도록 변형한다(즉, 요소가 벡터에서 가장 큰 경우 가장 큰 확률이 할당된다). softmax 함수안에는 그리스 기호 tau τ로 표시된 하나의 추가 입력인 온도(temperature) 매개 변수가 있다.
온도 매개 변수가 크면 요소 간 확률의 차이가 최소화되고 온도 매개 변수가 작으면 입력의 차이가 확대된다. 예를 들어, 벡터 softmax ([10,5,90], temp = 100) = [0.2394, 0.2277, 0.5328] 와 softmax ([10,5,90], temp = 0.1) = [0.0616, 0.0521, 0.8863] 를 보자. 높은 온도에서, 마직막 요소(90)가 두번째 최대 요소(10)보다 9 배 더 크더라도, 결과적인 확률 분포는 0.53의 확률을 부여하는데, 이는 두번째 최대 확률의 약 2배에 불과하다. 온도가 무한대에 도달하면 확률 분포는 균일하게 된다(즉, 모든 확률이 동일하게 됨). 온도가 0에 가까워지면 확률 분포는 모든 확률 질량(Probability Mass)이 단일 지점에 있는 퇴화 분포(Degenerate Distribution)가 된다. 따라서 이를 Policy 함수로 사용하면 τ → ∞ 동작이 완전히 무작위로 선택되고 τ → 0이면 Policy가 argmax 함수가 된다(이전 섹션에서 1D Ising 모델에 사용되었음).
이 매개 변수를 “온도”라고 하는 이유는 softmax 함수가 물리학에서 사용되었기 때문인데, 온도가 시스템의 동작을 변경하는 전자 시스템의 스핀과 같은 물리적 시스템을 모델링하는 데에도 사용되기 때문이다. 물리학과 기계 학습 사이에는 많은 교류(cross-pollination)가 있다. 물리학에서 볼츠만 분포 (Boltzmann Distribution)라고 불불리는 데 “시스템이 해당 상태의 에너지와 시스템 온도에 따라 특정 상태에 있을 확률을 제공한다”(Wikipedia). 일부 강화 학습 학술 논문에서는 Boltzmann Policy라는 이름으로 softmax Policy을 볼 수 있는데 이것은 서로 동일한 내용임을 알 수 있다.
물리학 문제를 해결하기 위해 강화 학습 알고리즘을 사용하고 있기 때문에 softmax 함수의 온도 매개 변수는 실제로 모델링하는 전자 시스템의 온도와 일치한다. 시스템의 온도를 매우 높게 설정하면 전자가 무작위로 회전하고 이웃에 정렬되는 경향이 낮아진다. 온도를 너무 낮게 설정하면 전자가 고착되어 크게 변하지 않는다.
Listing 9.10 Mean Field Q-learning
def get_coords(grid,j): #A
x = int(np.floor(j / grid.shape[0])) #B
y = int(j - x * grid.shape[0]) #C
return x,y
def get_reward_2d(action,action_mean): #D
r = (action*(action_mean-action/2)).sum()/action.sum() #E
return torch.tanh(5 * r) #F
#A 평탄화된 그리드에서 단일 인덱스 값을 가져와 [x, y]좌표로 다시 변환한다.
#B x 좌표 찾기
#C y 좌표 찾기
#D 2D 그리드에 대한 Reward 함수이다.
#E Reward는 Action이 평균 필드 Action과 얼마나 다른지에 따라 결정된다.
#F tanh 함수를 사용하여 Reward를 [-1, + 1] 사이로 조정한다.
[x, y] 좌표를 사용하여 2D 그리드의 에이전트를 참조하는 것은 불편하므로 일반적으로 2D 그리드를 벡터로 평탄화하여 이를 보고 단일 인덱스 값을 사용하는 에이전트를 참조한다. 이 때 평탄한 인덱스를 [x, y] 좌표로 변환 할 수 있어야 한다. 이 때 사용하는 것이 get_coords 함수이다. get_reward_2d 함수는 2D 그리드에 대한 새로운 Reward 함수이다. Action 벡터와 평균 필드 벡터의 차이를 계산한다. 예를 들어 평균 필드 벡터가 [0.25,0.75]이고 Action 벡터가 [1,0] 인 경우 Action 벡터가 [0,1] 인 경우보다 Reward가 낮아야 한다.
>>> get_reward_2d(torch.Tensor([1,0]),torch.Tensor([0.25, 0.75]))
tensor(-0.8483)
>>> get_reward_2d(torch.Tensor([0,1]),torch.Tensor([0.25, 0.75]))
tensor(0.8483)
이제 에이전트의 가장 가까운 이웃을 찾은 다음 이 이웃에 대한 평균 필드 벡터를 계산하는 함수를 만들어야 한다.
Listing 9.11 Mean Field Q-learning
def mean_action(grid,j):
x,y = get_coords(grid,j) #A
action_mean = torch.zeros(2) #B
for i in [-1,0,1]: #C
for k in [-1,0,1]:
if i == k == 0:
continue
x_,y_ = x + i, y + k
x_ = x_ if x_ >= 0 else grid.shape[0] - 1
y_ = y_ if y_ >= 0 else grid.shape[1] - 1
x_ = x_ if x_ < grid.shape[0] else 0
y_ = y_ if y_ < grid.shape[1] else 0
cur_n = grid[x_,y_]
s = get_substate(cur_n) #D
action_mean += s
action_mean /= action_mean.sum() #E
return action_mean
#A 벡터화된 인덱스 j를 그리드 좌표 [x, y]로 변환한다. 여기서 [0,0]은 왼쪽 상단이다.
#B 추가할 Action 평균 벡터가 된다.
#C 두 개의 for 루프를 돌면서 에이전트 `j`의 가장 가까운 8개의 이웃을 각각 찾을 수 있다.
#D 각 이웃의 이진 스핀을 Action 벡터로 변환한다.
#E Action 분포를 확률 분포로 정규화한다.
이 함수는 에이전트 인덱스j (단일 정수, 평탄화된 그리드를 기반으로하는 인덱스)를 취하고 그리드에서 에이전트의 가장 가까운 (주변)이웃의 평균 Action을 반환한다. 예를 들어 [5,5]와 같은 에이전트의 좌표를 가져와 가장 가까운 8개의 이웃을 찾은 다음 x, y∈ {0,1}에 [x, y]의 모든 조합(combination)을 추가한다. 따라서 [5,5] + [1,0] = [6,5] 와 [5,5] + [-1,1] = [4,6] 등을 수행한다.
이 함수들은 2D Ising 모델을 처리하기 위해 필요한 추가 함수들이다. 이전의init_grid 함수와 gen_params함수를 재사용 할 것이다. 그러면 그리드와 매개 변수를 초기화하자.
>>> size = (10,10)
>>> J = np.prod(size)
>>> hid_layer = 10
>>> layers = [(2,hid_layer),(hid_layer,2)]
>>> params = gen_params(1,2*hid_layer+hid_layer*2)
>>> grid = init_grid(size=size)
>>> grid_ = grid.clone()
>>> grid__ = grid.clone()
>>> plt.imshow(grid)
>>> print(grid.sum())

Figure 9.21 무작위로 초기화된 2D Ising 모델이다. 각 격자 사각형은 전자를 나타낸다. 밝은 색의 격자 사각형은 스핀“위”로 향한 전자를 나타내고 어두운 사각형은 스핀“아래”를 나타낸다.
빠른 실행을 위해 10x10 그리드로 시작하지만 더 큰 그리드 크기로 실험해 봐야 한다. 스핀이 초기 그리드에 무작위로 분포되어 있지만, 이후 MARL 알고리즘을 실행하면 그리드가 훨씬 체계적으로 바뀌어서 보일 것이다. 즉, 정렬된 전자 클러스터를 볼 수 있게 된다. 컴퓨팅 비용을 줄이기 위해 추가적으로 숨겨진 레이어 크기를 10으로 줄였다. 하나의 매개 변수 벡터만 생성하므로 100개의 에이전트가 동일한 Optimal Policy를 갖기 때문에 단일 DQN을 사용하여 모든 에이전트를 제어 할 것이다. 학습 루프에 도달하면 그리드를 Clear해야 하므로 두 개의 grid 사본을 만든다.
이 예제에서는 약간 더 어려운 문제를 만들기 위해 1D Ising 모델 사례에서 제외했던 몇 가지 복잡성을 추가 할 것이다. Experience Replay 메커니즘을 사용하여 경험을 저장하고 이러한 경험의 minibatch를 학습시킬 것이고 이것이 그래디언트의 변화를 줄이고 학습을 안정화시킬 것이다. 또한 적절한 Target Q-value를 사용할 것이다 : rt + 1 + γ * V(st + 1), Iteration을 반복 할 때마다 두 번 Q-value을 계산해야 한다. 첫번째는 어떤 Action을 취해야 하는지 알아내기 위해서, 두번째는 V(st + 1)를 얻기내기 위해서이다.
Listing 9.12 Mean Field Q-learning
epochs = 75
lr = 0.0001
num_iter = 3 #A
losses = [ [] for i in range(size[0])] #B
replay_size = 50 #C
replay = deque(maxlen=replay_size) #D
batch_size = 10 #E
gamma = 0.9 #F
losses = [[] for i in range(J)]
for i in range(epochs):
act_means = torch.zeros((J,2)) #G
q_next = torch.zeros(J) #H
for m in range(num_iter): #I
for j in range(J): #J
action_mean = mean_action(grid_,j).detach()
act_means[j] = action_mean.clone()
qvals = qfunc(action_mean.detach(),params[0],layers=layers)
action = softmax_policy(qvals.detach(),temp=0.5)
grid__[get_coords(grid_,j)] = action
q_next[j] = torch.max(qvals).detach()
grid_.data = grid__.data
grid.data = grid_.data
actions = torch.stack([get_substate(a.item()) for a in grid.flatten()])
rewards = torch.stack([get_reward_2d(actions[j],act_means[j]) for j in range(J)])
exp = (actions,rewards,act_means,q_next) #K
replay.append(exp)
shuffle(replay)
if len(replay) > batch_size: #L
ids = np.random.randint(low=0,high=len(replay),size=batch_size) #M
exps = [replay[idx] for idx in ids]
for j in range(J):
jacts = torch.stack([ex[0][j] for ex in exps]).detach()
jrewards = torch.stack([ex[1][j] for ex in exps]).detach()
jmeans = torch.stack([ex[2][j] for ex in exps]).detach()
vs = torch.stack([ex[3][j] for ex in exps]).detach()
qvals = torch.stack([ qfunc(jmeans[h].detach(),params[0],layers=layers) \
for h in range(batch_size)])
target = qvals.clone().detach()
target[:,torch.argmax(jacts,dim=1)] = jrewards + gamma * vs
loss = torch.sum(torch.pow(qvals - target.detach(),2))
losses[j].append(loss.item())
loss.backward()
with torch.no_grad():
params[0] = params[0] - lr * params[0].grad
params[0].requires_grad = True
#A `num_iter`는 평균 필드 액션에서 초기 임의성을 제거하기 위해 반복하는 횟수를 제어한다.
#B 각 에이전트의 손실을 저장하기 위한 List를 작성한다.
#C`replay_size`는 Experience Replay Lost에 저장하는 총 경험 수를 제어한다.
#D Experience Replay 는 기본적으로 최대 크기를 가진 List 인 deque collection이다.
#E Batch size를 10으로 설정했다. Replay Buffer에서 무작위로 10개의 경험을 취한다.
#F Discount Factor
#G 모든 에이전트의 평균 필드 Action을 저장한다.
#H Action를 취한 후 다음 State의 Q-value을 저장한다.
#I 평균 필드는 무작위로 초기화되므로 초기 무작위성을 희석하기 위해 몇 번 반복해야 한다.
#J 그리드의 모든 에이전트를 반복한다.
#K 경험을 수집하고 Experience Replay Buffer에 추가한다.
#L Experience Replay Buffer에 Batch size 매개 변수보다 더 많은 경험이 있으면 학습을 시작한다.
#M Replay Buffer를 subset하기 위해 Random 인덱스 List를 생성한다.
코드가 많지만 1D Ising 모델에 비해 약간 더 복잡하다. 가장 먼저 보이는 것은 각 에이전트의 평균 필드가 인접 에이전트에 의존하고 인접 스핀이 무작위로 초기화되므로 모든 평균 필드가 무작위로 시작한다는 것이다. 수렴을 돕기 위해 먼저 각 에이전트가 임의의 평균 필드를 기반으로 작업을 선택하고 임시 그리드 사본grid__에 작업을 저장하여 모든 에이전트가 어떤 Action을 취할지 최종 결정을 내릴 때까지 기본 그리드가 변경되지 않도록 한다. 각 에이전트가 grid__에서 잠정 Action를 취한 후 평균 필드를 계산하는 데 사용하는 두 번째 임시 그리드 사본 인 grid_를 업데이트 한다. 따라서 다음 반복에서 평균 필드가 변경되고 에이전트가 잠정 Action을 업데이트 할 수 있다. 현재 버전의 Q-function에 따라 거의 최적의 값으로 Action을 안정화시킬 수 있도록 몇 번에 걸쳐 이 작업을 반복한다(num_iter 파라미터로 제어). 그런 다음 기본 grid를 업데이트하고 모든 Action, Reward, 평균 필드 및q_next 값(V(st + 1))을 수집하여 Experience Replay Buffer에 추가한다.
Replay Buffer에 Batch size 매개 변수보다 많은 경험이 있으면 재생 버퍼에서 경험의 미니 배치에 대한 학습을 시작할 수 있다. 랜덤 인덱스 값의 List를 생성한 다음 이를 사용하여 Replay Buffer에서 임의의 경험을 subset한다. 그런 다음 Gradient Descent 한 단계를 실행한다. 학습 루프를 실행하고 결과를 보자.
>>> fig,ax = plt.subplots(2,1)
>>> ax[0].plot(np.array(losses).mean(axis=0))
>>> ax[1].imshow(grid)
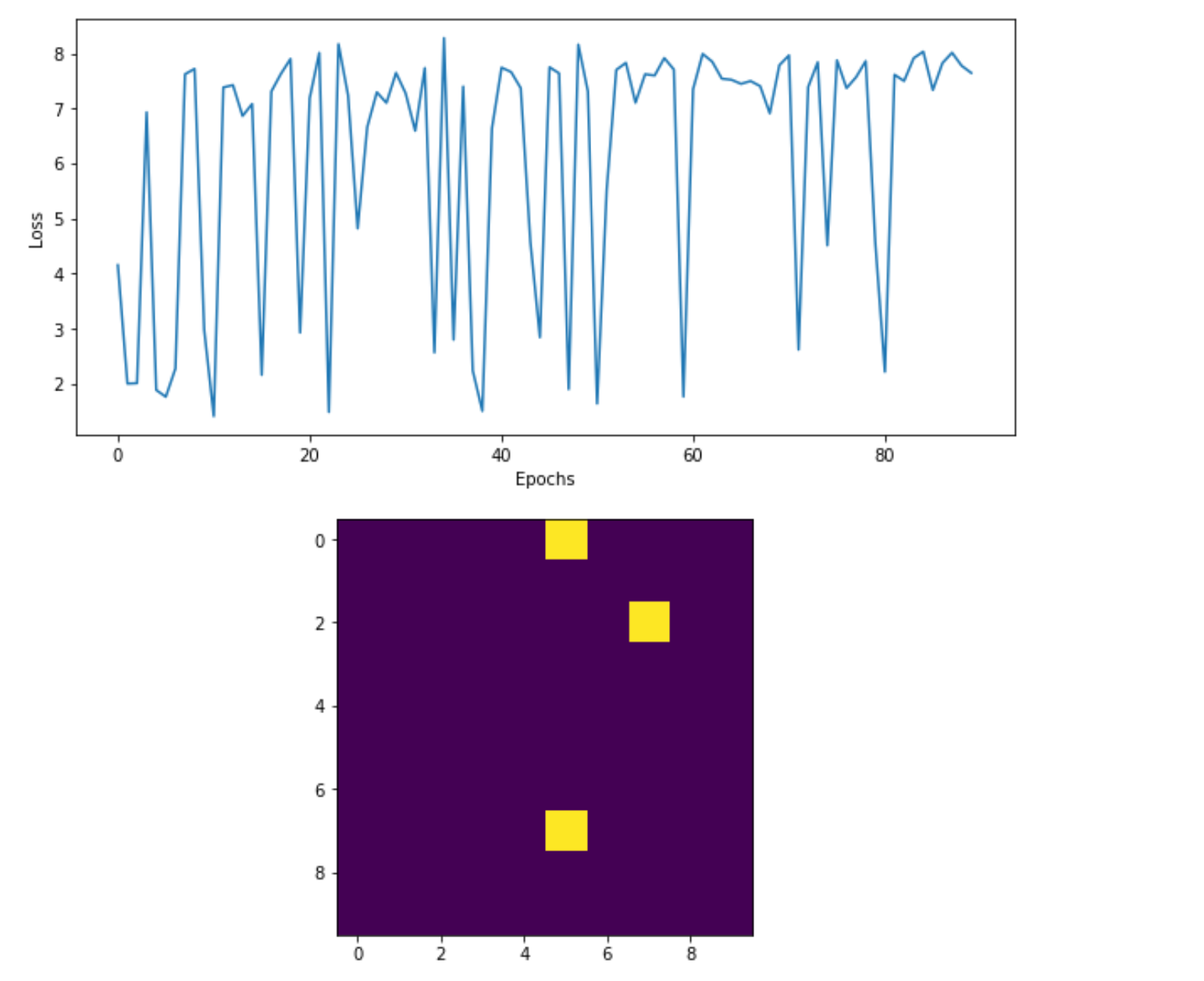
Figure 9.22 상단 : DQN에 대한 손실 플롯. 손실이 수렴하는 것처럼 보이지 않지만 실제로는 하단 패널에서 전체적으로 시스템의 에너지를 최소화(Reward 극대화)하는 방법을 배우고 있음을 알 수 있다.
효과가 있군요! 3개의 전자(에이전트)를 제외한 모든 전자의 스핀은 같은 방향으로 정렬되어 시스템의 에너지를 최소화하고 Reward를 극대화한다. 손실 플롯은 현재 각 에이전트를 모델링하기 위해 단일 DQN을 사용하기 때문에 부분적으로 무질서해 보입니다. 따라서 한 에이전트가 이웃과 정렬하려고 하지만 그 이웃은 다른 에이전트와 정렬하려고 한다. 이 경우 DQN은 자신과의 의사결정에 있어서 싸우는 꼴이되어 에이전트가 약간 불안정 해진다.
마지막 섹션에서 우리는 멀티 에이전트 강화 학습 기술을 게임에서 서로 대항하는 두 팀의 에이전트와 함께 더 어려운 문제를 해결함으로써 다음 단계로 나아가겠다.
9.5 혼합 협동-경쟁 게임(Mixed Cooperative-Competitive Games)
Ising Model을 멀티 플레이어 게임이라고 생각하면 모든 에이전트가 동일한 목표를 가지고 있으며 동일한 방향으로 모든 정렬을 위해 함께 일할 때 보상이 극대화되므로 순수한 협동 멀티 플레이어 게임으로 간주된다. 한 플레이어가 이기고 다른 플레이어가 지는 경우, 즉 제로섬(Zero-Sum) 게임인 체스와 같은 순수한 경쟁 게임을 상상할 수 있다. 같은 팀의 에이전트가 Reward를 극대화하기 위해 협력해야하기 때문에 농구 또는 축구 게임과 같은 팀 기반 게임을 혼합 협동-경쟁 게임(Mixed Cooperative-Competitive Games)이라고 한다. 그러나 전체 팀이 승리하면 다른 팀이 패배해야 하기 때문에 팀 간 수준에서는 경쟁 게임이다.
이 섹션에서는 협력, 경쟁 또는 혼합 협력-경쟁 시나리오에서 멀티 에이전트 강화 학습 알고리즘을 테스트하기 위해 특별히 설계된 오픈 소스 Gridworld 기반 게임을 사용한다. 이 경우 그리드에서 움직일 수 있고 상대 팀의 다른 에이전트를 공격 할 수 있게 되는데, 두 개의 Gridworld 에이전트 팀으로 혼합된 협동-경쟁 시나리오를 설정한다. 각 에이전트는 1 “HP(health point)”로 시작하며 공격을 받으면 HP는 0이 될 때까지 조금씩 줄어든 다음 에이전트가 죽고 그리드에서 제거된다. 에이전트는 상대 팀의 에이전트를 공격하고 죽이는 것에 대한 Reward를 받는다.

Figure 9.24 두 개의 서로 다른 Gridworld 에이전트 팀이 있는 MAgent 멀티 플레이어 Gridworld 게임의 스크린 샷. 목표는 각 팀이 다른 팀을 죽이는 것이다.


한 팀의 모든 에이전트가 동일한 목표와 Optimal Policy를 공유했으므로 단일 DQN을 사용하여 한 팀의 모든 에이전트를 제어하고 다른 DQN을 사용하여 다른 팀의 에이전트를 제어 할 수 있다. 기본적으로 두 DQN 간의 싸움이므로 다양한 종류의 신경망을 시험해보고 어느 것이 더 좋은지 알 수있는 완벽한 실험이다. 그러나 실험을 단순하게 유지하려면 각 팀에 동일한 DQN을 사용하면 된다.
https://github.com/geek-ai/MAgent 에서 readme 페이지의 지침에 따라 MAgent 라이브러리를 설치해야 한다. 이 시점에서 해당 라이브러리를 설치했다고 가정하면, 파이썬 환경에서import magent를 성공적으로 실행할 수 있어야만 한다.
Listing 9.13 MAgent 환경 만들기
import magent
import math
from scipy.spatial.distance import cityblock #A
map_size = 30
env = magent.GridWorld("battle", map_size=map_size) #B
env.set_render_dir("MAgent/build/render") #C
team1, team2 = env.get_handles() #D
#A scipy에서 cityblock distance 함수를 import 하여 그리드에서 에이전트간 거리를 계산한다.
#B 30x30 그리드, "battle" 모드로 환경 설정
#C 학습 후 게임을 Rendering해 볼 수 있도록 설정한다.
#D 두 팀 개체를 초기화한다.
MAgent는 사용자 정의가 가능하지만 “battle”이라는 기본 구성을 사용하여 2팀 전투 시나리오를 설정한다. MAgent에는 OpenAI Gym과 유사한 API가 있지만 몇 가지 중요한 차이점이 있다. 먼저 두 팀 각각에 대해 “핸들(handle)”을 설정해야 한다. 핸들은 각 팀과 관련된 메소드와 속성을 가진team1과team2 객체이다. 일반적으로 이 핸들을 환경 객체env의 메소드에 전달하여 사용한다. 예를 들어, 팀1에서 각 에이전트의 좌표 목록을 얻으려면env.get_pos(team1)을 사용한다다.
2개의 DQN을 사용하는 것을 제외하고는 2D Ising Model에서 했던 것과 동일한 기술을 사용하여 이 환경을 해결한다. 우리는 softmax Policy와 Experience Replay Buffer를 사용할 것이다. 에이전트가 죽으면 그리드에서 제거되기 때문에 에이전트의 수가 학습이 진행됨에 따라 변경되므로 상황이 약간 복잡해진다. Ising Model을 사용하면 환경의 State가 Joint Action이었고 추가 State 정보는 없었다.
MAgent에는 State 정보로 에이전트의 위치(position) 및 HP(health point)가 추가된다. 따라서 Q-function은 Qj(st, a-j)이다. 여기서 a-j는 에이전트 j의 시야(FOV, field of view) 또는 주변에 있는 에이전트의 평균 필드이다. 기본적으로 각 에이전트는 13×13 그리드의 FOV를 가지고 있다. 따라서 각 에이전트는 이진 13x13 FOV 그리드의 State를 가지며 다른 에이전트가 있는 경우 1을 표시한다. 그러나 MAgent는 팀별로 FOV 매트릭스를 분리하므로 각 에이전트에는 고유한 팀과 다른 팀을 위한 두 개의 13x13 FOV 그리드가 있다. 따라서 이를 평탄화(flattening) 및 연결(concatenaing)하여 단일 State 벡터로 결합(combine)해야 한다. MAgent는 또한 FOV에서 에이전트의 HP(health point)을 제공하지만 문제를 단순하게 하기 위해 이 실험에서는 사용하지 않는다.
여기까지 환경을 초기화했지만 그리드에서 에이전트를 초기화하지는 않았다. 각 팀의 에이전트 수와 그리드에 배치할 위치를 결정해야 한다.
Listing 9.14 에이전트 추가하기
hid_layer = 25
in_size = 359
act_space = 21
layers = [(in_size,hid_layer),(hid_layer,act_space)]
params = gen_params(2,in_size*hid_layer+hid_layer*act_space) #A
map_size = 30
width = height = map_size
n1 = n2 = 16 #B
gap = 1 #C
epochs = 100
replay_size = 70
batch_size = 25
side1 = int(math.sqrt(n1)) * 2
pos1 = []
for x in range(width//2 - gap - side1, width//2 - gap - side1 + side1, 2): #D
for y in range((height - side1)//2, (height - side1)//2 + side1, 2):
pos1.append([x, y, 0])
side2 = int(math.sqrt(n2)) * 2
pos2 = []
for x in range(width//2 + gap, width//2 + gap + side2, 2): #E
for y in range((height - side2)//2, (height - side2)//2 + side2, 2):
pos2.append([x, y, 0])
env.reset()
env.add_agents(team1, method="custom", pos=pos1) #F
env.add_agents(team2, method="custom", pos=pos2)
#A 두 개의 파라미터 벡터를 생성하여 두 개의 DQN의 파라미터를 설정한다.
#B 각 팀의 에이전트 수를 16으로 설정한다.
#C 각 팀 에이전트 간의 초기 간격 거리를 1로 설정한다.
#D 루프를 돌려 그리드의 왼쪽에 팀1을 배치한다.
#E 그리드 오른쪽에 팀2의 에이전트를 배치하기 위한 루프
#F 방금 위에서 만든 위치 List를 사용하여 팀1의 그리드에 에이전트를 추가한다.
먼저 이전 실험들과 마찬가지로 기본 매개 변수를 설정했다. 컴퓨팅 비용을 낮게 유지하기 위해 각 팀당 16개의 에이전트가 있는 30x30 그리드를 만들고 있지만 GPU가 있는 경우 더 많은 에이전트로 그리드를 더 크게 만들 수 있다. 각 팀마다 하나씩 총 두개의 매개 변수 벡터를 초기화한다. 이 실험에서도 DQN으로 간단한 2계층 신경망을 사용한다. 이제 그리드를 시각화 할 수 있다.
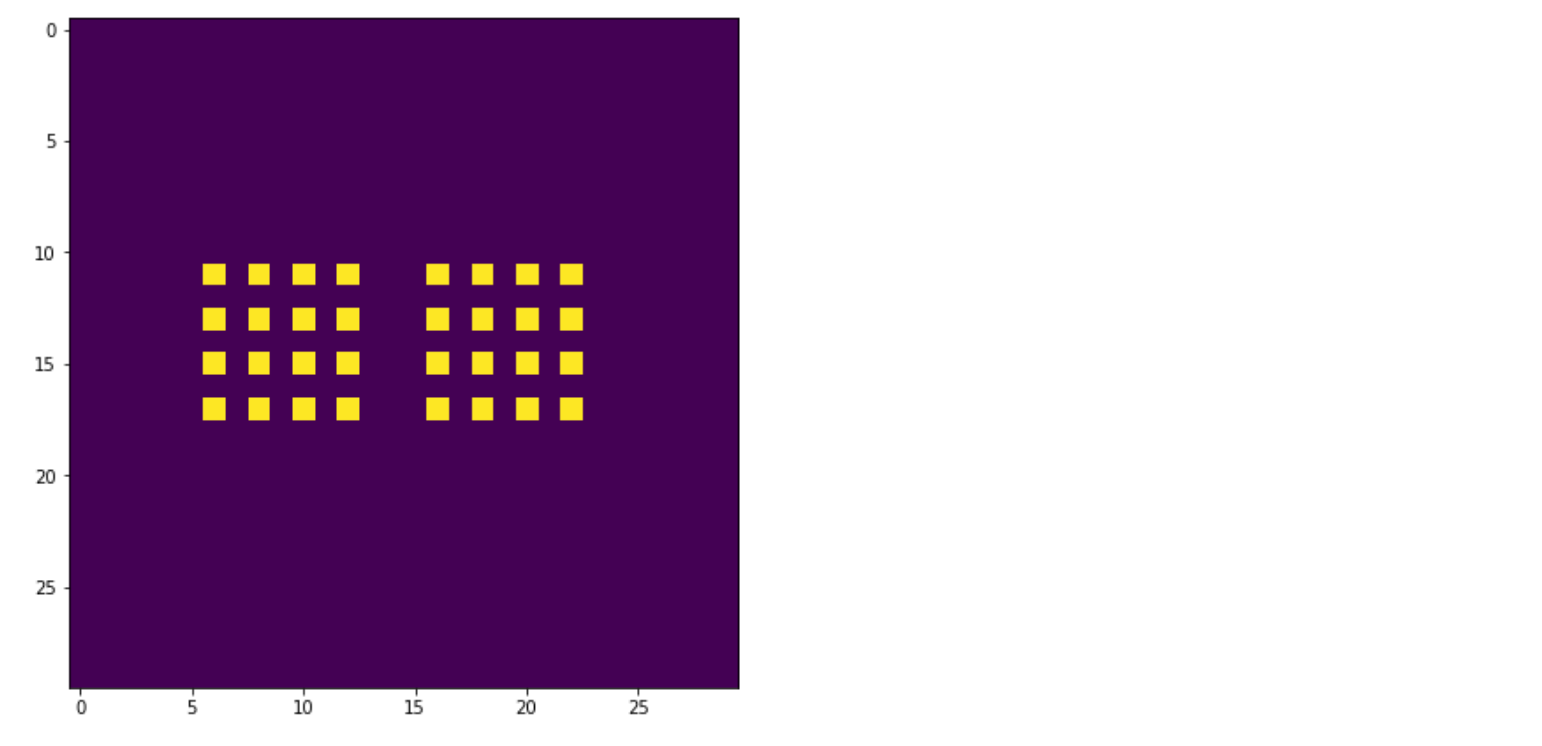
Figure 9.25 MAgent 환경에서 두 팀의 에이전트 시작 위치. 밝은 사각형은 개별 에이전트이다.
팀2는 왼쪽에 팀1은 오른쪽에 있다. 모든 에이전트는 사각형 패턴으로 초기화되며 팀은 하나의 그리드 사각형으로 구분된다. 각 에이전트의 Action space는 다음과 같이 길이가 21인 벡터이다.
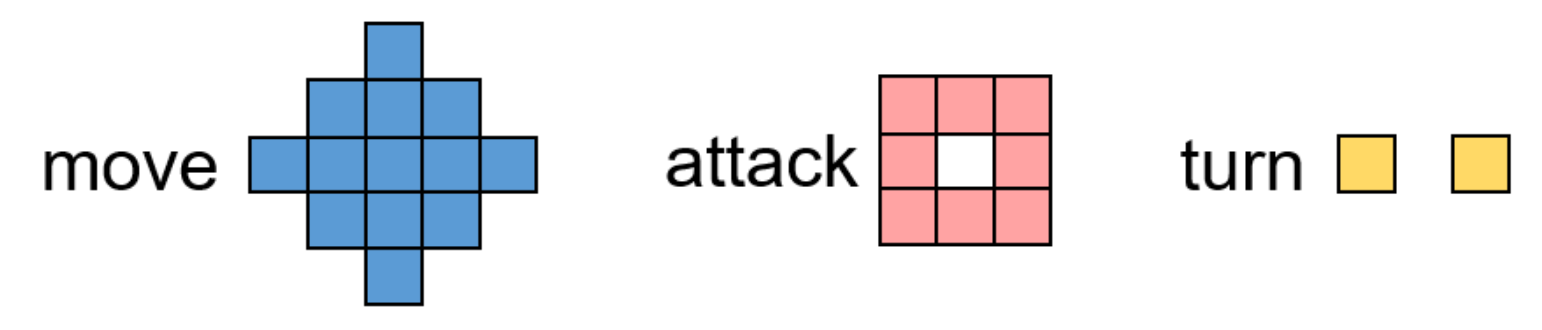
그림 9.26 MAgent 라이브러리에 있는 에이전트의 Action space를 보여준다. 각 에이전트는 13개의 다른 방향으로 이동하거나 8개의 방향으로 공격 할 수 있다. 회전 동작은 기본적으로 비활성화되어 있어서 Action space은 13 + 8 = 21이다.
Listing 9.15 이웃 찾기
def get_neighbors(j,pos_list,r=6): #A
neighbors = []
pos_j = pos_list[j]
for i,pos in enumerate(pos_list):
if i == j:
continue
dist = cityblock(pos,pos_j)
if dist < r:
neighbors.append(i)
return neighbors
#A`pos_list`에 있는 모든 에이전트의 [x, y] 위치가 주어지면 에이전트 j의 반경 내에 있는 에이전트의 인덱스를 반환한다.
각 에이전트의 FOV에서 이웃을 찾으려면 이 함수가 필요하다. env.get_pos(team1)을 사용하여 팀1의 각 에이전트에 대한 좌표 목록을 가져온 다음 색인 j와 함께 get_neighbors 함수에 전달하여 에이전트 j 의 이웃을 찾을 수 있다.
>>> get_neighbors(5,env.get_pos(team1))
[0, 1, 2, 4, 6, 7, 8, 9, 10, 13]
따라서 에이전트 5는 13x13 FOV 안에 팀1에 10개의 다른 에이전트가 있다. 몇 가지 다른 Helper 함수를 만들어야 한다. 환경이 받아들이고 반환하는 Action은 0에서 20까지의 정수이므로 이를 one-hot action-vector로 변환하고 다시 정수 형식으로 변환 할 수 있어야 한다. 또한 에이전트 주변의 이웃에 대한 평균 필드 벡터를 얻는 함수도 필요하다.
Listing 9.16 평균 필드 Action 계산하기
def get_onehot(a,l=21): #A
x = torch.zeros(21)
x[a] = 1
return x
def get_scalar(v): #B
return torch.argmax(v)
def get_mean_field(j,pos_list,act_list,r=7,l=21): #C
neighbors = get_neighbors(j,pos_list,r=r) #D
mean_field = torch.zeros(l)
for k in neighbors:
act_ = act_list[k]
act = get_onehot(act_)
mean_field += act
tot = mean_field.sum()
mean_field = mean_field / tot if tot > 0 else mean_field #E
return mean_field
#A 정수 표현을 one-hot 벡터 표현으로 변환
#B one-hot vector Action을 정수 표현으로 변환
#C 에이전트`j`의 평균 필드 Action을 가져 온다.`pos_list`는`env.get_pos (team1)`에 의해 리턴되며 `l`은 Action space의 차원이다.
#D`pos_list`를 사용하여 에이전트의 모든 이웃을 찾는다.
#E 0으로 나누지 않아야 한다.
get_mean_field 함수는get_neighbors 함수를 사용하여 에이전트j에 대한 모든 에이전트의 좌표를 가져온 다음 해당 Action 벡터를 가져 와서 더하고 합계로 나눈다. get_mean_field 함수는 대응하는 Action 벡터act_list (정수 기반 Action의 List)를 입력을 받는다. 여기서pos_list와act_list의 색인은 같은 에이전트를 가리킨다.
매개 변수r은 이웃으로 포함하고자 하는 에이전트j 주위의 그리드 사각형의 반경을 나타내며 l은 21인 Action space의 크기를 나타낸다.
Ising 모델 예제와는 달리, 각 에이전트에 대한 Action을 선택하기 위해 별도의 함수를 만들겠다. 학습하기에 더 복잡한 환경이기 때문에 조금 더 모듈화하려고 한다. 환경에서 각 Step이 진행됨에 따라, 모든 에이전트에 대한 관찰(Observation) 텐서를 동시에 얻는다.
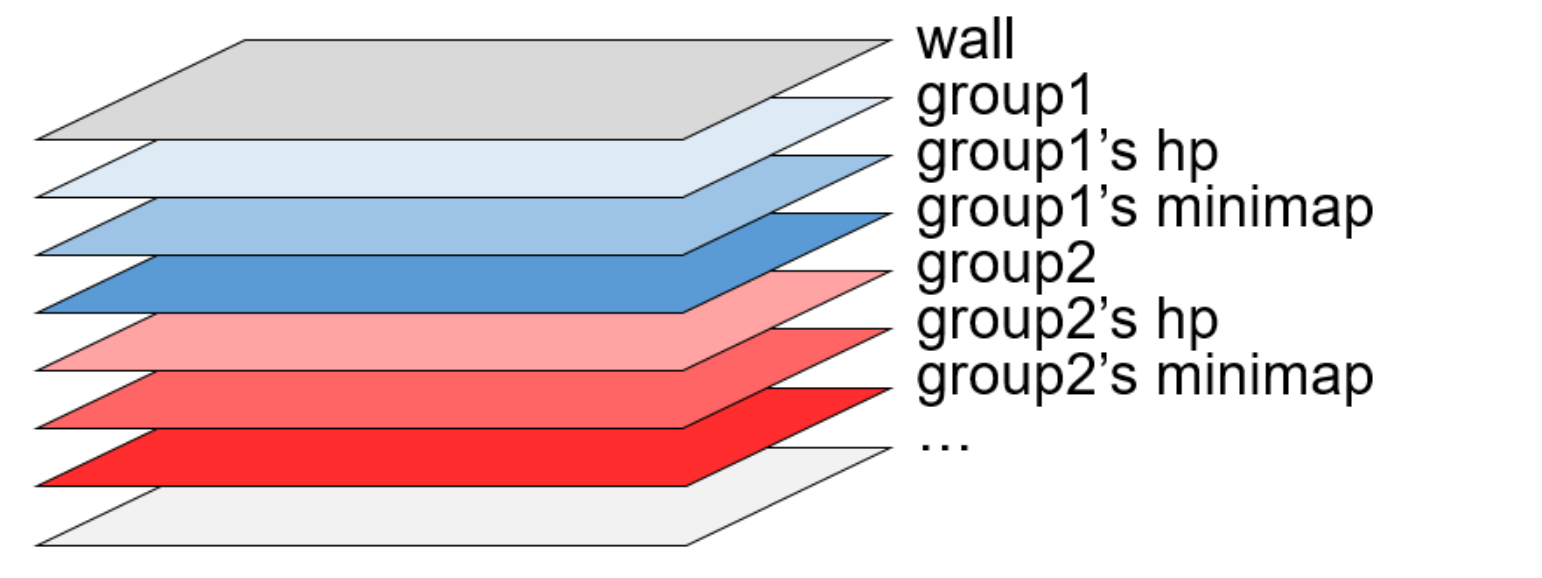
Figure 9.26 관측(Observation) 텐서의 구조를 보여준다. N × 13 × 13 × 7 텐서이며 여기서 N은 팀의 에이전트 수이다.
env.get_observation(team1)에 의해 반환된 관측 값은 실제로 두 개의 텐서가 있는 튜플이다. 첫 번째 텐서는 위 그림의 상단 부분에 표시되어 있다. 복잡한 고차원 텐서인 반면 튜플의 두 번째 텐서는 앞으로 무시할 추가적인 정보를 가지고 있다. 관찰(Observation) 또는 상태(State)를 말할 때 첫 번째 텐서를 의미한다.
관측 값은 N × 13 × 13 × 7 텐서이며 여기서 N은 에이전트 수이다(이 실험에서는 에이전트의 수가 16개임). 단일 에이전트에 대한 텐서의 각 13 × 13 슬라이스는 벽의 위치와 함께 FOV를 보여준다 (슬라이스 0) , 팀1 에이전트(슬라이스 1), 팀1 에이전트의 HP(슬라이스 2) 등. FOV 내에서 팀1과 팀2의 에이전트 위치인 슬라이스 1과 4만 사용한다. 따라서 단일 에이전트의 경우 관측 텐서가 13 × 13 × 2가 되고 벡터로 평면화하여 338 길이 State 벡터를 얻는다. 그런 다음이 State 벡터를 길이 21인 평균 필드 벡터와 연결(Concatenation)하여 Q-function에 넘기게 되는 338 + 21 = 359 길이의 벡터를 얻는다. Curiosity-based 학습에서와 같이 Two-headed 신경망을 사용하는 것이 이상적이다. 이렇게 하면 한 Head가 State 벡터를 처리 할 수 있고 다른 Head는 평균 필드 Action 벡터를 처리한 다음 처리된 정보를 이후 계층에 재결합(Recombine) 할 수 있습니다. 여기서는 단순화하기 위해 하지 않았지만 시도해 보는 것이 좋다.
Listing 9.17 Action 선택하기
def infer_acts(obs,param,layers,pos_list,acts,act_space=21,num_iter=5,temp=0.5):
N = acts.shape[0] #A
mean_fields = torch.zeros(N,act_space)
acts_ = acts.clone() #B
qvals = torch.zeros(N,act_space)
for i in range(num_iter): #C
for j in range(N): #D
mean_fields[j] = get_mean_field(j,pos_list,acts_)
for j in range(N): #E
state = torch.cat((obs[j].flatten(),mean_fields[j]))
qs = qfunc(state.detach(),param,layers=layers)
qvals[j,:] = qs[:]
acts_[j] = softmax_policy(qs.detach(),temp=temp)
return acts_, mean_fields, qvals
def init_mean_field(N,act_space=21):
mean_fields = torch.abs(torch.rand(N,act_space))
for i in range(mean_fields.shape[0]):
mean_fields[i] = mean_fields[i] / mean_fields[i].sum()
return mean_fields
#A 에이전트 수 얻기
#B 위치 변경을 피하기 위해 Action 벡터 복제
#C Action에 수렴하기 위해 몇 번 반복
#D 에이전트를 반복하여 이웃 평균 필드 Action 벡터를 계산한다.
#E 평균 필드 Action 및 State를 사용하여 Q-value을 계산하고 softmax Policy를 사용하여 Action을 선택한다.
#F 평균 필드 벡터를 Random 초기화한다.
infer_acts 는 관찰 후 각 에이전트에 대한 모든 Action을 결정하는 데 사용할 함수이다. param및 layers로 매개 변수화된 평균 필드 Q-function을 사용하여 softmax Policy를 사용하는 모든 에이전트의 Action을 샘플링한다.
PARAMETERS FOR THE
INFER_ACTSFUNCTION
`obs` : 관측 텐서 N x 13 x 13 x 2 이다.
`mean_fields` : 각 에이전트에 대한 모든 평균 필드 Action를 포함하는 N x 21 텐서이다.
`pos_list` : `env.get_pos (...)`에 의해 반환 된 각 에이전트의 위치 List이다.
`acts` : 각 에이전트 (N,)의 정수로 표현된 Action으로 구성된 벡터이다.
`num_iter` : Action 샘플링 또는 Policy 업데이트를 하는 반복 횟수이다.
`temp`는 Exploration Rate을 제어하기 위한 softmax Policy 온도(temperature)이다.
이 함수는 아래 튜플을 반환한다.
acts_ : Policy에서 샘플링된 정수 Action의 (N,) 벡터
mean_fields_ : (N, 21) 각 에이전트의 평균 필드 벡터 텐서
qvals : 각 에이전트의 각 Action에 대한 Q-value의 (N, 21) 텐서
마지막으로 학습을 위한 함수가 필요하다. 이 함수에 매개 변수 벡터를 제공하고 Exploration Replay Buffer를 구현하고 Minibatch를 통해 SGD(Stochastic Gradient Descent)를 수행하도록 한다.
Listing 9.18 학습 함수
def train(batch_size,replay,param,layers,J=64,gamma=0.5,lr=0.001):
ids = np.random.randint(low=0,high=len(replay),size=batch_size) #A
exps = [replay[idx] for idx in ids] #B
losses = []
jobs = torch.stack([ex[0] for ex in exps]).detach() #C
jacts = torch.stack([ex[1] for ex in exps]).detach() #D
jrewards = torch.stack([ex[2] for ex in exps]).detach() #E
jmeans = torch.stack([ex[3] for ex in exps]).detach() #F
vs = torch.stack([ex[4] for ex in exps]).detach() #G
qs = []
for h in range(batch_size):#H
state = torch.cat((jobs[h].flatten(),jmeans[h]))
qs.append(qfunc(state.detach(),param,layers=layers)) #I
qvals = torch.stack(qs)
target = qvals.clone().detach()
target[:,jacts] = jrewards + gamma * torch.max(vs,dim=1)[0] #J #20 = 20 + 20
loss = torch.sum(torch.pow(qvals - target.detach(),2))
losses.append(loss.detach().item())
loss.backward()
#SGD
with torch.no_grad(): #K
param = param - lr * param.grad
param.requires_grad = True
return np.array(losses).mean()
#A Exploration Replay 를 Subset하기 위해 무작위 인덱스 List를 생성한다.
#B 미니 배치를 위해 Exploration Replay Buffer 를 Subset한다.
#C 미니 배치에서 단일 텐서로 모든 State 수집
#D 미니 배치에서 단일 텐서로 모든 Action 수집
#E 미니 배치에서 모든 Reward을 단일 텐서로 수집
#F 미니 배치에서 단일 텐서로 모든 평균 필드 Action 수집
#G 미니 배치에서 단일 텐서로 모든 State-value 수집
#H 미니 배치에서 각 경험을 반복한다.
#I Exploration Replay의 각 경험에 대한 Q-value 계산
#J Target Q-value 계산
#K 확률적 경사 하강(Stochastic Gradient Descent)
이 함수는 State 정보가 더 복잡하다는 점을 제외하고 2D Ising Model로 Exploration Replay하는 것과 거의 같은 방식으로 작동한다.
PARAMETERS FOR THE TRAIN FUNCTION
학습 함수는 Exploration Replay Buffer에 저장된 경험을 사용하여 단일 신경망을 학습시킨다.
Inputs:
`batch_size`, int
`replay`, list of tuples (obs 1 small, acts 1,rewards1,act means1,qnext1)
`param`, vector, neural network parameter vector
`layers`, list, contains shape of neural network layers,
`J`, int, number of agents on this team
`gamma`, float in [0,1], discount factor
`lr`, float, learning rate for SGD
Returns
`loss` (float)
이제 환경을 설정하고, 두 팀의 에이전트를 설정하고, 여러 가지 함수를 정의하여 궁극적으로 필드 Q-learning에 사용하는 두 개의 DQN을 학습시킬 수 있다. 이제 게임 플레이의 주요 부분에 들어간다. 코드가 많지만 대부분은 자주 사용되는 코딩 패턴이며 전체 알고리즘을 이해하는 데 그리 중요하지 않다. 먼저 Exploration Replay Buffer와 같은 예비 데이터 구조를 설정하겠다. 팀1과 팀2에 대해 별도의 Exploration Replay Buffer가 필요하다. 실제로, 팀1과 팀2에 대해 거의 모든 것을 분리해서 코딩하는 것이 필요하다.
Listing 9.19 Action 초기화하기
N1 = env.get_num(team1) #A
N2 = env.get_num(team2)
step_ct = 0
acts_1 = torch.randint(low=0,high=act_space,size=(N1,)) #B
acts_2 = torch.randint(low=0,high=act_space,size=(N2,))
replay1 = deque(maxlen=replay_size) #C
replay2 = deque(maxlen=replay_size)
qnext1 = torch.zeros(N1) #D
qnext2 = torch.zeros(N2)
act_means1 = init_mean_field(N1,act_space) #E
act_means2 = init_mean_field(N2,act_space)
rewards1 = torch.zeros(N1) #F
rewards2 = torch.zeros(N2)
losses1 = []
losses2 = []
#A 각 팀의 에이전트 수를 저장한다.
#B 모든 에이전트에 대한 Action을 초기화한다.
#C Exploration Replay Buffer 사용을 위해 deque 데이터 구조를 생성한다.
#D Q(s') value를 저장할 텐서를 생성한다.
#E 각 에이전트의 평균 필드를 초기화한다.
#F 각 에이전트에 대한 Reward를 저장할 텐서를 생성한다.
각 에이전트에 대한 Action(정수), 평균 필드 Action 벡터, Reward 및 다음 State Q-value를 추적하여 이를 경험으로 패키지하고 Exploration Replay 시스템에 추가한다.
Listing 9.20 팀 단계를 수행하기 함수와 Replay Buffer에 추가하기 함수
def team_step(team,param,acts,layers):
obs = env.get_observation(team) #A
ids = env.get_agent_id(team) #B
obs_small = torch.from_numpy(obs[0][:,:,:,[1,4]]) #C
agent_pos = env.get_pos(team) #D
acts, act_means, qvals = infer_acts(obs_small,\
param,layers,agent_pos,acts) #E
return acts, act_means, qvals, obs_small, ids
def add_to_replay(replay,obs_small, acts,rewards,act_means,qnext): #F
for j in range(rewards.shape[0]): #G
exp = (obs_small[j], acts[j],rewards[j],act_means[j],qnext[j])
replay.append(exp)
return replay
#A 16x13x13x7 텐서인 팀1에서 관측(Observation) 텐서를 가져온다.
#B 아직 살아있는 에이전트의 인덱스 목록을 가져온다.
#C 에이전트의 위치를 얻기 위해 관측 텐서를 Subset한다.
#D 팀1의 각 에이전트에 대한 좌표 List를 가져온다.
#E 각 에이전트에 대해 DQN을 사용하여 수행할 Action을 결정한다.
#F 각 개별 에이전트의 경험을 Replay Buffer에 별도로 추가한다.
#G 각 에이전트에 대해서 루프를 돈다.
team_step함수는 메인 루프의 주요 코딩 영역이다. 이를 통해 환경에서 모든 데이터를 수집하고 DQN을 실행하여 수행할 Action을 결정한다. add_to_replay 함수는 관측 텐서, Action 텐서, Reward 텐서, Action 평균 필드 텐서 및 다음 State Q-value 텐서를 가져 와서 각 개별 에이전트 경험을 Replay Buffer에 별도로 추가한다. 나머지 코드는 모두 while 루프 내에 있으므로 코드를 여러 부분으로 나눌 것이지만 모두 동일한 루프의 일부임을 기억하자. 또한 이 책의 GitHub (https://github.com/DeepReinforcementLearning/DeepReinforcementLearningInAction/) 에 있는 Jupyter Notebooks에 이 코드가 모두 포함되어 있으며 시각화 및 기타 주석을 작성하는 데 사용하는 모든 코드가 포함되어 있다.
Listing 9.21 학습 루프
for i in range(epochs):
done = False
while not done: #A
acts_1, act_means1, qvals1, obs_small_1, ids_1 = \
team_step(team1,params[0],acts_1,layers) #B
env.set_action(team1, acts_1.detach().numpy().astype(np.int32)) #C
acts_2, act_means2, qvals2, obs_small_2, ids_2 = \
team_step(team2,params[0],acts_2,layers)
env.set_action(team2, acts_2.detach().numpy().astype(np.int32))
done = env.step() #D
_, _, qnext1, _, ids_1 = team_step(team1,params[0],acts_1,layers) #E
_, _, qnext2, _, ids_2 = team_step(team2,params[0],acts_2,layers)
env.render() #F
rewards1 = torch.from_numpy(env.get_reward(team1)).float() #G
rewards2 = torch.from_numpy(env.get_reward(team2)).float()
#A 게임이 끝나지 않은 동안
#B`team_step` 메소드를 사용하여 환경 데이터를 수집하고 DQN을 사용하여 에이전트에 대한 Action을 선택한다.
#C 환경에서 선택한 Action을 인스턴스화한다.
#D 새로운 관측과 Reward를 생성할 환경에서 한 Step 나간다.
#E 환경에서 다음 State에 대한 Q-value을 얻기 위해 `team_step`을 다시 실행한다.
#F 환경을 렌더링한다.
#G 각 에이전트에 대한 Reward를 텐서로 수집한다.
while 루프는 게임이 끝나지 않는 한 계혹 실행되고 한 팀의 모든 에이전트가 죽을 때 게임이 끝난다. team_step함수 내에서 먼저 관측 텐서를 가져오고 앞에서 설명한대로 원하는 부분을 Subset하여 13x13x2 텐서를 생성한다. 또한 팀1에 아직 살아있는 에이전트의 인덱스인 ids_1도 얻는다. 또한 각 팀에서 각 에이전트의 좌표 위치를 가져와야 한다. 그런 다음infer_acts 함수를 사용하여 각 에이전트에 대한 Action을 선택하고 환경에서 이를 인스턴스화하고 마지막으로 새로운 관측 및 Reward를 생성하는 환경의 한 Step을 수행한다. while 루프를 계속해서 살펴보자.
Listing 9.21 학습 루프
replay1 = add_to_replay(replay1, obs_small_1, acts_1,rewards1,act_means1,qnext1) #A
replay2 = add_to_replay(replay2, obs_small_2, acts_2,rewards2,act_means2,qnext2)
shuffle(replay1) #B
shuffle(replay2)
ids_1_ = list(zip(np.arange(ids_1.shape[0]),ids_1)) #C
ids_2_ = list(zip(np.arange(ids_2.shape[0]),ids_2))
env.clear_dead() #D
ids_1 = env.get_agent_id(team1) #E
ids_2 = env.get_agent_id(team2)
ids_1_ = [i for (i,j) in ids_1_ if j in ids_1] #F
ids_2_ = [i for (i,j) in ids_2_ if j in ids_2]
acts_1 = acts_1[ids_1_] #G
acts_2 = acts_2[ids_2_]
step_ct += 1
if step_ct > 250:
break
if len(replay1) > batch_size and len(replay2) > batch_size: #H
loss1 = train(batch_size,replay1,params[0],layers=layers,J=N1)
loss2 = train(batch_size,replay2,params[1],layers=layers,J=N1)
losses1.append(loss1)
losses2.append(loss2)
#A Experience Replay에 추가한다.
#B Replay Buffer를 셔플링한다.
#C 어느 에이전트가 죽었고 그리드에서 사라질지를 추적하기 위해 Zip된 ID List를 작성한다.
#D 그리드에서 죽은 에이전트를 지운다.
#E 이제 죽은 에이전트가 지워졌으므로 새 에이전트 ID List를 가져온다.
#F 아직 존재하는 에이전트를 기반으로 이전 ID List를 Subset한다.
#G 아직 존재하는 에이전트를 기반으로 Action List를 Subset한다.
#H Replay Buffer가 차면 학습을 시작한다.
이 코드의 마지막 부분은 튜플에 모든 데이터를 수집하고 학습을 위해 Experience Replay Buffer에 추가하는 것이다. MAgent의 한 가지 복잡한 점은 에이전트가 죽으면 시간이 지남에 따라 에이전트 수가 감소한다는 점이다. 따라서 시간이 지남에 따라 데이터를 올바른 에이전트와 일치 시키려면 Array를 잘 다루어야 한다.
작은 Epoch 에서 조차도 학습 루프를 실행했을 때, 그리드가 자고 각 팀에 16개의 에이전트만 있기 때문에 에이전트가 바로 전투 기술을 보여주기 시작한다. https://github.com/geek-ai/MAgent/blob/master/doc/get_started.md 지침에 따라 녹화된 게임의 비디오를 보자.
에이전트들이 서로 공격을 시작하고 동영상이 끝나기 전에 에이전트들이 죽는 것도 볼 수 있다. 다음은 동영상 끝부분의 스크린 샷이다.

Figure 9.27 Mean Field Q-learning을 이용한 학습 후 MAgent 전투 게임의 스크린 샷. 파란 팀이 빨간 팀을 모퉁이에 밀어 붙여 공격하고 있다.
9.6 Summary
- 멀티 에이전트 설정에서 일반 Q-learing이 제대로 작동하지 않는다. 이는 모든 에이전트가 새로운 Policy를 배우고 있어 환경이 Non-stationary 지기 때문이다.
- 환경의 불안정성(Non-stationarity)은 Reward의 Expected Value가 시간이 지남에 따라 변한다는 것을 의미한다.
- 불안정성(Non-stationarity)을 처리하기 위해 Q-function은 다른 에이전트의 Joint Action space에 액세스 할 수 있어야 하지만 이 Joint Action space은 에이전트 수의 지수적 확장으로 인해 대부분의 실제 문제에 적용할 때 다루기가 어려워 진다.
- 이웃 Q-learning은 주어진 에이전트의 인접 이웃의 Joint Action space에 대해서만 계산하여 지수 스케일링을 완화할 수 있지만, 이웃 수가 많으면 이것도 다루기에 너무 큰 스케일이 된다.
- MF-Q(Mean Field Q-learning)는 전체 Joint Action space이 아닌 평균 Action만 계산하므로 에이전트 수에 따라 지수적이 아닌 선형적으로 확장된다.

Leave a comment