DRL Evolutionary Strategies

Chapter 6. Alternative Optimization Methods - Evolutionary Strategies

(Alternative 최적화 방법: Evolutionary Strategies 진화 전략)

(Orinial Book = ‘Deep Reinforcement Learning in Action’ by Alexander Zai and Brandon Brown)

이 장에서 다룰 내용 :

• 진화 전략(Evolutionary Strategies) 최적화 기법 이란?
• 진화 전략(Evolutionary Strategies) 최적화 기법 vs 기존 최적화 알고리즘 의 장단점
• 역전파(Backpropagation) 을 사용하지 않고 CartPole game 구현
• 진화 전략(Evolutionary Strategies) 최적화 기법이 기존 최적화 알고리즘에 비해 보다 확장가능한 이유

6.1 강화 학습(Reinforcement Learning) 의 다른 접근 방식

다음 알고리즘은 이전에 사용한 접근 방식과 약간 다르다. DQN 및 Policy Gradient(PG) 알고리즘의 경우 Q-function 또는 Policy function을 근사하기 위해 신경망에 의존하는 에이전트를 만들어야 했다. 에이전트는 환경과 상호 작용하고 경험을 수집한 다음 역전파를 사용하여 신경망의 정확성을 향상 시킨다. 올바른 optimizer function 선택, 초기 학습 속도(learning rate) 선택, 학습 속도 스케쥴(learning rate schedule) 선택, 에이전트가 합리적인 시간 내에 학습 할 수 있도록 미니 배치 크기(minibatch size) 필요한 경우 Replay Buffer 까지 다양한 하이퍼파라미터(hyperparameter)를 신중하게 조정해야 했다. DQN 및 PG 알고리즘은 이름에서 알 수 있듯이 Noise Gradient에 의존하는 Stochastic Grdient Descent 에 의존하기 때문에 이러한 모델이 성공적으로 학습 될 것이라는 보장이 없다 (즉, Local Optima 또는 Global Optima에 수렴).

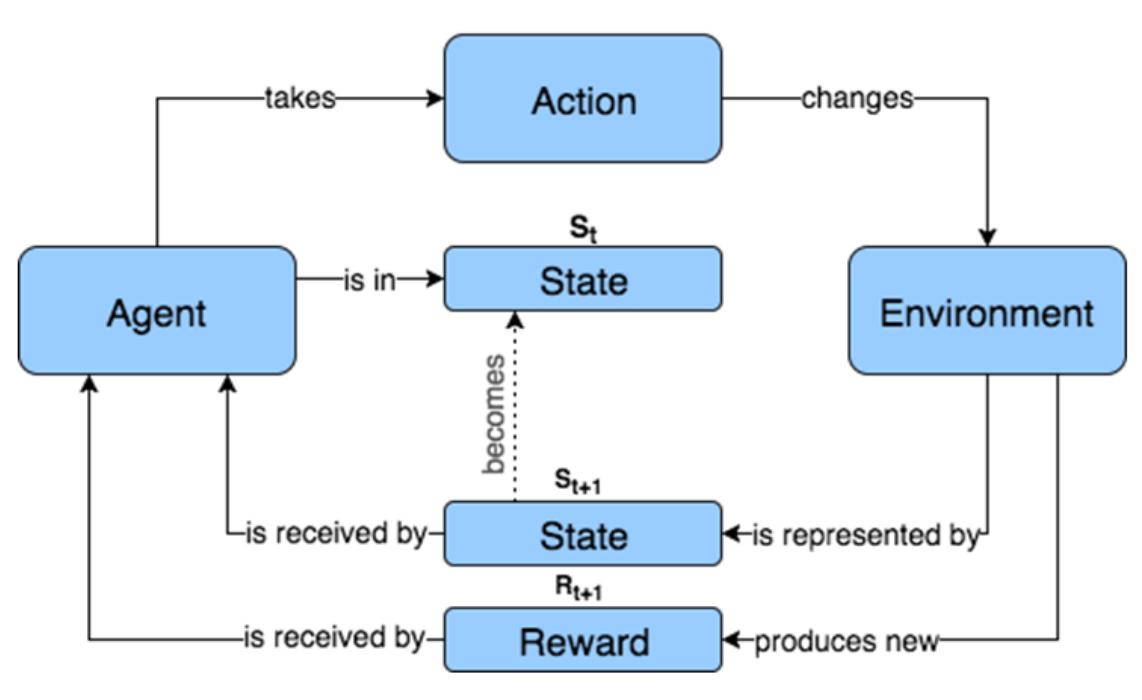
Figure 6.1: 우리가 다루었던 과거 알고리즘의 경우 에이전트는 환경과 상호 작용하고 경험을 수집한 다음 해당 경험에서 배웠다. 에이전트가 학습을 중단 할 때까지 각 Epoch에 대해 동일한 프로세스를 반복하고 반복했다.

신경망의 복잡성과 환경에 따라 적절한 하이퍼파라미터를 사용하여 에이전트를 만들어 내는 것은 매우 어려울 수 있다. 또한 경사 하강법(Gradient Descent) 및 역전파(Backpropagation)를 사용하려면 미분 가능한(differentiable) 모델이 필요하다. 흥미롭고 유용한 모델일지 모르지만, 미분 불가능한 경우와 같이 경사 하강법으로 학습 할 수 없는 모델을 새로운 방식으로 만들 수 있다. 하나의 에이전트를 만들고 개선하는 방식 대신 Charles Darwin의 자연 선택에 의한 진화론을 이용하면 어떨까? 다른 매개 변수(Weight)로 여러 개의 다른 에이전트들을 만들고 그 중에서 가장 좋은 에이전트가 무엇인지 관찰하고 진화론의 자연 선택과 마찬가지로 자손들이 부모의 특성을 상속받을 수 있도록 최고의 에이전트를 키워 낼 수 있다. 알고리즘을 사용하여 생물학적 에뮬레이션을 할 수 있다. 하이퍼파라미터를 조정하고 에이전트가 정확하게 학습하고 있는지 확인하기 위해 여러 Epoch를 기다릴 필요가 없다. 생물학적 에뮬레이션을 통해 훨씬 더 나은 결과를 내는 에이전트를 선택할 것이다.

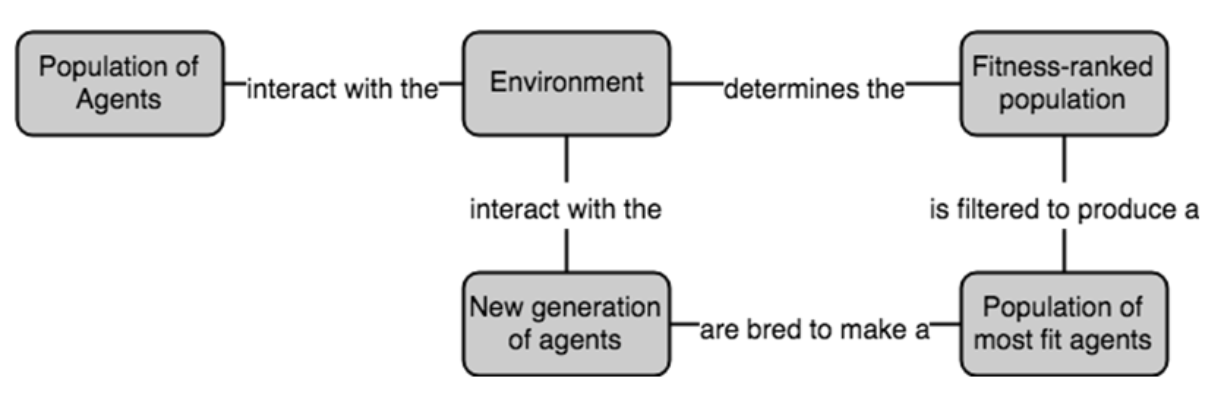
Figure 6.2: 진화 알고리즘은 경사 하강법 기반 최적화 기법과 다르다. 진화 전략을 통해 에이전트를 생성하고 가장 유리한 가중치(weight)를 자손 에이전트로 전달한다.

이 알고리즘은 개별 에이전트가 학습할 필요가 없으며 Gradient Descent에 의존하지 않으며 Gradient-Free 알고리즘 이라고도 한다. 그러나 개별 에이전트가 어떤 목표를 향해 직접 유도되고 있지 않다고 해서 반드시 우연한 기회에 의존한다는 의미는 아니다. 저명한 진화 생물 학자 Richard Dawkins 은 “자연 선택은 무작위 일뿐(Natural selection is anything but random.)”이라고 말했다. 이 말은, 최고의 에이전트를 만들거나 보다 정확하게 발견하려는 노력에 있어서 순전히 우연한 기회에 의존하는 것이 아니라 특성에 차이가 있는 모집단 중에서 가장 적합한 것을 선택하는 것에 의존한다.

6.2 진화 전략(Evolutionary Strategies) 을 이용한 강화학습

이 섹션에서는 Fitness가 진화 전략에 미치는 영향에 대해 설명하고 가장 적합한 에이전트를 선택하는 작업에 대해 간략하게 설명한다. 다음으로 이러한 에이전트를 새로운 에이전트로 재결합하는 방법과 돌연변이를 도입 할 때 어떤 일이 발생하는지 보여줄 것이다. 이 진화는 다세대 프로세스(multiple-generation process)이므로 이에 대해 논의하고 전체 학습 과정을 다시 살펴 보겠다.

6.2.1 적합성(Fitness)

고등학교 생물학 수업을 기억한다면, 자연 선택은 각 세대의“가장 적합한” 개체를 선택한다. 생물학에서 이것은 가장 번식적인 성공을 거둔 개체를 나타내며, 따라서 그들의 유전 정보를 다음 세대에 전달했다. 나무에서 씨앗을 구할 때 부리 모양을 가진 새는 더 많은 씨앗을 먹을 수 있으므로 부리 모양 유전자를 자녀와 손자에게 전달시킬 수 있다. 그러나 “가장 적합하다” 라는 것은 환경과 관련이 있다. 북극곰은 북극 얼음 지역에 잘 맞지만 아마존 열대 우림에는 적합하지 않다. 환경을 개체가 해당 환경 내에서 수행 한 성과에 따라 적합성 점수를 부여하는 목적 함수 또는 적합성 함수를 결정하는 것으로 생각할 수 있으며, 그 성과는 전적으로 유전 정보에 의해 결정된다.

진화론적 강화 학습에서 우리는 에이전트에게 주어진 환경에서 최고의 보상을 주는 특성을 선택하고 특성에 의해 모델의 매개 변수(예 : 신경망의 가중치) 또는 전체 모델 구조가 의미있게 된다. RL 에이전트의 정합성은 환경에서 수행 할 경우 받을 것으로 예상되는 보상에 따라 결정될 수 있다. A 에이전트가 Atari 게임을 했다고 가정하자. A 에이전트가 Breakout 게임에서 평균 500 점을 달성 할 수 있지만 B 에이전트는 300 점만 얻을 수 있다고 가정하면, 에이전트 A가 에이전트 B보다 덕 적합하고 최적의 에이전트가 B보다 A와 더 유사하게 된다. 그리고 에이전트 A가 에이전트 B보다 더 적합한 이유는 모델 매개 변수 때문이다. 환경에 약간 더 최적화되어 있다.

진화 강화 학습의 목표는 과거에 익숙했던 개념과 정확히 동일하다. 유일한 차이점은 신경망과 같은 모델의 매개 변수를 최적화하기 위해 종종 유전자 알고리즘이라고 불리는 진화적 과정을 사용한다는 것이다. 과정은 매우 간단하지만 유전자 알고리즘의 단계를 보다 자세히 살펴 보겠다. 설명은 일반인 내용이지만 나중에 이 내용이 강화 학습 문제에 적용된다.

신경망 모델이나 다른 기계 학습 모델 일 수 있는 함수 f(x, params)가 있고, 입력 x와 벡터 params를 취하는 매개 변수 집합을 찾으려고 한다. 주어진 함수의 출력은 최대값 또는 최소값을 취한다. 신경망의 비용 함수(Cost Function) 인 경우 입력에 따른 비용을 최소화하는 매개 변수 집합을 찾고자 한다. Gradient Descent를 사용하여 매개 변수와 관련하여 함수의 그래디언트를 계산하고 해당 그래디언트 정보를 사용하여 함수의 최소값을 향한 작고 확률적인 단계를 수행한다(Stochastic Gradient Descent). 이 같은 문제가 유전자 알고리즘으로 어떻게 해결되는지 보자.

• 랜덤 포텐셜 솔루션(Random Potential Solution)의 초기 모집단 (즉, 모수 벡터를 가진 모집단)을 생성한다. 모집단의 각 모수 벡터를 개체(individual)이라고 한다. 이 초기 모집단이 100개의 개체를 가진다고 가정 해 봅자.
• 그런 다음이 반복해서 모집단의 해당 매개 변수 세트로 모델을 실행하고 모델 출력을 기록하여 각 개체의 적합성을 평가한다. 각 개체에게는 훈련 데이터에 대한 성과를 기준으로 적합성 점수가 할당된다.

• 우리는 “교배 모집단(breeding population)”을 만들기 위해 상대적 적합성 점수(적합성이 높은 개체가 선택 될 확률이 높음)에 따라 가중치를 둔 모집단에서 무작위로 한 쌍의 개체(“부모”)을 샘플링한다.

  NOTE: 다음 세대를 위한 “부모”를 선택하는 방법에는 여러 가지가 있다. 한 가지 방법은 상대적인 적합성 점수를 기반으로 각 개인에게 선택 확률을 간단히 매핑한 다음 이 분포에서 표본을 추출하는 것이다. 이러한 방식에서는 가장 적합한 것이 가장 많이 선택되지만, 불충분한 성과를 낼 가능성은 여전히 적다. 이것은 모집단의 다양성을 유지하는 데 도움이 될 수 있다. 또 다른 방법은 모든 개인의 순위를 정하고 정렬하고 상위 N 명의 개체을 데리고 다음 세대를 채우기 위해 짝짓기를 하는 것이다. 짝을 짓기 위해 최고의 성과를 가진 개체를 우선적으로 선택하는 것은 거의 모든 경우에 있어 효과가 있다.

• 이 교배 모집단의 개체는 100 명의 새 모집단을 만드는 “자손”을 생산하기 위해 “교배”할 것이다. 예를 들어, 개체가 단순히 실수의 벡터 (예 : 매개 변수 벡터) 인 경우 벡터 1과 벡터 2을 짝 짓는 것은 벡터 1에서 부분 집합을 가져와 이를 벡터 2의 상보 부분 집합(complementary subset)과 결합하여 만든다. 예를 들어, 벡터 1 : [1 2 3], 벡터 2 : [4 5 6]. 벡터 1은 벡터 2와 짝을 이루어 [1 5 6] 및 [4 2 3]을 생성한다. 단순히 교배 모집단의 개체를 무작위로 짝을 짓고 재결합하여 새 모집단을 채울 때까지 2 개의 새로운 자손을 생산한다.
• 이제 새로운 자손을 반복적으로 만들어 마지막 세대까지 새롭게 된 모집단를 확보했다. 이 시점에서 우리는 작업을 반복하고 일부를 무작위로 변경하여 모든 세대에 새로운 “유전자 다양성”을 도입 할 것이고 이것이 지역 최적(local optimum)의 조기 수렴을 방지한다. 돌연변이는 단순히 매개 변수 벡터에 약간의 랜덤 노이즈를 추가하는 것을 의미한다. 이것이 이진 벡터라면, 돌연변이는 무작위로 비트를 뒤집는 것이다. 중요한 것은 돌연변이율이 상당히 낮아야한다는 것이다. 그렇지 않으면 이미 존재하는 좋은 방법을 망칠 위험이 있다.
• N 세대 동안 또는 수렴에 도달 할 때까지 이 프로세스를 반복한다 (이 경우, 모집단의 평균 적합성은 크게 향상되지 않음).

진화론적 강화 학습 응용 프로그램에 들어가기 전에 간단한 예로 매우 간단한 유전자 알고리즘을 실행한다. 우리는 무작위 문자열의 집단을 만들고“Hello World!”와 같이 선택한 목표 문자열로 진화시키려고 할 것이다. 따라서 “gMIgSkybXZyP”및 “adlBOM XIrBH”와 같은 임의의 문자열로 시작한 다음이 문자열이 대상 문자열 “Hello World!”와 얼마나 유사한 지 알려주는 함수를 사용한다. 적합성 점수를 제공하는데 “Hello World!”와 더 유사한 문자열 다음 세대에 선택 될 가능성이 더 높다.

모집단의 모든 초기 무작위 문자열에 점수를 매긴 다음 상대적 적합성 점수에 따라 가중치가 부여된 모집단에서 부모 쌍을 샘플링하게 되고 이로써 더 높은 적합성 점수를 가진 개체가 부모가 될 가능성이 높아 진다. 그런 다음 이 부모를 “결합”(교차 또는 재조합이라고도 함)하여 두 자손을 만들어 다음 세대에 추가한다. 또한 문자열에서 몇 문자를 무작위로 뒤집어 자손을 변경한다. 이 과정를 반복하고 결국 모집단이 목표에 매우 가까운 문자열로 수렴해질 것으로 예상하고 적어도 하나는 목표에 정확히 도달 할 것이다 (이 시점에서 알고리즘을 중지하게 된다). 물론이 특정 사례가 실제로 어떻게 유용할 지는 생각할 수 없지만 유전자 알고리즘의 가장 간단한 예 중 하나이며 이 개념은 강화 학습 테스크에 직접 적용되기도 한다.

Listing 6.1 진화하는 문자열

import random
from matplotlib import pyplot as plt

alphabet = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ,.! " #A
target = "Hello World!" #B

class Individual: #C
	def __init__(self, string, fitness=0):
		self.string = string
		self.fitness = fitness

from difflib import SequenceMatcher

def similar(a, b): #D
	return SequenceMatcher(None, a, b).ratio()

def spawn_population(length=26,size=100): #E
	pop = []
	for i in range(size):
		string = ''.join(random.choices(alphabet,k=length))
		individual = Individual(string)
		pop.append(individual)
	return pop

#A 임의의 문자열(random strings)을 생성하기 위해 샘플링한 문자 목록(List of characters)이다.

#B 무작위 모집단으로 부터 진화하려는 문자열(string)이다.

#C 모집단의 각 원소에 대한 정보를 저장하는 간단한 Class를 설정한다.

#D 두 문자열 사이의 유사성 메트릭을 계산하여 적합성 점수를 리턴하는 함수.

#E 문자열의 초기 무작위 모집단을 생성한다

지금까지 코드는 문자열 필드와 적합성 점수 필드로 구성된 클래스 객체인 개체(Individual)의 초기 모집단을 만들었다. 알파벳 문자 목록에서 샘플링하여 임의의 문자열을 만든다. 모집단을 확보 한 후 각 개체의 적합성을 평가해야한다. 뒤에 보게될 것과 같이, 유사성 메트릭은 기계 학습 모델을 사용할 때 손실 함수가 될 것이지만, 문자열의 경우 내장 Python 함수를 사용하여 유사성 메트릭을 계산할 수 있다.

Listing 6.1 진화하는 문자열(계속)

def recombine(p1_, p2_): #F
	p1 = p1_.string
	p2 = p2_.string
	child1 = []
	child2 = []
	cross_pt = random.randint(0,len(p1))
	child1.extend(p1[0:cross_pt])
	child1.extend(p2[cross_pt:])
	child2.extend(p2[0:cross_pt])
	child2.extend(p1[cross_pt:])
	c1 = Individual(''.join(child1))
	c2 = Individual(''.join(child2))
	return c1, c2

def mutate(x, mut_rate=0.01): #G
	new_x_ = []
	for char in x.string:
		if random.random() < mut_rate:
			new_x_.extend(random.choices(alphabet,k=1))
		else:
			new_x_.append(char)
	new_x = Individual(''.join(new_x_))
	return new_x

#F 이 함수는 두 개의 부모 문자열을 두 개의 새로운 자손으로 재조합한다. #G 이 함수는 무작위로 문자를 뒤집어 문자열을 변경한다.

재조합 함수는 단순히 “hello there”와 “fog world”와 같은 두 개의 부모 문자열을 가져 와서 문자열 길이까지 임의의 정수를 생성하고 부모 1의 첫 번째 조각과 부모 2의 두 번째 조각을 가져 와서 임의로 재조합한다. 분할이 중간에 발생한 경우 “fog there”및 “hello world”와 같은 자손을 만든다. 즉, “hello”와 같이 원하는 부분이 포함된 문자열과 “world”와 같은 원하는 부분이 포함된 다른 문자열로 진화시킨 경우와 같이 재조합 프로세스를 통해 원하는 결과를 얻을 수 있다.

돌연변이 프로세스(mutation process)은 “hellb”와 같은 문자열을 취하며 약간의 확률(돌연변이 비율, mutation rate)로 문자열의 문자를 임의의 문자로 대체한다. 예를 들어, 돌연변이 비율(mutation rate)이 20% (0.2) 인 경우 아마도 “hellb”의 5 개 문자 중 적어도 하나가 임의의 문자로 변이 될 것이다. 이것이 우리의 경우 “hello”로 변이되기를 바란다. 돌연변이의 목적은 모집단에 새로운 정보(변화량, variance)를 도입하는 것이다. 재결합만을 고려하고 돌연변이가 없다면, 개체군의 모든 개체가 너무 빨리 비슷해져서 각 세대마다 정보가 손실되기 때문에 원하는 해결책을 찾지 못할 것이다. 돌연변이 비율(mutation speed)은 매우 중요하다. 너무 높으면 가장 적합한 개인이 돌연변이로 적합성을 잃을 것이고 너무 낮으면 최적의 개체를 찾기에 충분한 변화량(variance)이 없다. 불행하게도, 우리는 경험적으로 적당한 돌연변이 비율를 찾아야 한다.

Listing 6.1 진화하는 문자열(계속)

def evaluate_population(pop, target): #H
	avg_fit = 0
	for i in range(len(pop)):
		fit = similar(pop[i].string, target)
		pop[i].fitness = fit
		avg_fit += fit
	avg_fit /= len(pop)
	return pop, avg_fit

def next_generation(pop, size=100, length=26, mut_rate=0.01): #I
	new_pop = []
  while len(new_pop) < size:
		parents = random.choices(pop,k=2, weights=[x.fitness for x in pop])
		offspring_ = recombine(parents[0],parents[1])
		child1 = mutate(offspring_[0], mut_rate=mut_rate)
		child2 = mutate(offspring_[1], mut_rate=mut_rate)
		offspring = [child1, child2]
		new_pop.extend(offspring)
	return new_pop

#H 이 함수는 모집단의 각 개체에게 적합성 점수를 할당한다. #I 이 함수는 재조합(recombine)과 돌연변이(mutate) 함수를 이용해 새로운 세대를 생성한다.

진화 과정을 완료하는 데 필요한 마지막 두 가지 함수를 보자. 하나는 모집단의 각 개체를 평가하고 적합성 점수를 할당하는 함수이다. 적합성 점수는 개체의 문자열이 목표(target) 문자열과 얼마나 비슷한 지를 나타낸다. 적합성 점수는 주어진 문제의 목표(target)가 무엇인지에 따라 달라진다. 마지막으로, 현재 모집단에서 가장 적합한 개체를 샘플링하여 자손을 생산하고 돌연변이시켜 새로운 모집단을 생성하는 함수다.

Listing 6.1 진화하는 문자열(계속)

num_generations = 100
population_size = 3000
str_len = len(target)
mutation_rate = 0.001 #J

pop_fit = []
pop = spawn_population(size=population_size, length=str_len) #init population

for gen in range(num_generations):
	pop, avg_fit = evaluate_population(pop, target)
	pop_fit.append(avg_fit) #record population average fitness
	new_pop = next_generation(pop, size=population_size, length=str_len, mut_rate=mutation_rate)
	pop = new_pop

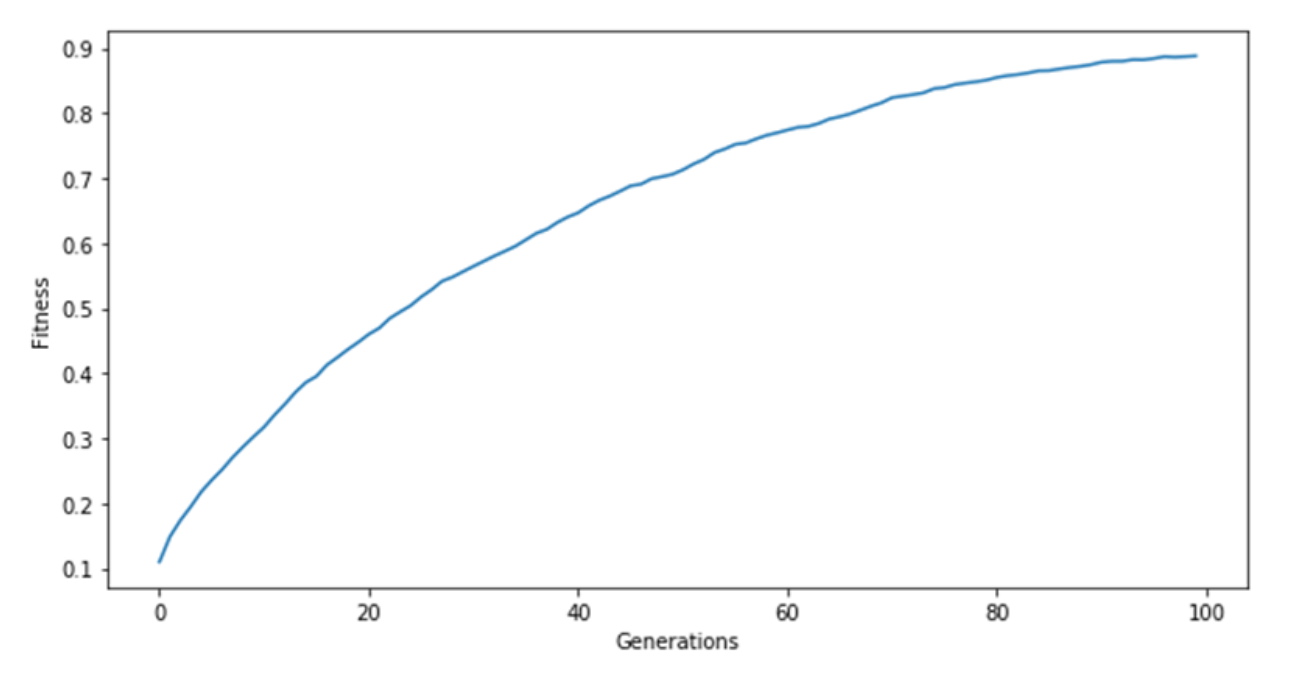
Figure 6.3: 이 표는 세대에 따른 모집단의 평균 적합성을 나타내는 도표이다. 평균 모집단 적합성은 단조 증가한 다음 안정기에 들어간다. 표가 들쭉날쭉하면 돌연변이 비율이 너무 높거나 모집단 크기가 너무 작기 때문일 수 있다. 표가 너무 빨리 수렴하면 돌연변이 비율이 너무 낮기 때문일 수 있다.

알고리즘을 실행하면 최신 CPU에서 몇 분이 걸리며 다음을 사용하여 모집단에서 가장 높은 순위의 개체를 찾을 수 있다.

>>> pop.sort(key=lambda x: x.fitness, reverse=True) #sort in place, highest fitness first
>>> pop[0].string
“Hello World!”

알고리즘이 동작했다! 이 문제는 문자열의 공간이 연속적이지 않기 때문에 실제로 진화 전략을 사용하여 최적화하기가 더 어렵다. 가장 작은 step에서 문자가 뒤집혀 지기 때문에 적당한 방향으로 작고 점진적인 단계를 수행하기가 어려운 것이다. 따라서 더 긴 목표 문자열을 만들고자 한다면 진화하는 데 훨씬 더 많은 시간과 리소스가 필요하다. 모델에서 매개 변수를 최적화 할 때 값이 약간 증가하는 것만으로도 적합성이 향상 될 수 있으며 이를 활용할 수 있다. 간단한 강화 학습 예제로 이 진화 전략이 어떻게 작동하는 지 보자. 에이전트가 Cartpole을 재생하도록 최적화하기 위해 진화 과정을 사용할 것이다. Policy function을 근사하는 신경망이라고 에이전트를 나타낼 수 있다. 에이전트는 State를 받아들이고 Action을 내보낸다. 아래에는 임의 가중치로 초기화된 3-계층 신경망의 예이다.

Listing 6.2 에이전트 정의

import numpy as np
import torch

agent_weights = [
	torch.rand(self.state_space, 10), # fc1 weights
	torch.rand(10), # fc1 bias
	torch.rand(10, 10), # fc2 weights
	torch.rand(10), # fc2 bias
	torch.rand(10, self.action_space), # fc3 weights
	torch.rand(self.action_space), # fc3 bias
]

def get_action_from_agent_weights(agent_weight, state):
	x = F.relu(torch.add(torch.mm(state, weights[0]), weights[1]))
	x = F.relu(torch.add(torch.mm(x, weights[2]), weights[3]))
	act_prob = F.softmax(torch.add(torch.mm(x, weights[4]), weights[5]))
	action = np.random.choice(range(len(act_prob)), p=act_prob)
	return action

PyTorch의 nn을 사용하지 않는다. 이전 섹션에서와 같이 nn.Sequential PyTorch의 모듈은 유용한 추상화를 제공하지만 모델의 기본 가중치를 쉽게 설정할 수는 없다. 이 부분은 나중에 이 Chapter의 뒤에서 알아본다. 가중치를 초기화하기 시작하고 모델을 통해 입력을 처리한 다음 출력에서 Action을 선택면 된다.

에이전트의 적합성을 확인하려면 환경을 통해 Policy를 실행하고 발생하는 총 Reward을 계산하면 된다. 변화량(variance)을 줄이고 보다 정확한 측정 값을 얻기 위해 여러 번 수행하여 평균을 구한다. 수행할 양이 많을 수록 적합성을 결정하는 데 시간이 오래 걸린다는 점을 명심한다.

Listing 6.3 정합성 정의

def get_fitness(self, env, agent_weights, max_episode_length, trial=5):
	total_reward = 0
	for _ in range(trials):
		observation = env.reset()
		for i in range(max_episode_length):
			action = agent(weights, observation)
			observation, reward, done, info = env.step(action)
			total_reward += reward
			if done:
				break
return total_reward / trials

6.2.2 가장 적합한 에이전트 선택하기

이제 한 에이전트가 다른 에이전트보다 적합한 때를 결정하는 방법을 알았다. 먼저 에이전트 집합을 만들고 (1 세대라고 함) 각 에이전트의 적합성을 평가한다.

Listing 6.4 1세대 에이전트 집합 만들기

first_generation = [init_random_agent_weights() for _ in range(generation_size)]

1 세대가 되면 가장 적합하지만 각 에이전트가 환경을 수행한 상위 2개 에이전트를 선택할 수 있다. 이것을 부모라고 부를 수 있다.

Listing 6.5 가장 적합한 에이전트 선택하기

top_agents_weights = sorted(agents_weights, reverse=True, key=lambda a: get_fitness(env, a))[:2]

6.2.3 새 에이전트를 생성하기 위해 에이전트 재결합하기

이제 가장 적합한 에이전트를 결정했으므로 가중치(weight)를 다음 세대로 전달하기 위해 다시 조합해야 한다. 이전에 재조합에 대해 살펴 봤지만 다시 한번 살펴 보자. 재조합(Recombination)은 “교차(Crossing)”또는 “짝짓기(Mating)”이라고도 하며 이러한 용어를 서로 바꾸어 사용할 것이다. 생물학적 용어로, 재조합되는 각 에이전트 또는 부모는 자손에게 전달될 DNA로 만들어진 유전자 집합을 가지고 있다. 각 부모는 전체 유전자를 전달시킬 수 없으며, 전부 전달하게 된다면 자손은 부모보다 두 배나 많은 유전자를 갖게 된다. 예를 들어 인간은 총 46 개, 23 쌍의 염색체(DNA 묶음)를 가지고 있다. 각 부모가 46 개의 염색체를 모두 자녀에게 전달하면 46 + 46 = 92 개의 염색체가 된다. 그리고 자손이 있다면 그 자손은 그 이상을 갖게된다. 이런일이 실제로 일어나지 않겠지만 너무 많은 염색체가 자손에게 전달되면 그 생명체는 생명을 유지하기 힘들다. 대신에 각 부모는 유전자의 절반, 집합당 염색체 1 개를 제공한다. 그렇게 되면 자손은 부모의 유전자로 부터 각각 절반을 가질 것이다.

우리의 인공 에이전트는 비슷한 패턴을 따른다. 이 경우 유전자는 우리 신경망의 가중치(weight)가 될 것이고 각 층(Layer)은 염색체로 간주 될 수 있다. 우리는 각 부모 유전자의 정확히 절반을 자녀에게 전달할 필요는 없다. 부모 A에서 1/3, 부모 B에서 2/3, 부모 A에서 4/5, 부모 B에서 1/5를 전달할 수 있다. 문제는 각 부모로부터 어떤 유전자가 자녀에게 전달될지 모르기 때문에 본질적으로 무작위로 선택해야 한다는 것이다. 이렇게 되면 각 부모는 자손에게 자신의 가중치를 전달 할 수 있는 기회를 가지게 된다.

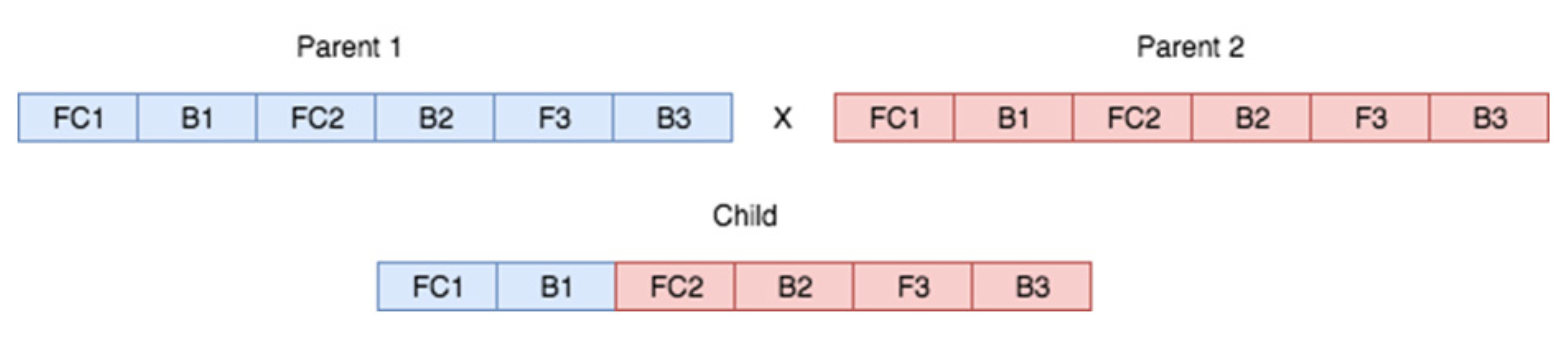
Figure 6.4: 각 부모의 각 가중치를 각 자손에게 전달한다. 각 자손은 각 부모로부터 임의의 가중치를 받는다. 위의 경우 자손은 부모 1에서 처음 두 “유전자”(FC1 및 B1)를 받고 부모 2에서 나머지 4 개를 받았지만 이는 무작위 순열(Permutation) 일 수 있다.

다음은 두 에이전트의 짝짓기 (교차) 코드 구현이다. 우리는 무작위로 0과 crossover_idx라는 총 가중치 수 사이의 난수를 생성하며 자손은 부모 A의 crossover_idx 이전의 모든 유전자와 부모 B의 crossover_idx 이후의 모든 유전자를 상속한다.

Listing 6.6 교차(Crossing)

def cross(agent1_weights, agent2_weights, agent_config):
	num params = len(agent1 weights)
	crossover_idx = np.random.randint(0, num_params)
	new_weights = agent1.weights[:crossover_idx] + agent2.weights[crossover_idx:]
	num_params_to_update = np.random.randint(0, num params) # num of params to change
	return new_weights

6.2.4 돌연변이 도입

돌연변이는 진화에 있어서 중요하다. 생물학에서 돌연변이는 유기체 DNA의 무작위 변화이다. 이것은 때때로 이전 세대에서 보여지지 않은 새로운 특성으로 이어진다. 돌연변이가 없다면 우리는 조상의 동일한 유전자를 단지 뒤섞을 뿐일 것이다. 예를 들어, 부모 1이 유전자 FC1 및 B1을 보유하고 부모 2가 유전자 FC2 및 B2를 보유했다고 가정하자. 번식(breeding)시에, 돌연변이가 가능하지 않은 경우, 얼마나 많은 자손을 가지고 있는지에 관계없이 4 개의 다른 유전자 집합만 가질 수 있다. 돌연변이는 모집단에 변화량(variance)를 추가하여 새로운 정보를 만들 수 있다.

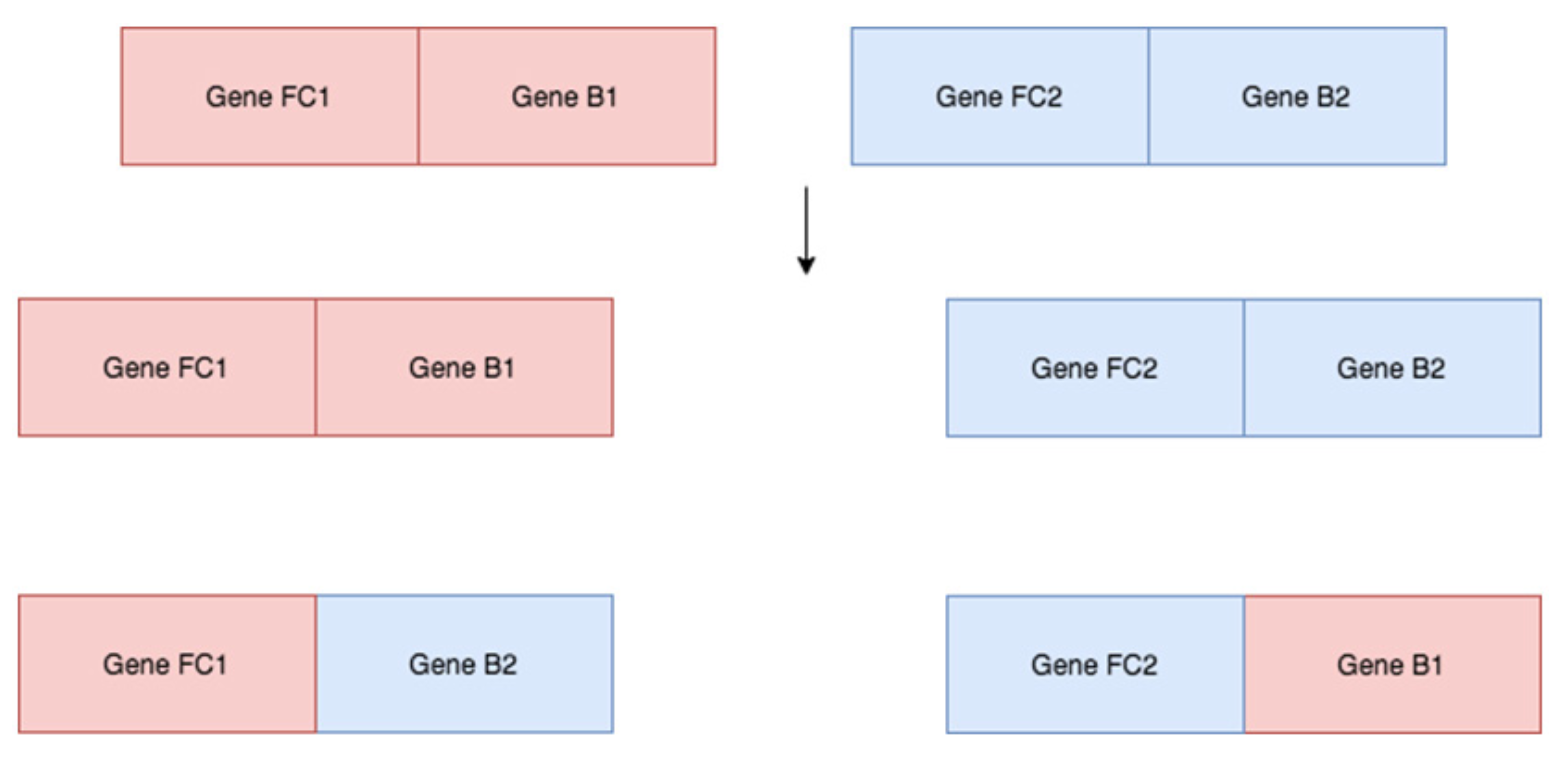
Figure 6.5: 만약 두 부모가 오직 두 개의 유전자를 가지고 있다면 오직 4가지 서로 다른 타입의 자손만이 있을 수 있다.

모든 자손에게 존재하는 동일한 유전자가 부모에게 존재했기 때문에 더 많은 세대의 번식에도 아무런 의미가 없다. Figure 6.4에서 보여 주듯이 6개의 유전자에 대해서 64(2^6) 명의 유전자가 서로 다른 자손이 생길 수 있다. 그러나 큰 규모의 모집단으로 시작하지 않으면 각 세대에서 충분한 차이를 만들어 일부 자손이 다른 자손보다 두드러지게 되는 결과를 내기는 매우 어렵다.

돌연변이를 통해 우리는 다양성이 많은 모집단을 생성 할 수 있다. 두 부모가 자손을 낳기 위해 짝짓기 할 때, 돌연변이 과정 후를 예단할 수 있는 에이전트를 만들어 내는 것은 아니다.

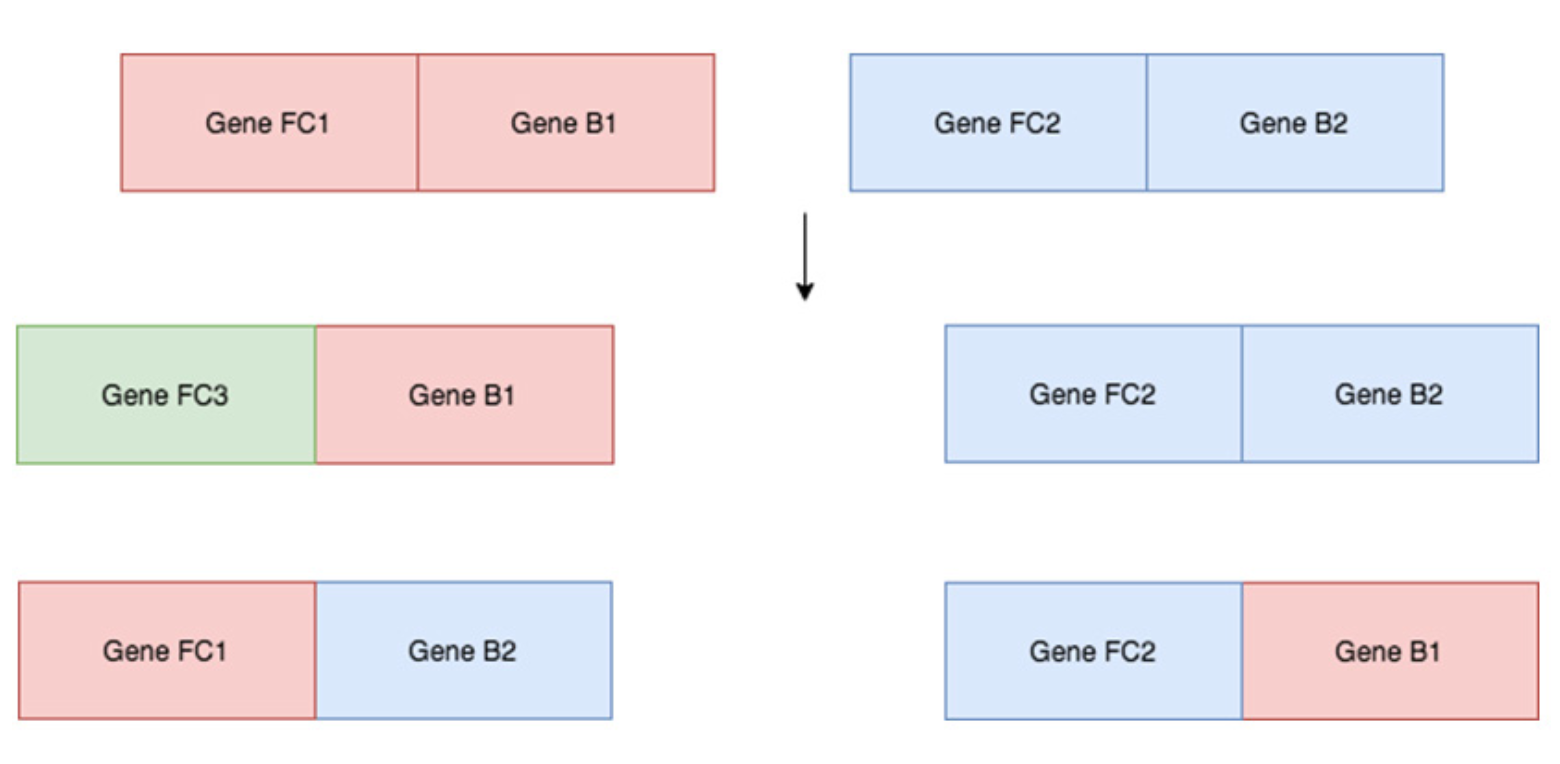
Figure 6.6: 돌연변이는 각 세대에 무작위로 도입된다. 돌연변이가 없으면 자손의 조합을 쉽게 결정할 수 있다.

Figure 6.6에서 볼 수 있듯이 돌연변이가 도입되면 예상하지 못한 새로운 유전자 변형이 형성 될 가능성이 있다. 변형된 유전자는 미래 세대에게 전달 될 수 있고 미래 세대마다 더 많은 돌연변이를 유발할 수있는 기회를 가지게 된다! 그러나 중요한 것은 돌연변이가 낮은 속도로 발생하며 작은 변화만 유발한다는 것이다. 단일 돌연변이는 임의의 매개 변수 집합을 사용하지 않고 완벽하게 최적화된 매개 변수로 변환하지 않는다. 그러나 약간의 작은 돌연변이가 매개 변수를 합산하여 최적에 약간 더 가깝게 만들 수 있다. 이것이 코드에서 어떻게 보이는지 알아보자. 이렇게 하려면 에이전트의 가중치를 취하고 수정하려는 가중치 수를 임의로 생성한다. 수정하려는 각 가중치에 대해 임의의 노이즈를 추가한다.

Listing 6.7 돌연변이

def mutate(new_weights):
	num_params_to_update = np.random.randint(0, num_params) # num of params to change
	for i in range(num_params_to_update):
		n = np.random.randint(0, num_params)
		new_weights[n] = new_weights[n] + torch.rand(new_weights[n].size())
	return new_weights

6.2.5 돌연변이는 여러 세대에 걸쳐 일어난다.

생물학에서 각 돌연변이는 매우 미묘하여 유기체의 특성을 변화시켜 한 세대를 다른 세대와 구별하기가 어려울 수 있다. 그러나 여러 세대를 거치는 과정으로, 이러한 돌연변이와 변화량이 축적되어 지각 가능한 변화를 허용한다. 이전에 이야기했던 새 부리 예제를 사용해 봅시다. 처음에 모든 새들은 대략 같은 부리 모양을 가졌다. 그러나 세대가 발생함에 따라 무작위 돌연변이가 집단에 도입되었다. 다시 말하지만, 이러한 돌연변이의 대부분은 아마도 새들에게 전혀 영향을 미치지 않았거나 심지어 해로운 영향을 미쳤다. 그러나 인구가 충분하고 세대가 많으면 부리 모양에 유리하게 영향을 미치는 무작위 돌연변이가 발생한다. 그 새들은 다른 새들보다 식량을 얻는 데 유리할 것이므로 유전자를 전달시킬 가능성이 더 높다. 따라서, 다음 세대는 유리하게 형성된 부리 유전자의 빈도가 증가 할 것이다. 새에 대해서는 충분히 말했으니, 이제 강화 학습 에이전트로 돌아간다. 돌연변이는 에이전트 모집단의 성능 차이를 증가시킨다. 돌연변이는 무작위적이며 환경에 체계적인 탐색이 필요하기 때문에 이러한 변화의 대부분은 에이전트의 적합성에 크게 영향을 미치지 않거나 에이전트가 부모보다 성능이 저하되지 않는다.

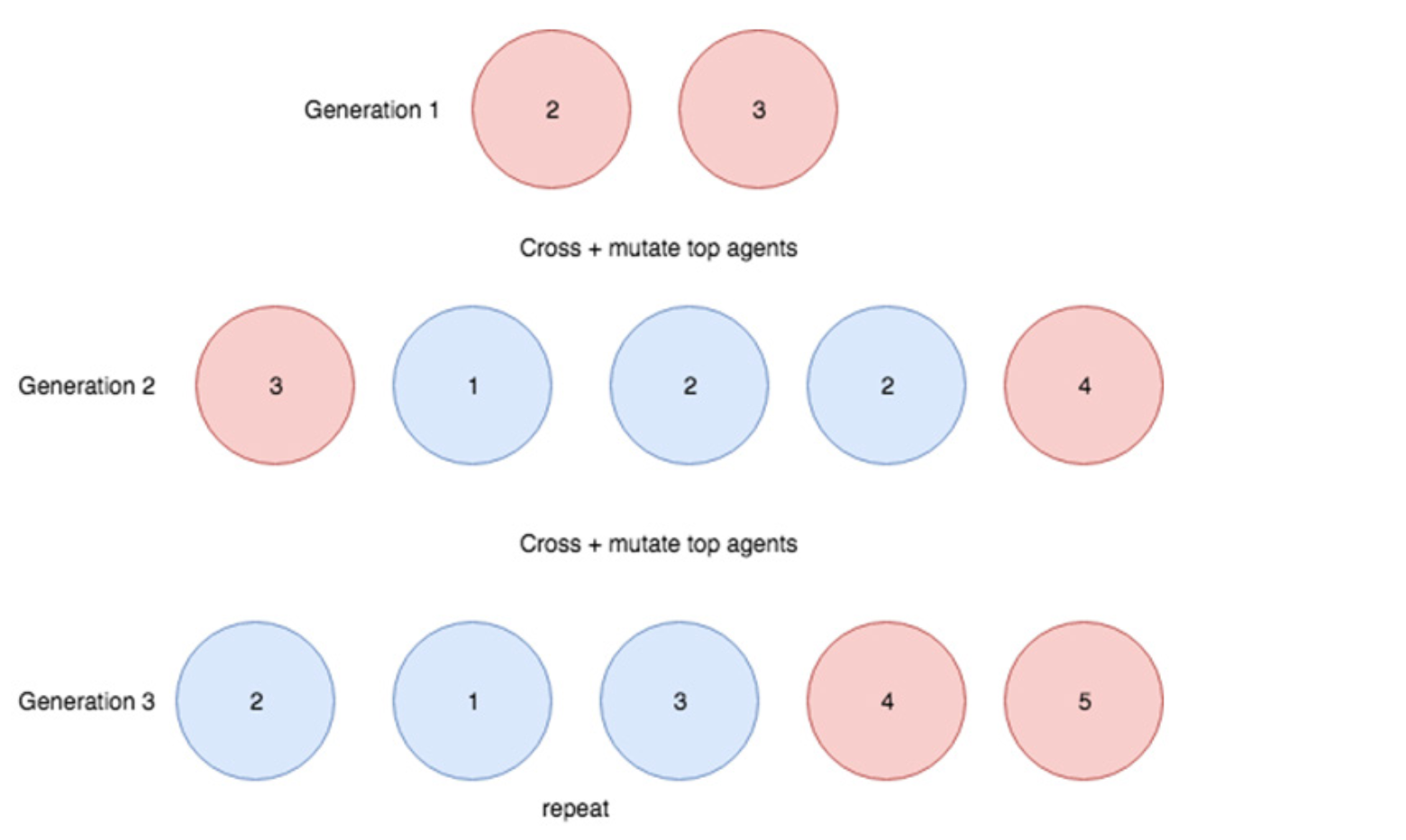
Figure 6.7: 자연 선택에 의한 진화의 원리를 보여주는 다이어그램. 숫자는 에이전트의 적합성을 나타내고 빨간색 에이전트는 다음 세대를 생성하도록 선택된 상위 항목이다. 각 세대는 부모로부터 파생 된 재조합 특성을 가진 자손을 생산한다. 교차와 돌연변이가 무작위이기 때문에 모든 자손이 부모보다 더 적합하지는 않다. 더 적합한 개체가 교차할 가능성이 높은 과정으로 전체 인구의 적합성이 세대에서 세대로 증가한다.

그러나 모집단 규모와 세대가 충분하면 부모보다 약간 더 나은 자손이 나오게 만든다.

6.2.6 전체 학습 루프

모든 단계를 검토해 봅시다. 먼저 1 세대 에이전트를 시작해야 한다. 그런 다음 상위 2 개의 에이전트를 선택하고 돌연변이를 도입하여 차세대를 생성한다. 그 다음 세대부터 우리는 상위 2 명의 부모를 선택하고 최고 에이전트가 생산 될 때까지 반복한다.

Figure 6.8: 강화 학습 에이전트의 진화 최적화를 위한 전체 학습 루프.

아래는 전체 학습 루프이다. 원하는 적합성을 가진 에이전트가 확보될 때까지 이 루프를 반복한다.

Listing 6.8 전체 학습 루프

n_generations = 100
generation_size = 20
generation_fitness = []

env = gym.make('CartPole-v1')
max_fitness = 0

agents = [init_random_agent_weights(), init_random_agent_weights()]

for i in range(n_generations):
	next_generation = reproduce(env, agents, generation_size)
  ranked_generation = sorted([get_fitness(env, a) for a in next_generation], reverse=True)
	avg_fitness = (ranked_generation[0] + ranked_generation[1]) / 2
	generation_fitness.append(avg fitness)
	agents = next_generation

위의 코드를 실행하고 결과가 어떻게 나오는지 보자.

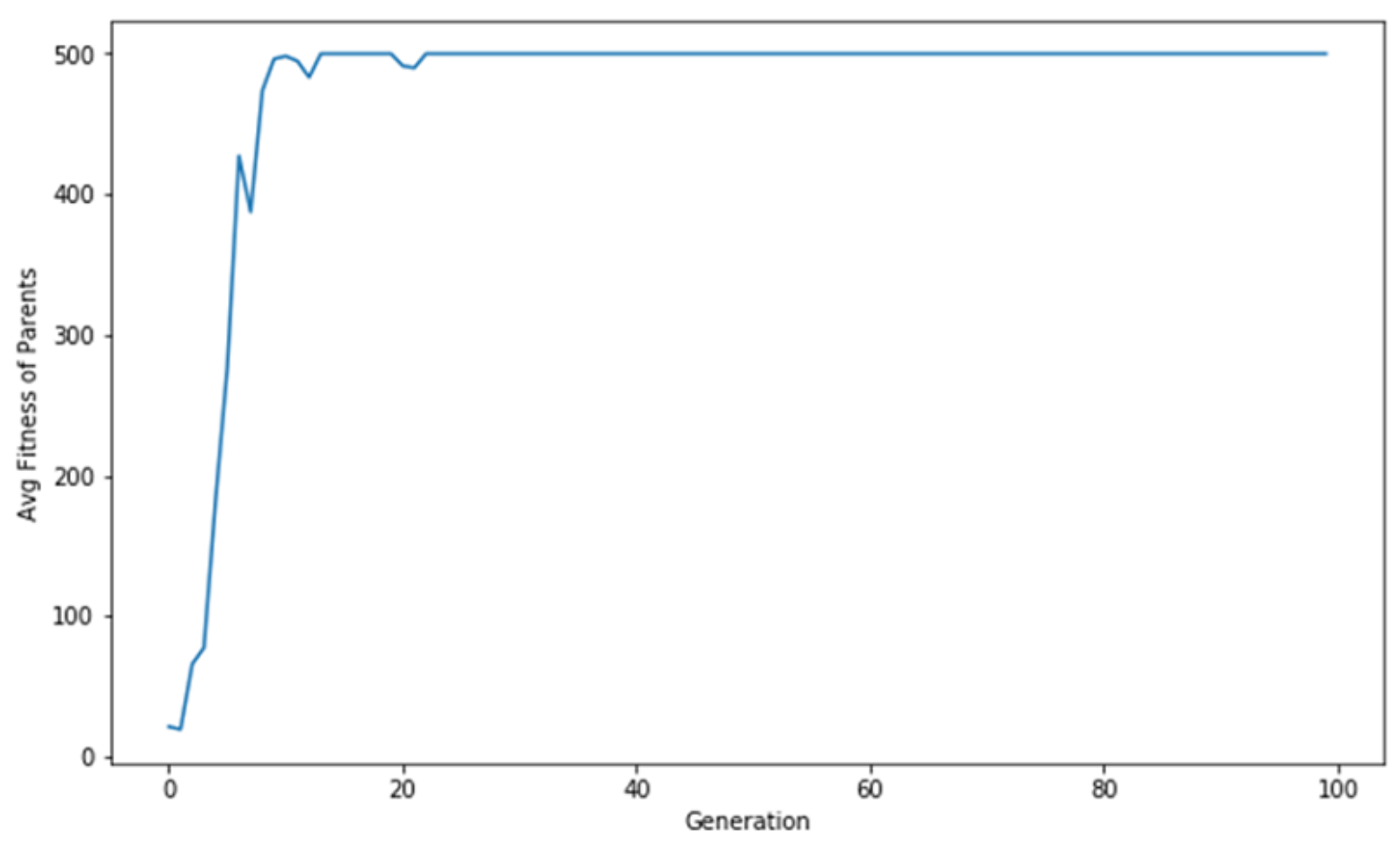
Figure 6.9. 세대가 증가함에 따라 개체의 평균 적합도가 증가하다 Optimization 값에 수렴함.

방금 우리는 자연 선택(natural selection)을 모방한 알고리즘을 만들었다. 위에서 볼 수 있듯이 몇 세대의 에이전트를 생성 한 후 환경에서 보상을 극대화 할 수있는 에이전트를 생성했다. 진화 전략의 단점 중 하나는 그라디언트 기반 최적화 알고리즘을 사용하는 것보다 환경을 통해 에이전트를 훨씬 더 많이 실행해야 한다는 것이다. 다음 섹션에서는 이 접근법의 몇 가지 장단점에 대해 논의 할 것이다.

6.3 진화 알고리즘의 장단점

위에서 본 것처럼 구현한 진화 알고리즘은 이전 방식과 약간 다르다. ES(Evolutionary Strategies) 접근법이 더 잘 작동하는 상황과 그렇지 않은 상황이 있다.

6.3.1 진화 알고리즘 좀 더 탐구해 보자

그라디언트 없는(Gradient-free) 접근 방식의 한 가지 장점은 그라디언트 기반(Gradient-based) 접근 방식보다 더 많이 탐색(explore more)하는 경향이 있다는 것이다. DQN과 PG 모두 비슷한 전략을 따른다. 경험을 수집하고 에이전트에게 더 많은 Reward을 제공하는 Action을 취하도록 한다. 이전에 논의한 바와 같이, 이로 인해 에이전트가 하나의 Action를 선호한다는 것을 알면 에이전트는 새로운 State 탐색을 포기하는 경향이 있다. 우리는 epsilon-greedy Policy을 통합하여 DQN으로 이 문제를 해결했다. 즉, 심지어 선호하는 Action이 있는 때에도 무작위(Random) Action을 취하게 하는 경우를 줄였다. Stochastic Policy Gradient를 사용하여 모델이 출력한 Action Probability 벡터로부터 다양한 Action을 취했다. 다른 한편으로, 유전자 알고리즘의 에이전트는 어떤 방향으로도 몰아대지 않는다. 각 세대마다 많은 에이전트를 생성하고 있으며, 그 사이에 많은 변형이 있으므로 대부분 서로 다른 Policy를 갖는다.

6.3.2 진화 알고리즘은 매우 샘플 집약적이다

위 코드에서 알 수 있듯이 각 에이전트는 환경에서 5회 실행하여 적합성을 결정해야 한다. 또한 세대당 10개의 에이전트가 있다. 즉, 점진적으로 개선된 에이전트를 생성하려면 환경에서 50번 실행해야 한다. 그라디언트 기반 방법과 비교할 때, 진화 알고리즘은 에이전트의 가중치를 전략적으로 조정하지 않고 많은 에이전트를 생성하고 도입하면서 임의의 돌연변이 / 교차를 통해서 유리하게 진화되기를 바라고 있기 때문에 샘플 지향적 경향이 있다. 진화 알고리즘은 DQN 또는 PG 방법보다 데이터 효율성이 떨어진다(less data-efficient)고 말할 수 있다.

적합성을 결정하는 데 필요한 에피소드 수를 5에서 작은 수로 줄일 수 있다. 그러나 시행 횟수가 적을수록 계산되는 적합성 값에는 더 많은 변화량(variance)가 있게 된다. 우리는 에이전트가 환경의 다른 State에서도 잘 일반화되기를 원하며 환경을 여러 번 실행하는 것이 더 정확한 방법임을 기억하자. 예를 들어 에이전트가 환경을 한 번만 실행하도록 요구한 경우 한 번 실행 한 결과에 따라 예상 적합성을 계산한다. 이 경우 일반화가 덜된 에이전트가 될 수 있지만 높은 적합성을 얻기 위한 매우 좋은 위치로 초기화되었을 수도 있다. 이후 에이전트가 일반적으로 더 적합하다고 잘못 판단하여 이를 부모로 선택하고 성능이 좋지 않은 과적합된(overfitted) 가중치를 다음 세대에 전달한다. 이것은 더 나은 에이전트를 생산하기 위해 더 많은 세대가 필요하다는 것을 의미하며, 결국 더 많은 시간을 환경에서 실행해야 한다.

부모 에이전트를 적게 생산할 수 있도록 모집단 규모를 줄이고 싶다고 가정해 보자. 모집단 규모를 줄이면 두 부모를 선택할 때 선택할 에이전트가 적어진다. 이것은 덜 적합한 개체가 다음 세대로 만들어 질 가능성이 높다. 더 나은 적합성으로 이끄는 조합을 찾기 위해 많은 수의 에이전트를 생산하고 있다. 또한 생물학에서와 같이 대부분의 경우 돌연변이는 부정적인 영향을 미치며 적합성을 악화시킨다. 더 큰 모집단 크기를 가지면 우리가 도입한 돌연변이가 유익한 효과를 가질 확률이 높아진다. 로봇 공학이나 자율 주행차와 같이 데이터 수집 비용이 비싸면 데이터 비효율성(data inefficiency)이 문제가 된다. 로봇이 한 에피소드의 데이터를 수집하는 데 보통 몇 분이 걸리며, 우리는 과거 알고리즘에서 간단한 에이전트를 훈련시키는 데 수천 개의 에피소드가 아니라면 수백이 걸린다는 것을 알고 있다. 자율 주행 차량이 State 공간 (실세계)을 충분히 탐색하기 위해 얼마나 많은 에피소드가 필요할지 상상해 보라. 로봇을 구매하고 유지 보수를 수행해야하기 때문에 시간이 많이 걸리는 것 외에도 물리 에이전트 학습은 훨씬 더 비싸다. 이상적으로, 에이전트에게 물리적 바디를 제공하지 않고도 학습시킬 수 있다.

6.3.3 시뮬레이터

시뮬레이터는 위에 나열된 문제를 해결한다. 값 비싼 로봇을 사용하거나 필요한 센서가 장착된 자동차를 만드는 대신 환경이 제공하는 경험을 모방하는 컴퓨터 소프트웨어를 사용할 수 있다. 예를 들어, 자동차에 필요한 센서를 장착하고 실제 자동차에 모델을 배치하는 대신 자율 주행 자동차를 운전하도록 에이전트를 학습 할 때 운전 게임 Grand Theft Auto(운전 시뮬레이터)와 같은 소프트웨어 환경 내에서 에이전트를 학습 할 수 있다. 에이전트는 주변 이미지를 입력으로 수신하고 가능한 한 안전하게 프로그램된 목적지로 차량을 가져 오는 운전 Action을 출력하도록 학습된다.

Figure 6.10: 비디오 게임인 Grand Theft Auto는 처음에 자율 주행 엔지니어가 모델을 테스트하는 데 사용했다. 모델은 주변의 이미지를 수신하고 운전 Action을 출력한다.

시뮬레이터에서 에이전트를 학습하는 것이 훨씬 저렴할뿐만 아니라 에이전트는 실제보다 훨씬 빠르게 환경과 상호 작용할 수 있기 때문에 훨씬 빨리 학습 할 수 있다. 2시간 분량의 영화를 보고 이해하려면 2시간이 소요된다. 보다 집중적으로 초점을 맞추면 재생 시간을 2 또는 3으로 늘려 필요한 시간을 1시간 이하로 줄일 수 있다. 반면에 컴퓨터는 첫 번째 작업을 마치기 전에 완료 할 수 있다. 컴퓨터의 크기에 따라 ResNet-50을 실행하는 8 개의 GPU 컴퓨터 (Amazon AWS의 경우 p3.16x 대형)는 초당 700 개가 넘는 이미지를 처리 ​​할 수 ​​있다. 초당 24 프레임 (할리우드 표준)으로 실행되는 2시간짜리 영화에는 처리해야 할 172,800 개의 프레임이 있다. 완료하는 데 4 분이 걸린다. 또한 몇 프레임마다 드롭하여 딥 러닝 모델의 재생 속도를 효과적으로 높일 수 있어 처리 시간이 2 분 미만으로 줄어 든다. 또한 처리 능력을 높이기 위해 더 많은 컴퓨터를 문제에 던질 수 있다. 보다 최근의 강화 학습 예제를 위해 OpenAI Five 봇은 매일 180년 동안 Dota 2 게임을 할 수 있었다. 컴퓨터가 처리 할 수있는 것보다 더 빠르게 처리 할 수 ​​있기 때문이고 이것이 시뮬레이터가 중요한 이유이다.

6.4 진화 전략은 병렬화가 가능하다

병렬 처리 vs 직렬 처리, 스케일링 효율성, 노드 간 통신 및 다양한 스케일링 접근 방식을 논의하면서 확장 가능한 대안으로 진화 전략에 대해 살펴 보겠다.

6.4.1 확장 가능한 대안으로서의 진화 전략

ES 에이전트 교육이 더 빠를 수있는 또 다른 이유는 알고리즘을 매우 효율적으로 확장 할 수 있기 때문이다. 2017 년 OpenAI는 강화 학습의 확장 가능한 대안으로 진화 전략이라고하는 논문을 발표했다.이 보고서에서는 더 많은 기계를 추가하여 에이전트를 매우 신속하게 효율적으로 학습 할 수 있었다. CPU 코어가 18개인 단일 컴퓨터에서 3D 휴머노이드가 11 시간 안에 걷는 법을 익힐 수 있었다. 그러나 80대의 머신(1440 CPU 코어)으로는 10분 안에 에이전트를 생성 할 수 있었다!

Figure 6.11: OpenAI Gym 라이브러리에서 제공하는 3D 휴머노이드 환경. 이것은 휴머노이드가 앞으로 나아가는 것이 목표인 높은 차원의 문제이다. ES는 한 대의 컴퓨터로 11시간 만에 이 문제를 “해결”할 수 있었지만 80대의 컴퓨터를 사용했을 때는 10분 안에 에이전트를 생성 할 수 있었다.

물론, 이 문제를 해결하기 위해 많은 머신과 돈을 투입했었다. 그러나 이 문제는 실제로는 생각보다 더 까다로운 데다가 다른 그라디언트 기반 접근 방식은 여러대의 머신으로 확장하기 어렵다. 이러한 방법이 어떻게 확장되는 지에 대한 차이점을 알아보기 전에 머신 러닝 알고리즘이 어떻게 확장되는 지에 대해 먼저 설명한다.

6.4.2 Parallel 처리 vs Serial 처리

위의 예에서 각 세대에서 가장 적합한 에이전트를 결정할 때 다음 실행을 시작하기 전에 각 에이전트가 환경에서 완전히 실행할 때까지 기다려야 했다. 에이전트가 환경을 통과하는 데 30초가 걸리고 적합성을 결정하는 10개의 에이전트가 있는 경우 5분이 소요된다.

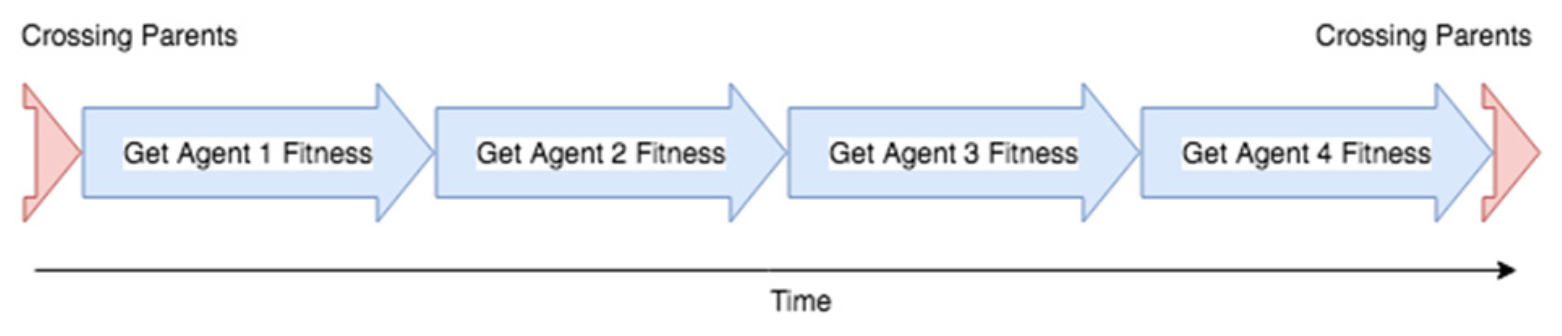
Figure 6.12: 현재 Computational Complexity. 에이전트의 적합성을 결정하는 것은 종종 학습 과정에서 가장 느리게 진행되며 환경을 통해 에이전트를 실행해야한다 (아마도 여러 번). 단일 컴퓨터에서 이 작업을 수행하는 경우 이 작업을 직렬로 수행한다. 즉, 두 번째 에이전트의 에이전트 결정을 시작하기 전에 환경을 통한 실행이 완료 될 때까지 기다려야 한다.

이런 방식의 프로그램을 ‘Serial’ 이라고 알려져 있다. 각 에이전트의 적합성을 결정하는 것은 일반적으로 ES 전략에서 시간이 가장 오래 걸리는 작업이지만 각 에이전트는 서로 독립적으로 자신의 적합성을 평가할 수 있다. ‘Serial’ 방식 대신에 세대의 각 에이전트를 여러 컴퓨터에서 동시에 실행할 수 있다. 10개의 에이전트는 각각 10개의 머신을 사용하며 동시에 적합성을 결정할 수 있다. 즉, 한 대의 컴퓨터에서 실행하는 경우 5배가 아니라 10배의 속도로 한 세대를 완료하면 ~30초가 소요된다. 이와 같은 방식의 프로세스를 ‘Parallel’ 이라고 알려져 있다.

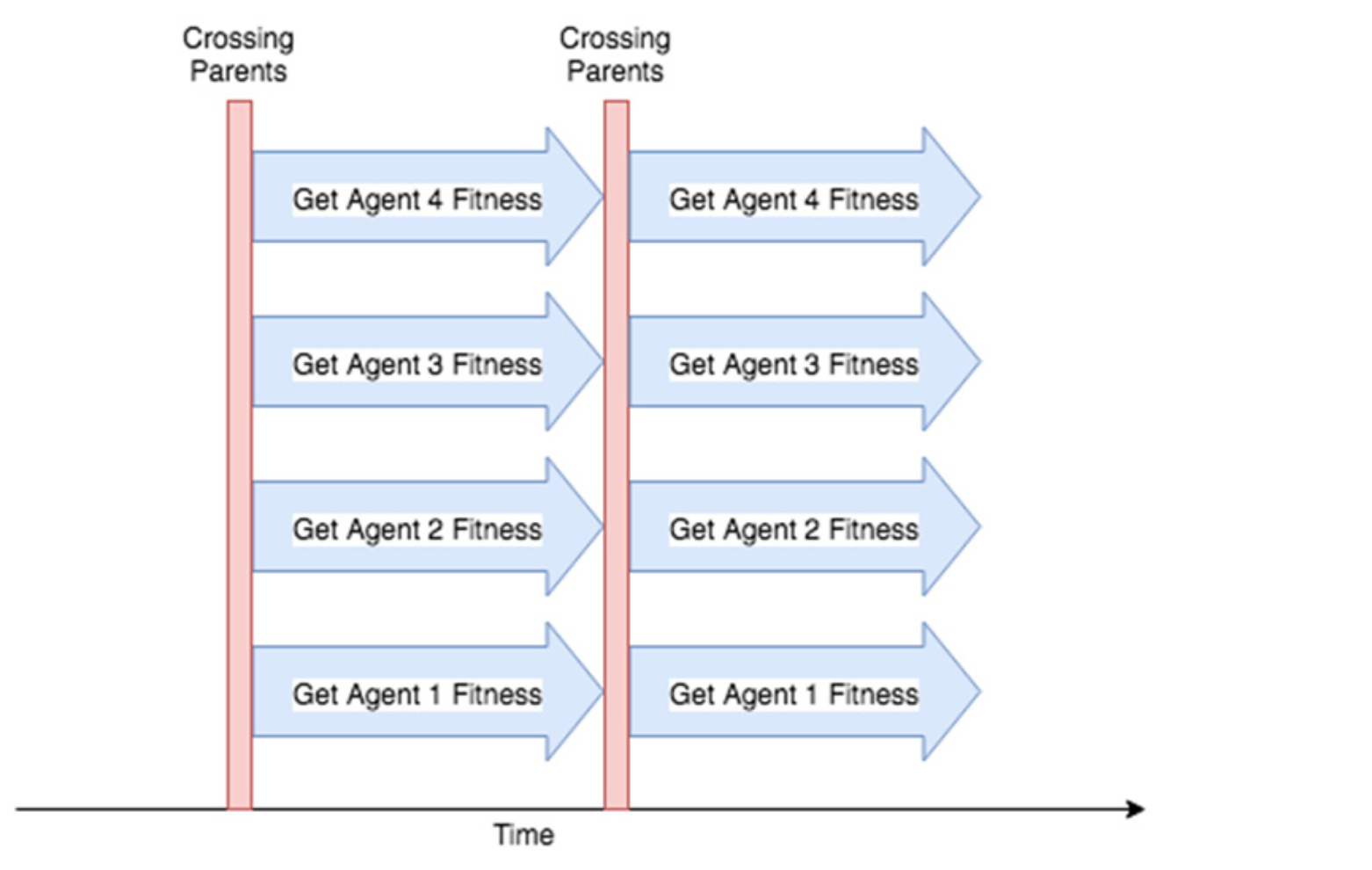
Figure 6.13: 배치상 여러 대의 머신이 있는 경우 각 머신의 각 에이전트의 적합성을 서로 병렬로 결정할 수 있다. 다음 에이전트를 시작하기 전에 한 에이전트가 환경에서 실행하여 완료 할 때까지 기다릴 필요가 없다. 이 장점이 에피소드 길이가 긴 에이전트를 교육하는 경우 속도의 향상을 가져오게 된다.

6.4.3 확장 효율(Scaling Efficiency)

그래서 우리는 문제를 해결하기 위해 더 많은 머신과 돈을 투입할 수 있으며 많은 시간을 기다릴 필요가 없어졌다. 위의 가상의 예에서 우리는 10개의 머신를 추가하여 10배의 속도를 올렸다. 이것은 확장 효율이 1.0 인 경우다. 확장 효율성은 더 많은 리소스가 투입 될 때 특정 접근 방식이 어떻게 개선되는 지를 설명하는 데 사용되는 용어로 아래와 같이 계산할 수 있다.

그러나 실제 환경에서는 프로세스의 확장 효율성이 절대로 1이 되지 않는다. 효율성을 감소시키는 머신을 추가하는 데는 항상 추가 비용이 있다. 보다 현실적으로 10개의 기계를 추가하면 속도가 9배 증가한다. 위의 확장 효율 방정식을 사용하여 스케일링 효율을 0.9로 계산할 수 있다(이 정도면 실제로 꽤 좋은 것임). 이제 우리의 진화 사례로 돌아가 봅시다. Figure 6.13과 같이 하나의 머신은 최고의 에이전트를 선택하는데 사용하고 다른 머신은 적합성을 결정하는데 사용하도록 구현할 수 있다.

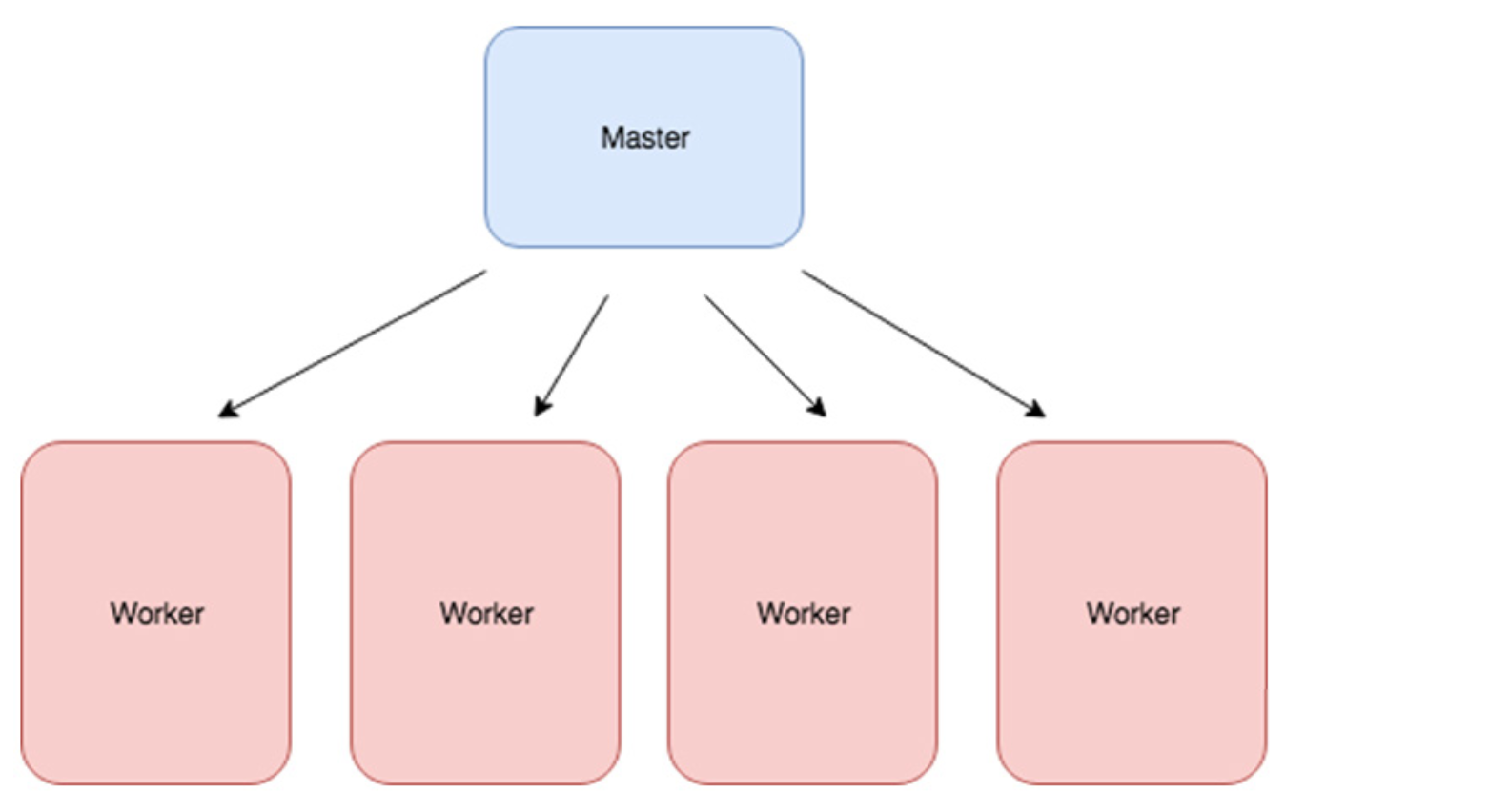
Figure 6.14: ES 알고리즘을 여러 시스템에 배포하는 방법에 대한 토폴로지. 선택 프로세스를 수행하는 하나의 머신(“마스터” 노드라고 함)과 에이전트의 적합성을 결정하는 n개의 머신이 있다.

모든 단계는 머신 간에 통신하는 데 약간의 네트워크 시간이 필요하며 이는 단일 머신에서 모든 것을 실행하는 경우 발생하지 않는다. 또한 마스터(Master) 노드에서 “Crossing parents” 단계를 시작하려면 모든 작업자(Worker) 노드에서 각 에이전트의 적합성을 계산해야 한다. 다른 머신보다 속도가 느린 머신이 하나만 있더라도 다른 작업자 노드는 기다려야 한다.

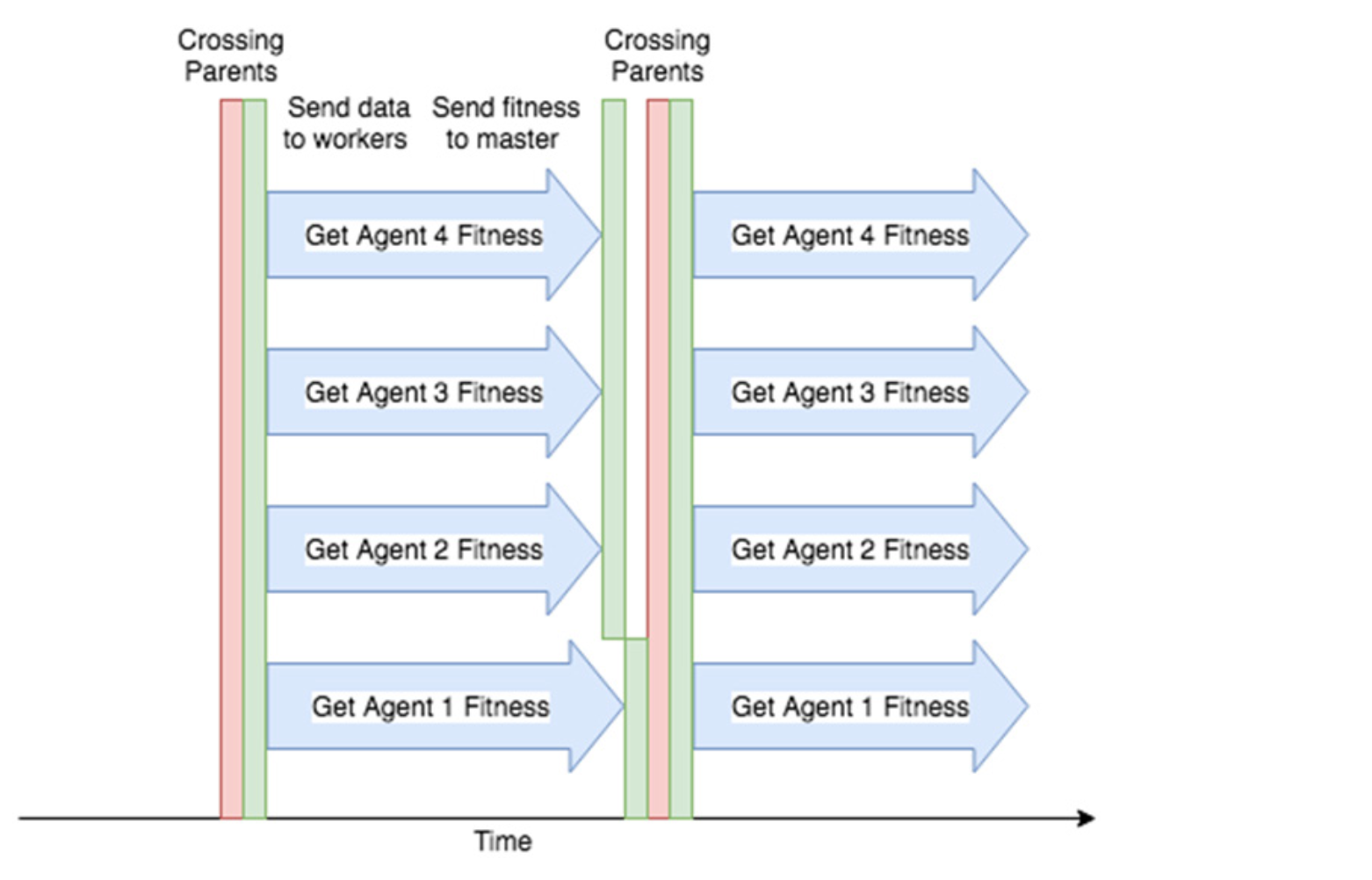
Figure 6.15: 비효율성을 소개하는 Figure 6.12의 수정된 뷰. 녹색 막대는 마스터 노드 및 작업자 노드가 서로 통신하는 데 걸리는 네트워크 시간을 나타낸다. 또한 에이전트 1과 같이 다른 작업자 노드 보다 느린 작업자 노드가 있으면 다른 작업자 노드는 기다려야 한다.

6.4.5 두 숫자만 보내기

그래서 마스터 노드 만이 어떤 에이전트가 부모인지 알고 있으며 다음 세대를 생성하기 위해서는 해당 정보가 필요요하다. 각 작업자 노드가 동일한 에이전트를 모두 가지고 있고 마스터 노드는 어떤 에이전트가 부모인지 커뮤니케이션하는 것에만 책임이 있는 경우 어떻게 해야 할까?

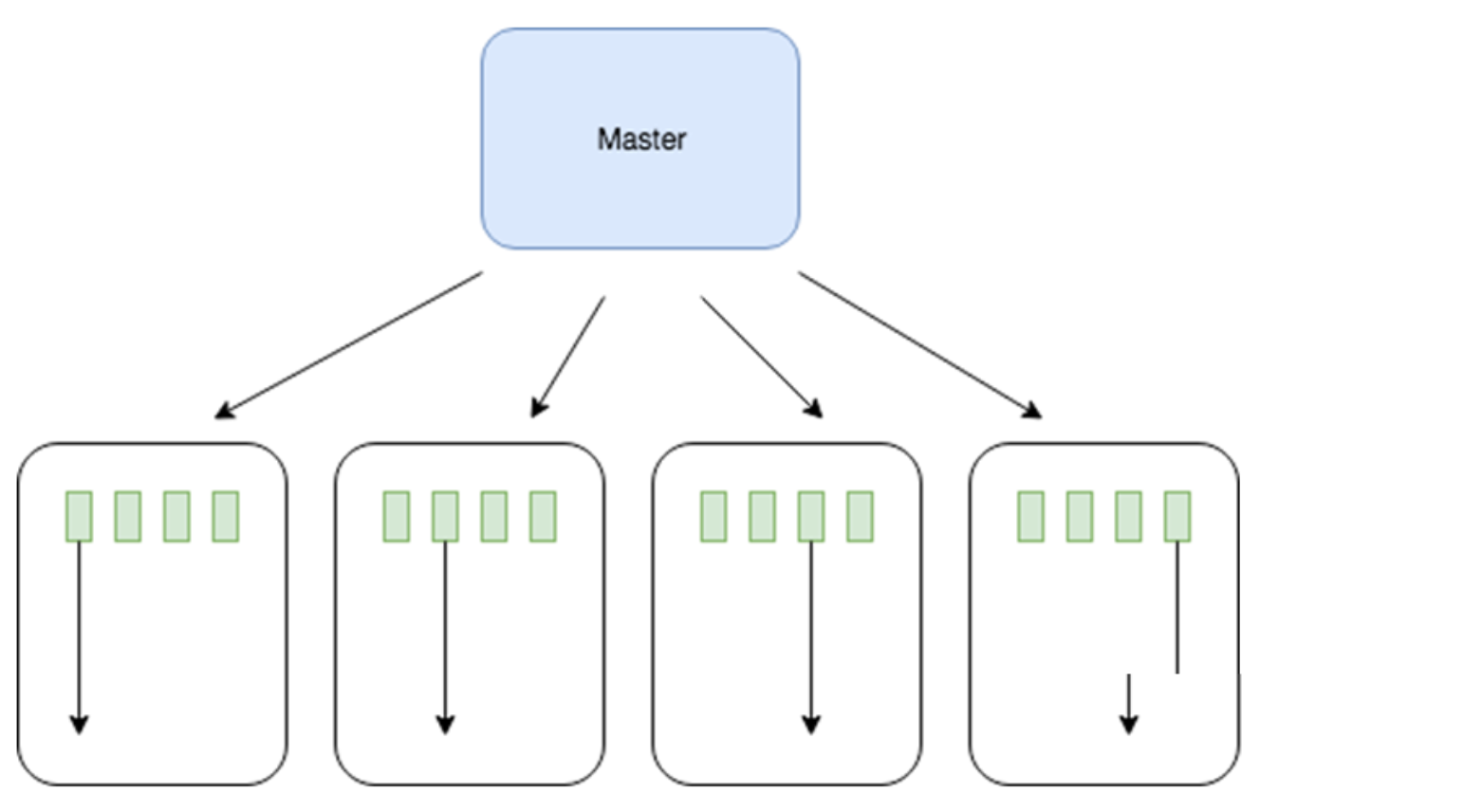
Figure 6.16: OpenAI의 분산 ES 논문에서 파생 된 아키텍처. 각 작업자 노드는 모든 에이전트의 모든 가중치를 포함하지만 일부 모집단의 적합성을 평가할 책임이 있다. 그런 다음 에이전트의 적합성 점수를 마스터 노드에게 보내고 마스터 노드는 가장 적합한 에이전트(부모)의 위치를 작업자에게 다시 보내게 된다. 작업자 노드는 다음 세대를 생산하고 이 과정을 반복한다.

우리는 부모 1과 부모 2를 식별하는 각 작업자 노드에게 두 개의 숫자만 보내면 된다. 부모의 신원을 알고있는 작업자 노드는 다음 세대를 생산할 책임이 있으며 이는 상대적으로 계산이 적게 드는 작업이다. 약간의 문제점이 있다. 각 작업자 노드는 서로 동일한 세대를 생산해야 한다. 이 장에서 쭉 언급했던 바와 같이 에이전트들이 부모의 가중치를 가지고 있지만, 무작위성(randomness)과 깊이 관련되어 있다. 다음 세대의 각 자손에 대해 우리는 무작위로 교차 유전자의 수인 crossover_idx를 무작위로 생성한 다음 무작위 노이즈를 추가하여 유전자를 돌연변이시킨다. 다행히도 이 무작위성에 대한 해결책이 이미 있다.

6.4.6 시딩(Seeding)

시딩을 사용하면 매번 다른 컴퓨터에서도 동일한 난수를 일관되게 생성 할 수 있다. 다음 코드를 실행하면 위의 숫자가 “임의로”생성 되더라도 아래에 표시된 것과 동일한 결과가 표시된다.

Listing 6.9 시딩(Seeding)

import numpy as np
np.random.seed(10)
np.random.rand(4)
>>> array([0.77132064, 0.02075195, 0.63364823, 0.74880388])

np.random.seed(10)
np.random.rand(4)
>>> array([0.77132064, 0.02075195, 0.63364823, 0.74880388])

시딩은 다른 연구자들이 재현할 수 있도록 하여 난수와 관련된 실험을 다시 복제 할 수 있도록 해 준다. 명시적 시드를 제공하지 않으면 일반적으로 시스템 시간 또는 다른 종류의 변수 번호가 사용된다. 예를들어 새로운 RL 알고리즘을 개발했다면 다른 사람들이 자신의 컴퓨터에서 작업을 확인할 수 있기를 바란다. 우리는 오류의 원인을 제거하기 위해 다른 연구자가 생성한 에이전트가 동일하기를 원하므로 알고리즘, 아키텍처, 사용된 하이퍼 파라미터 및 때로는 임의의 알고리즘에 대해 가능한 한 상세하게 제공해 주는 것이 중요하다. 우리가 사용한 시드에 대해서도 제공해서 다른 연구자가 생성된 특정 난수 세트를 가지고 알고리즘을 개발하기를 바란다. 이제 ES 문제의 스케일링으로 돌아갑시다. 각 작업자 노드가 처음에 같은 숫자의 시드를 뿌린 경우 교차 및 변경 단계는 정확히 동일하며 각 작업자에서 생성 된 각 세대는 서로 동일 하게 될 것이다. 이것이 바로 우리가 달성하고자하는 것이다. 다음으로 해야 할 일은 적합성을 평가할 에이전트의 부분 집합을 파악하는 것이다. 이 번호를 마스터 노드로 다시 보내고 이 프로세스를 다시 반복 할 수 있다. 우리는 각 작업자 노드가 세대의 에이전트가 평가할 서로에게 통신하도록 할 수 있다.

그런데 작업자 노드들 사이에서도 의사 소통이 필요할까? 각 노드가 항상 동일한 에이전트 부분 집합의 적합성을 평가하도록 구성 할 수 있다. Figure 6.15에서 우리는 각 작업자 노드에 4개 크기의 에이전트 생성이 있음을 보여준다. 첫 번째 노드는 항상 인덱스 0에서 에이전트의 적합성을 평가하고, 두 번째 노드는 인덱스 1에서 에이전트를 담당한다.

6.4.7 선형 확장(Scaling linearly)

위에서 보여준 이 접근 방식은 OpenAI의 연구원들이 수행한 실제 아키텍처의 단순화된 버전이다. 이미 알고 있겠지만, 마스터 노드에게 그렇게 많은 책임이 있어 보이지는 않았지만, OpenAI 엔지니어는 마스터 노드를 아키텍처에서 제거하고 작업자 노드가 서로 직접 통신하도록 했다. 작업자 노드는 지정된 에이전트의 적합성을 계산한 다음 적합성 스칼라 값을 다른 모든 작업자 노드에게 보낸다. 에피소드가 끝날 때, 각 작업자 노드는 세대에 대한 모든 세부 사항을 가지게 될 것이며, 번식(breeding)해야 할 것을 결정할 수 있으며, 그 부분 집합을 교차(Cross, 짝짓기)하고 이 과정을 다시 반복한다. 노드간에 전송되는 데이터의 양을 줄임으로써 추가 노드를 추가해도 전체 네트워크에 큰 영향을 미치지 않았으며 수천개의 작업자 노드로 선형 확장 할 수 있었다.

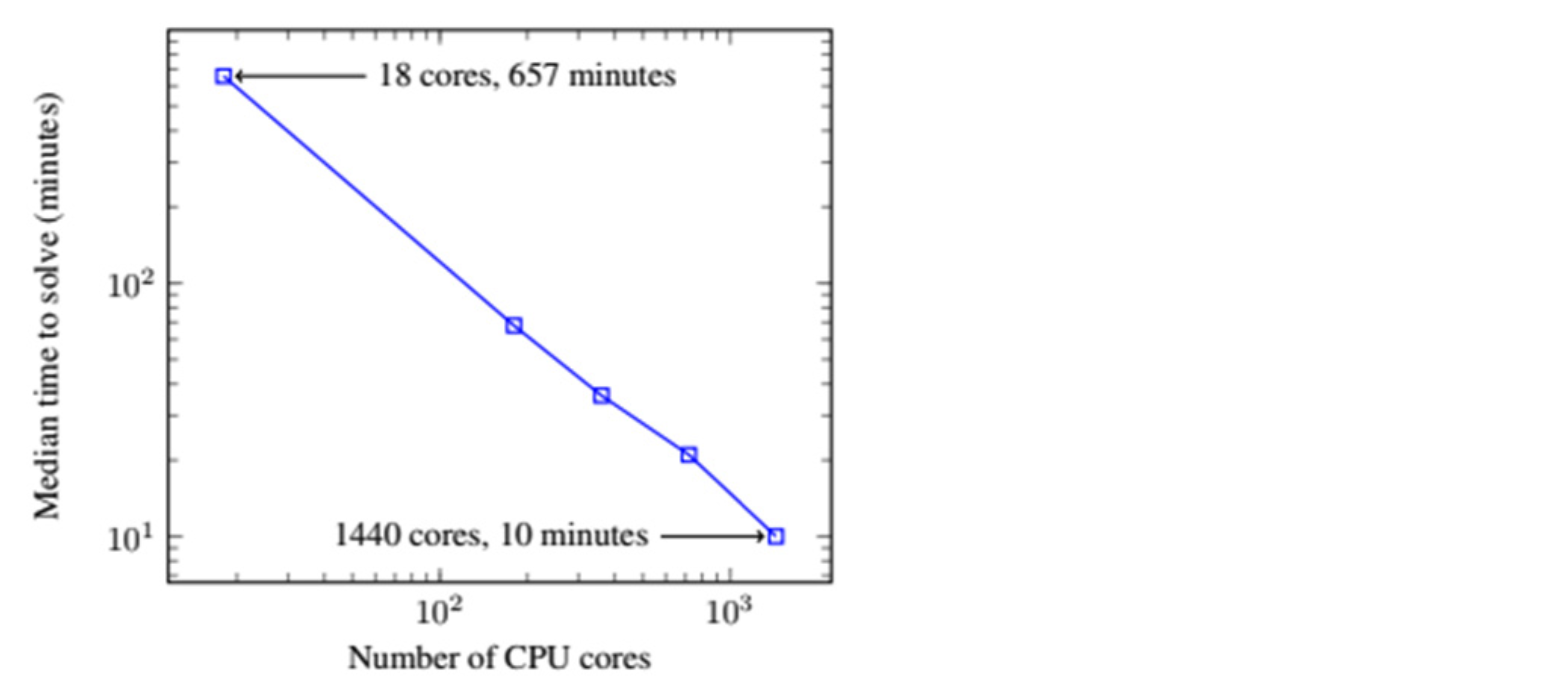
Figure 6.17. 강화 학습에 대한 확장 가능한 대안으로 OpenAI 진화 전략에서 발췌한 그림. 이 그림은 더 많은 컴퓨팅 리소스가 추가됨에 따라 시간 개선이 일정하게 유지되었음을 보여준다.

선형 확장(Scaling linearly)은 머신을 새로 추가한 후와 추가하기 전과 비교했을 때 거의 동일한 성능 향상을 얻음을 의미한다. 이는 Figure 6.17 에서 볼 수 있듯이 자원 대비 성능 그래프에서 직선으로 표시된다.

6.4.8 그라디언트 기반 접근법 확장(Scaling Gradient Based Approaches)

그라디언트 기반 접근 방식은 다수의 컴퓨터에서도 학습 될 수 있다. 그러나 ES만큼 확장 할 수는 없다. 현재, 그라디언트 기반 접근법의 분산 학습을 위한 대부분의 접근법은 각 작업자 노드에 대해 에이전트를 학습시킨 다음 그라디언트를 다시 중앙 시스템으로 전달하여 집계한다. 모든 그라디언트는 각 Epoch 또는 업데이트 주기마다 전달되어야하므로 단일 중앙 시스템에서 많은 네트워크 대역폭과 부담이 필요하다. 결국 네트워크는 포화 상태가 되고 더 많은 작업자 노드를 추가해도 학습 속도가 향상되지 않는다.

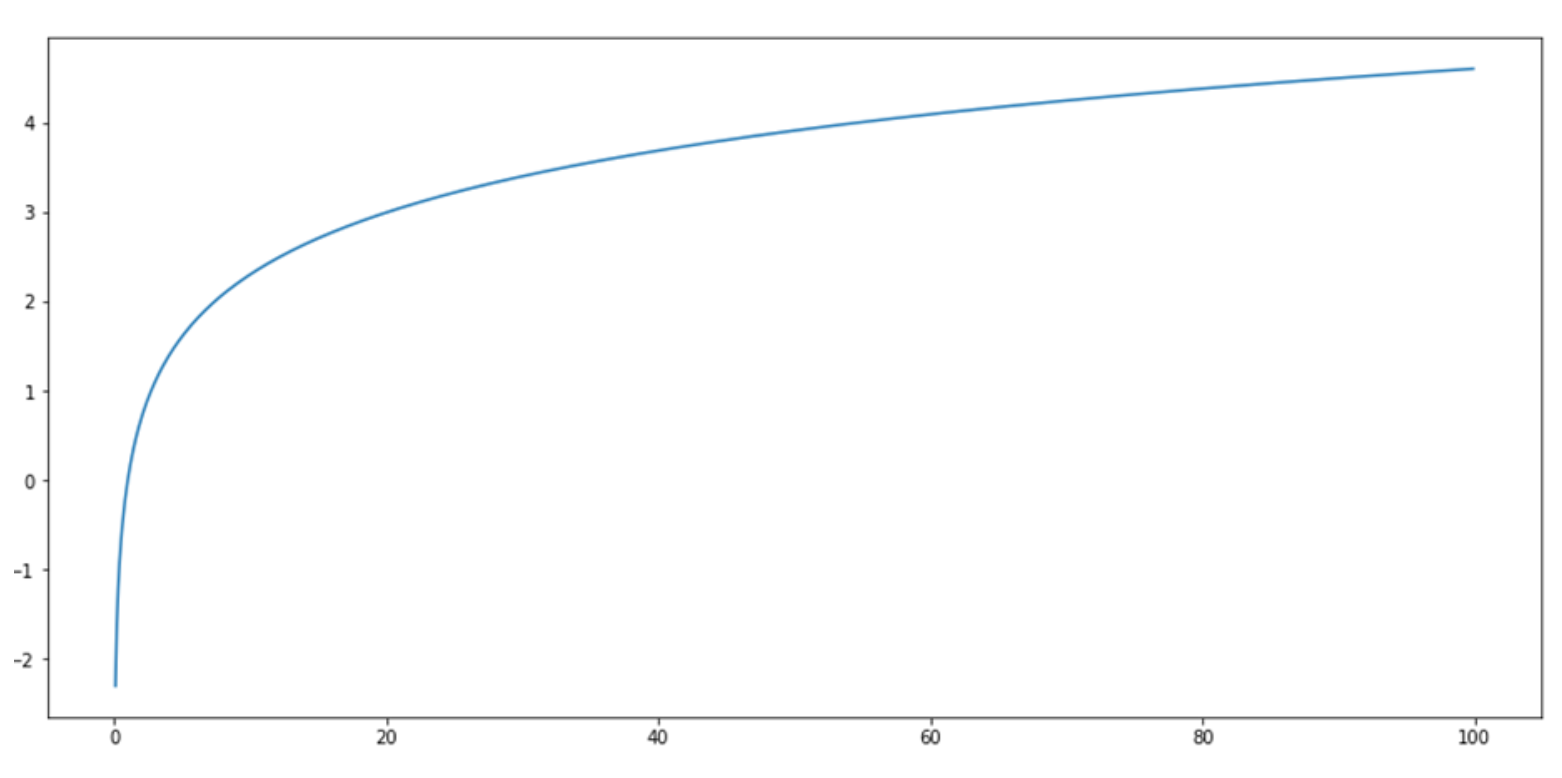
Figure 6.18. 현재 그래디언트 기반 접근 방식의 성능은 이와 같은 그래프와 유사하다. 처음에는 네트워크가 포화되지 않았기 때문에 선형 추세를 따르는 듯 보인다. 그러나 더 많은 리소스가 추가 되어도 성능이 향상되지 않는다.

반면에 진화론적 접근 방식은 역전파가 필요하지 않기 때문에 그라디언트 업데이트를 중앙 서버에 보낼 필요가 없다. 또한 OpenAI가 개발한 것과 같은 똑똑한 기술을 사용하면 단일 숫자만 보내면 된다.

6.5 Summary

• 진화 전략은 강화 학습이라는 무기고에 또 다른 강력한 툴킷을 제공한다.

  우리 인간이 진화한 방식을 적용하기 위해 : 첫째, 개체를 생산한다. 둘째, 현재 세대에서 가장 좋은 것을 선택한다. 셋째, 유전자를 뒤섞는다. 넷째, 변화를 유도하기 위해 돌연변이를 한다. 다섯째, 다음 세대를 위한 새로운 세대를 만들기 위해 짝짓기를 한다.

• 강화 학습 과제에 맞게 진화 알고리즘을 코딩 할 수 있었다. 에이전트의 적합성을 결정하는 방법, 새로운 에이전트를 생성하기 위해 매개 변수를 섞는 방법 및 새로운 변형을 생성하기 위해 돌연변이를 도입하는 방법을 도입해 보았다.
• ES 알고리즘은 그라디언트 기반 접근 방식보다 더 많은 데이터가 사용되고 데이터 효율성이 떨어지는 경향이 있으며, 이는 시뮬레이터가 있는 경우 상황에 따라 문제가 되지 않을 수 있지만 어떤 경우는 시뮬레이터에 접근하지 못할 수 있어(예를 들어 로봇을 학습하려고 하는 경우) 데이터가 매우 부족한 상황으로 인해 문제가 되는 경우이다.
• 다음 장에서는 ES 및 그라디언트 기반 알고리즘보다 데이터 효율성이 더 뛰어난 것으로 알려진 알고리즘들에 대해 설명한다.