DRL Distributioanl DQN
Updated:
Chapter 7. Distributional DQN: Getting the full story
(Orinial Book = ‘Deep Reinforcement Learning in Action’ by Alexander Zai and Brandon Brown)
이 장에서 다룰 내용 :
- 전체 확률 분포를 아는 것이 단일 숫자를 아는 것보다 나은 이유
- Q-values 에 대한 전체 확률 분포를 출력하도록 일반 Deep Q-networks 를 확장하는 방법
- Atari Freeway 게임을 플레이하기 위해 DQN의 분포 변형(distributional variant)을 구현하는 방법
- 일반적인 Bellman 방정식과 분포 변형(distributional variant) 이해하기
- 학습 속도를 향상시키기 위해 Experience Replay의 우선 순위를 정하는 방법
주어진 State에서 가능한 Action을 취할 때의 value(Action-values 또는 Q-values)를 학습하기 위해 3장의 Q-learning 을 다시 소개한다. Q-learning 에서는 Action-values 에 Policy을 적용하여 가장 높은 Action-values 과 연관된 Action를 선택하도록 했었다. 이 장에서는 Q-learning을 확장하여 Action-values의 점 추정(point-estimate)를 배우는 것뿐만 아니라 각 Action에 대한 전체 Action-values 분포를 배운다. 이것을 Distributional Q-learning 이라고 부른다. Distributional Q-learning 은 표준 벤치 마크에서 성능이 크게 향상되는 것으로 나타났으며 앞으로 보게 되겠지만 훨씬 더 미묘한 의사 결정이 가능하다. 이 책에서 다루는 다른 기술과 결합되어 Distributional Q-learning 알고리즘은 현재 강화 학습의 최첨단 기술로 간주되고 있다.
우리가 강화 학습을 적용하려는 대부분의 환경은 어느 정도의 무작위성 또는 예측 불가능성을 포함하며, 주어진 State-Action 쌍에 대해 관찰되는 Reward는 약간의 차이(variance)가 있다. Expected-value Q-learning 이라고 할 수 있는 일반적인 Q-learning 에서는 관찰되는 Reward의 노이즈 집합의 평균만 학습한다. 하지만 평균을 취함으로써 환경의 역학(Dynamics)에 대한 귀중한 정보를 버리게 된다. 경우에 따라 관찰된 Reward는 단일 값을 중심으로 군집되어 있는 것보다 더 복잡한 패턴을 가질 수 있다. 주어진 State-Action 에 대해 서로 다른 Reward 값으로 구성된 두 개 이상의 클러스터가 있을 수 있다. 예를 들어, 동일한 State-Action 에 대해 때로는 Positive Reward가 커지고 때로는 Negative Reward가 커진다. 여기에 평균을 취하면 0에 가까운 값을 얻게 되겠지만 이 경우 실제로 관찰된 Reward가 아니다.
Distributional Q-learning 은 관측된 Reward의 분포를 보다 정확하게 파악하려고 한다. 이를 수행하는 한 가지 방법은 주어진 State-Action 쌍에 대해 관찰된 모든 Reward에 대한 정확한 기록을 유지하는 것이다. 물론 이것은 많은 메모리를 필요로 할 것이고, 높은 차원의 State 공간에 대해서는 계산적으로 비실용적일 것이다. 이런 이유로 우리는 어떤 근사치(approximation)를 만들어야 한다. 먼저, Expected-value Q-learning 이 놓치고 있는 것과 Distributional Q-learning 이 제안하는 것에 대해 자세히 살펴 보겠다.
7.1 Q-learning 에는 어떤 문제점이 있나?
우리가 잘 알고 있는 Q-learning 의 Expected-value 버전에는 결함이 있으며 이를 설명하기 위해 실제 제약 회사 사례를 생각해 본다. 제약 회사가 있고 고혈압(hypertension) 환자가 약물 X라는 새로운 항고혈압 약물 실험의 4주 과정에 어떻게 반응할 것인지를 예측하는 알고리즘을 구축하고 이 알고리즘을 이용해 해당 약물의 처방을 할것인지에 대한 여부를 결정하려고 한다. 우리는 고혈압 환자 집단을 대상으로 치료군(treatment group; 실제 약물을 받을 그룹)과 대조군(control group; 비활성 약물-위약 을 복용하는 그룹)에 무작위 배정된 무작위 임상 시험 (RCT, randomized clinical trial)을 실시하여 다량의 임상 데이터를 수집한다. 그런 다음 각 그룹의 환자가 각각의 약을 복용하는 동안 시간이 지남에 따라 혈압을 기록한다. 결국에는 실제 약물을 복용한 후 반응한 환자가 위약을 복용한 환자 비해 얼마나 나아 졌는지 확인할 수 있다 (Figure 7.1).
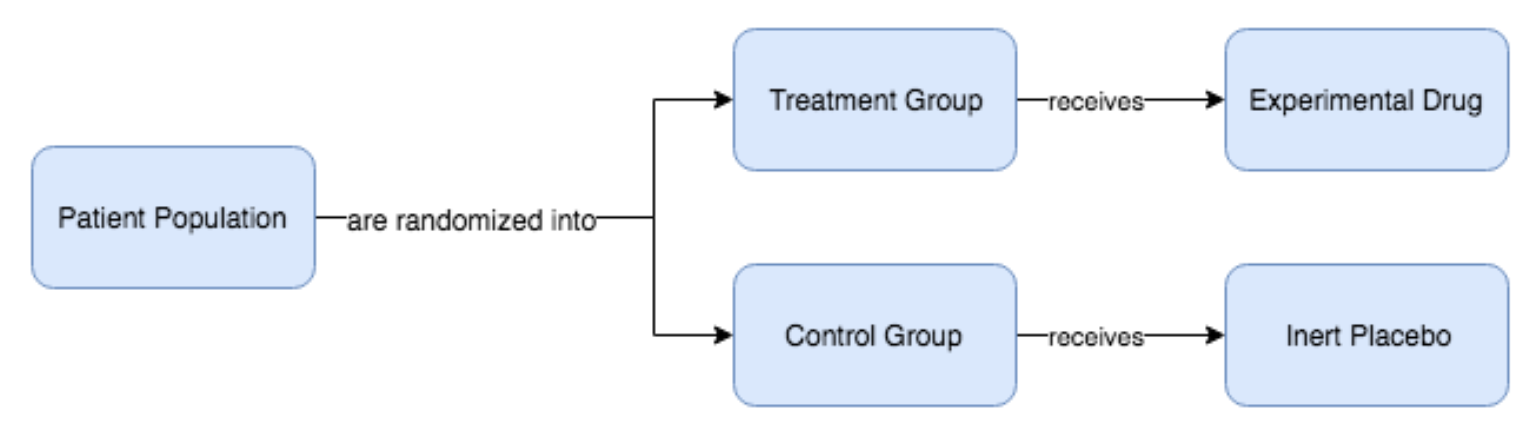
Figure 7.1: 무작위 대조 시험(RCT, randomized control trial)을 통해 위약(비활성 약물)과 비교하여 해당 약물의 치료 효과를 연구한다. 치료 효과를 분리하기 원하므로 어떤 조건을 가진 모집단을 무작위로 두 그룹(치료군과 대조군)으로 나눈다. 치료군은 우리가 시험하고자 하는 실험 약물을 받고, 대조군은 위약을 받는다. 일정 시간이 지나면 두 환자 그룹 모두에 대해 결과를 측정하고 치료군이 평균적으로 위약군보다 더 나은 반응을 보였는지 확인할 수 있다.
이제 데이터셋을 수집했으며 4주 후 치료군 및 대조군의 약물에 대한 혈압 변화의 히스토그램을 시각화할 수 있다. Figure 7.2와 같은 결과가 있다고 가정해 보자.
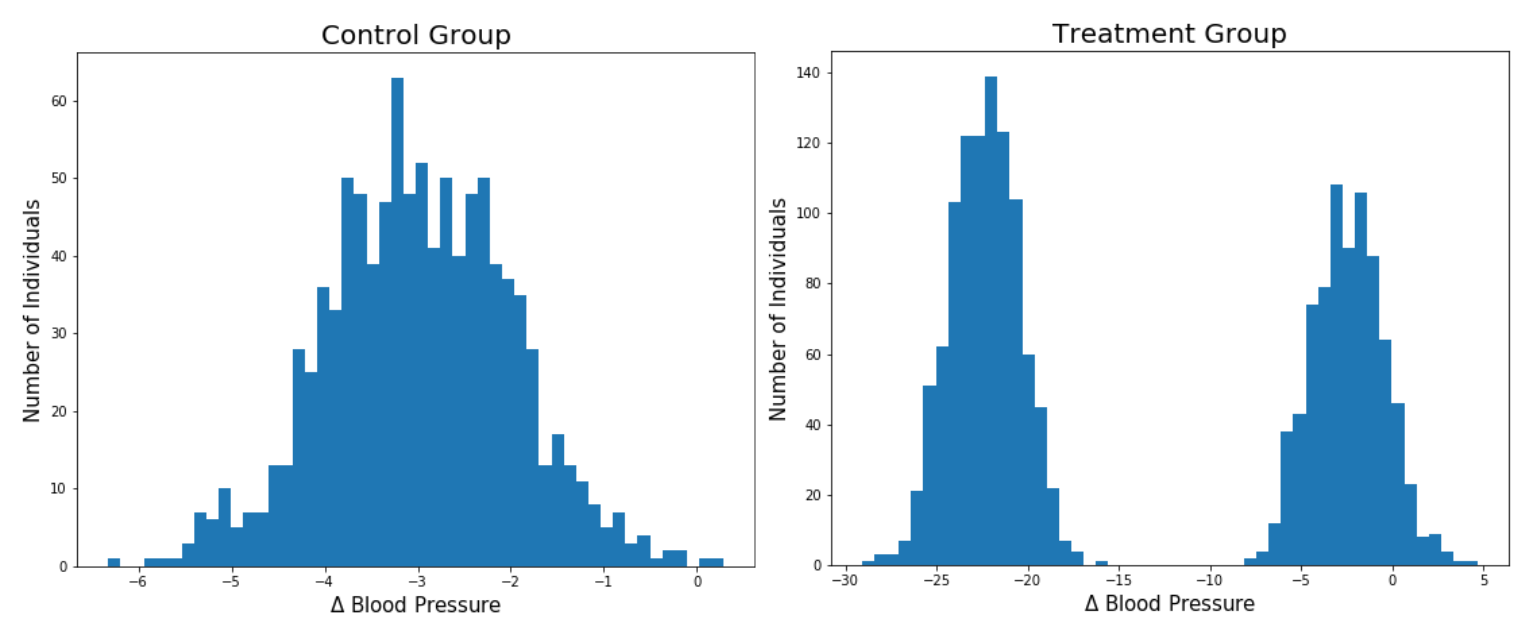
Figure 7.2: 무작위 대조 시험에서 대조군과 치료군에 대한 측정 혈압 변화에 대한 히스토그램이다. x 축은 치료 시작 전부터 치료 후까지의 혈압 변화이다. 우리는 혈압을 낮추기를 원하므로 음수가 좋다. 각 혈압 변화값을 가진 환자의 수를 세기 때문에 -3 근처 가장 높은 부분은 대부분의 환자가 대조군에서 혈압이 3mmHg 감소했음을 의미한다. 치료군에는 두 그룹의 환자가 있는데, 한 그룹은 혈압이 상당히 감소한 그룹이고, 다른 그룹은 최소의 효과를 보거나 효과가 없는 그룹이라고 볼 수 있다. 우리는 이것을 쌍봉분포(bi-modal distribution) 라고 하며, 여기서 모드(mode, 최빈값)는 분포에서 “피크(peak)”의 또 다른 단어이다.
Figure 7.2에 대한 대조군 히스토그램을 먼저 살펴보면, -3.0mmHg(압력 단위)를 중심으로 하는 정규 분포와 비슷해 보이며, 이는 위약을 투여함으로 자연스럽게 기대되는 사소한 혈압 감소로 보여진다. 따라서 우리 알고리즘은 위약을 투여한 환자의 평균 혈압 변화율이 평균 -3.0 mmHg가 될 것으로 예상하지만, 개별 환자의 경우보다 큰 변화가 있더라도 모든 위약 환자의 혈압 변화가 평균 -3.0 mmHg임을 예측할 수 있다. 이제 치료군의 히스토그램을 보자. 혈압 변화의 분포가 쌍봉분포라는 것을 알 수 있다. 이는 두 개의 개별 정규 분포를 합한 것처럼 두 개의 피크가 있음을 의미한다. 가장 오른쪽 모드(mode, 최빈값)는 -2.5 mmHg에 중심을 두고 있으며, 대조군과 매우 유사하며, 치료군 안에 있는 이 서브 그룹은 위약 투여한 환자와 비교하여 약물의 이점이 없음을 시사한다. 그러나 가장 왼쪽에 있는 모드는 -22.3 mmHg에 중심을 두고 있으며, 이는 현재 존재하는 모든 고혈압 치료제보다 훨씬 큰 혈압 감소이다. 따라서 이것은 다시 치료군 내에 서브 그룹이 있음을 나타내며, 이 서브 그룹은 약물의 효과를 많이 보았다. 만약 당신이 의사라고 한다면, 고혈압 환자에게 이 신약을 처방해야 할까? 치료군 분포의 예측값(즉, 평균)을 취하면 약 -13 mmHg의 혈압 변화만 발생하며, 이는 분포의 두 모드(최빈값) 사이의 중간값이다. 이 수치는 여전히 위약을 투여한 환자에 비해 의미가 있지만 시장에 나와 있는 기존의 많은 고혈압 치료제 보다는 성능이 낮습니다. 약물의 혈압 변화에 대한 예측값을 사용하여 결정을 내리는 경우, 많은 환자에게 상당한 효과가 있다는 사실에도 불구하고 이 새로운 약물은 효과가 없는 것으로 보인다. 더욱이, -13 mmHg의 기대값(평균)은 분포를 매우 잘 나타내지 못하는데, 그 이유는 극소수의 환자만이 실제로 그러한 수준의 혈압 감소를 가졌기 때문이다. 환자들은 약물에 대한 반응이 거의 없거나 매우 강력한 반응을 보였고, 중등도의 반응이 있는 환자는 거의 없었다.
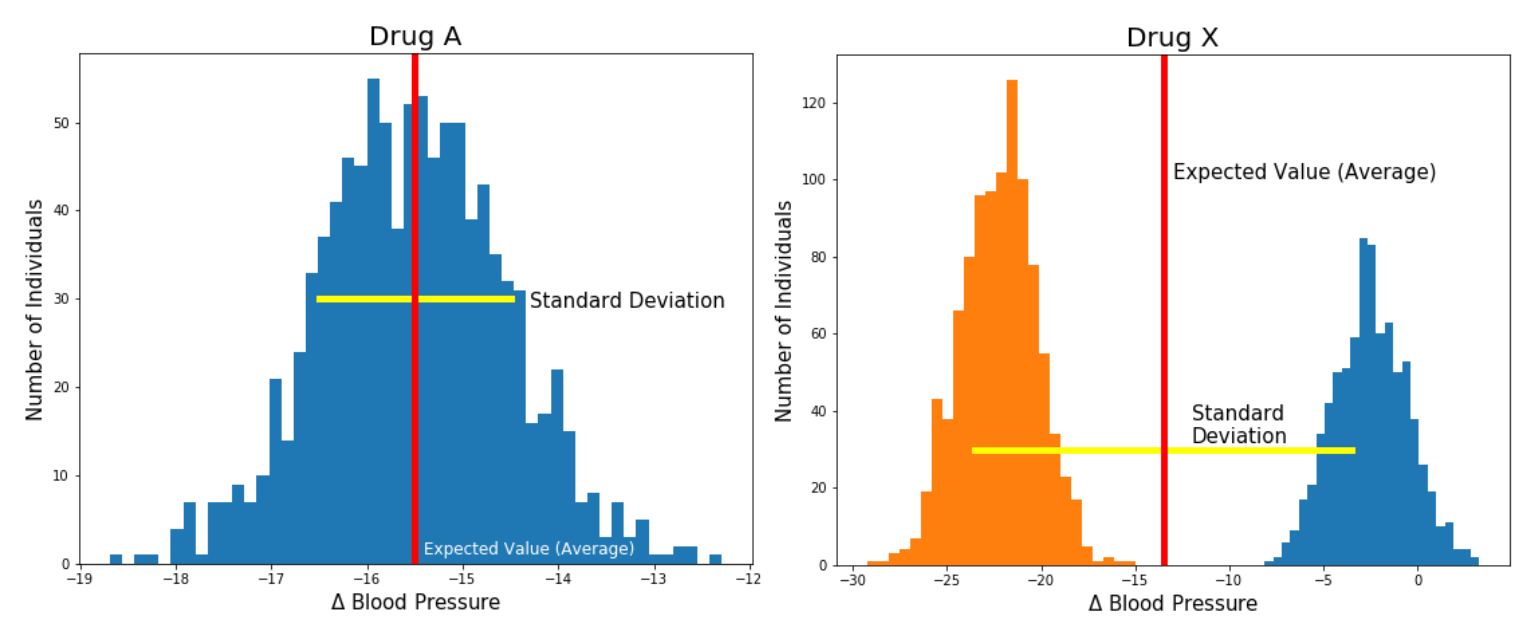
Figure 7.3: 시뮬레이션으로 어떤 약물이 혈압을 가장 많이 낮추는 지 알아보기 위해 약물 A와 약물 X를 실험하여 비교한다 . 약물 A의 평균(예측)값이 -15.5mmHg로 낮고 표준 편차가 더 낮지만 약물 X는 -22.5mmHg를 중심으로하는 모드를 가진 쌍봉분포입니다. 약물 X의 경우, 평균 수치에 가까운 혈압 변화있는 환자가 거의 없다.
위 예는 전체 분포를 보는 것과 비교되는 예측값의 한계를 보여 준다. 모집단 수준에서 각 약물에 대한 혈압 분포의 예측값을 사용하여 혈압 변화 측면에서 예측값이 가장 낮은 약물을 선택한다면 (부작용과 같은 환자의 특정 복잡도는 무시) 모집단 수준에서는 최적으로 행동한다. 보다 구체적으로, 약물 A, 약물 B 및 약물 C의 평균 혈압 변화가 -5.1 mmHg, -15.2 mmHg 및 -9.5 mmHg 인 경우, 약물 B가 가장 큰 영향을 미치기 때문에 항상 B로 처방하여 모집단 수준에서는 평균적으로 최적으로 행동할 것이다. 물론, 의사는 여러 가지 복잡한 이유로 실제로 이렇게 행동하지는 않지만, 멀티모달(multi-modality)로 의약품을 처방 할 때 기대값(평균)을 사용하지 않는 한 가지 이유는 멀티모달(multi-modality)로 인해 위험을 다르게 평가할 수 있기 때문이다. 가상의 약물 X를 싱글 모드(single mode)로, 약물 A를 두가지 모드(two mode)를 가진 것으로 비교한 Figure 7.2를 생각해 본다. 약물 X가 환자의 혈압을 -22.3 mmHg 감소시킬 가능성도 있고 감소할 가능성이 없기도 한 경우, 약물 비용을 지불해야 하는 의료 시스템(또는 환자)은 약물 X를 처방하는 것 원하지 않을 수 있다. 중간 정도의 단일 효과를 가진 약물을 선택하는 것과는 반대로 어떤 환자에 대해서는 전혀 효과를 보지 못하는 약물을 구입하는 것의 리스크를 떠안지 않는 것이 덜 위험하기 때문이다. 전체 분포가 중요한 또 다른 이유는 환자가 특정 혈압 목표치를 가질 수 있기 때문이다. 예를 들어, 고혈압이 심한 환자는 혈압을 20mmHg 이상 줄여야 할 수 있습니다. 약물 X가 효과가 있다면, 하나의 약물만 사용하면 된다. 약물 X가 없으면 여러 가지 다른 약물을 복용해야 한다. 따라서 약물 X의 예측값이 -9 mmHg 인 경우 약물 X에 반응이 강한 환자의 유형인 경우 환자에게 필요한 유일한 약물 일 수 있다는 사실을 놓치게 된다.
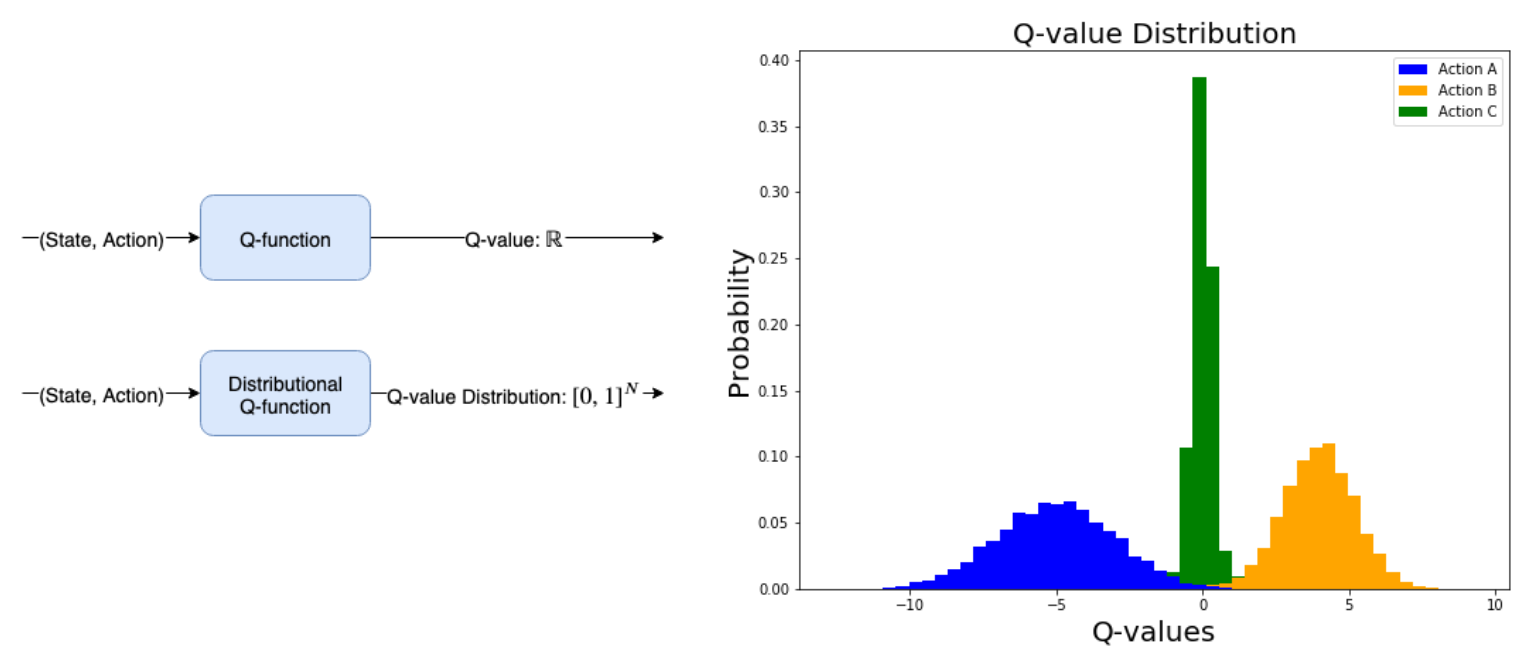
Figure 7.4 : 왼쪽 위 : 일반적인 Q-function 은 State-Action 쌍을 가져와 관련 Q-values 을 계산한다. 왼쪽 아래 : Distributional Q-function 은 State-Action 쌍을 취하고 가능한 모든 Q-values 에 대한 확률 분포를 계산한다. 확률은 [0,1]사이의 값으로 제한되므로 [0,1] 사이 값을 가진 모든 요소가 포함된 벡터를 반환하고 합계는 1이다. Action A는 평균 Reward -5로, 반면 Action B는 평균 Reward +4 이다.
이것이 심층 강화 학습과 어떤 관련이 있을까? 우리가 배운 Q-learning 은 우리에게 예상되는 (average, time-discounted) State-Action 값을 제공하며, 이것이 다봉분포(multi-modal distribution) 약물의 경우에 대해 논의했던 것과 동일한 제한을 초래할 수 있다고 생각할 수 있다. State-Action 값에 대한 전체 확률 분포를 학습하는 것은 일반적인 Q-learning 의 예측값을 학습하는 것보다 훨씬 많은 장점이 있다. 전체 분포를 사용하면 State-Action 값에 멀티모달(multi-modality)이 있는지 여부와 분포에 분산(variance)이 얼마나 있는지 확인할 수 있다. 세 가지 다른 Action에 대한 Action-values 분포를 모델링 한 Figure 7.4를 보면 일부 Action이 다른 Action과 차이가 있음을 알 수 있다. 이 추가 정보를 통해 위험에 민감한 Policy, 즉 Expected Reward를 극대화 할뿐만 아니라 그렇게 하는 데 따르는 위험의 양을 통제하는 Policy를 사용할 수 있다.
현재까지 가장 설득력있는 연구는, 몇 가지 인기있는 DQN variant와 DQN의 Distributional variant을 포함하여 원래의 DQN 알고리즘에 대한 개선을 평가한 경험적 연구 (“Rainbow: Combining Improvements in Deep Reinforcement Learning” by Hessel et al 2017)이고 Rainbow는 그 동안의 DQN 계열의 연구들중 현재까지 가장 효과적이었고 중요한 연구들을 결합하여 합친 연구이다. Distributional Q-learning 은 Rainbow에서 테스트한 DQN에 대한 모든 개별 개선 중에서 전체적으로 가장 우수한 알고리즘이라는 것이 밝혀졌다. DQN 관련 모든 기술을 “Rainbow” DQN으로 결합하여 어떤 DQN의 개별 기술보다 훨씬 효과적인 것으로 나타났다. Rainbow의 성공에 가장 중요한 구성 요소가 무엇인지 확인했는데 Distributional Q-learning , Multi-step Q-learning (5 장 참조) 및 Prioritized Replay(이 장에서 간략히 설명)이 Rainbow 알고리즘의 성능에 가장 중요한 영향을 미쳤다.
이 장에서는 State가 주어진 각 가능한 Action에 대한 State-Action 값에 대한 확률 분포를 출력하는 Dist-DQN (Distributed Deep Q-Network)을 구현하는 방법을 공부한다. Policy Gradient 장에서 일부 신경망 네트워크를 Action에 대한 확률 분포를 직접 출력하는 Policy function 으로 사용하는 몇 가지 확률 개념을 보았지만 이러한 개념을 다시 검토하고 이해하는 것이 중요하므로 더 깊이 들어가 알아보겠다. Dist-DQN을 구현할 때 너무 학문적으로 보일지 모르지만 실제 구현시에 확률적 개념의 학문적 이론적 이해가 왜 필요한지 분명해질 것이다. 이 장은 처음에는 이해하기 어려운 상당한 양의 확률 개념을 포함하므로 이 책 전체에서 가장 개념적으로 어려운 장이다. 다른 장보다 더 많은 수학이 있다. 이 장을 통해 큰 성과를 거둘 수 있으며 머신 러닝 및 강화 학습에서 매우 중요한 주제를 많이 배우거나 검토하여 이 분야에 대해 더 잘 이해할 수 있다.
7.2 확률과 통계 다시보기
확률 이론 배후에 있는 수학은 일관되고 논쟁의 여지가 없지만, “동전던지기에서 공정한 동전을 사용할 때 앞면이 나올 확률이 0.5 이다.” 와 같이 사소한 의미도 그 의미의 해석은 실제로 다소 논쟁의 여지가 있다. 확률에 대한 해석을 달리하는 두 가지의 진영이 있는데 빈도주의자(Frequentist) 와 베이지안(Bayesian) 이다. 빈도주의자는 동전이 앞면이 나올 확률은 동전을 무한번 던질 때 앞면이 나올 비율이라고 말합니다. 동전던지기에서 초기에는 앞면이 나올 확률이 0.8의 높은 비율로 나타날 수 있지만, 동전던지기를 계속해서 무한적으로 진행하면 정확히 확률이 0.5를 향하는 경향이 있다. 그래서 빈도주의자들은 확률은 사건의 빈도 일뿐이라고 말한다. 이 경우 두 가지 가능한 결과, 동전의 앞면과 뒷면이 있으며 각 결과의 확률은 무한한 횟수의 시도 (동전던지기) 후의 빈도이다. 이것은 물론 확률이 0(Impossible)에서 1(Certain) 사이의 값이고 가능한 모든 결과들에 대한 합이 1 이어야 하는 이유이다.
이와 같은 해석은 확률에 대한 간단하고 직접적인 접근 방법이지만 중대한 한계가 있다. 빈도주의로 해석할 때 “제인 도(Jane Doe)가 시의회에 선출될 확률은 얼마인가?”와 같은 질문은 답을 내기 어렵거나 불가능하다. 선거는 무한한 횟수로 일어나는 것이 아니기 때문에 이 문제를 빈도주의 관점에서 이해하는 것은 실제적으로나 이론적으로나 불가능하다. 이러한 일회성 사건에는 빈도주의적 확률이 의미가 없다. 이러한 상황을 처리 할 수 있는 보다 강력한 프레임워크가 필요하고 베이지안 확률이 그것이다.
베이지안으로 해석할 때 확률은 다양한 가능한 결과에 대한 신뢰도(Degree of Belief)을 나타낸다. 이 경우는 선거와 같이 한 번만 일어날 수 있는 일에 대한 신뢰도를 가질 수 있으며, 일어날 수 있는 일에 대한 신뢰도는 특정 상황에 대한 정보의 양과 새로운 정보로 인해 신뢰도를 업데이트하게 할 수 있는 가에 따라 달라질 수 있다. (Table 7.1).
Table 7.1: Frequentist versus Bayesian Probabilities
어쨌든 기본 수학 프레임워크는 특정 질문에 대해 가능한 모든 결과 집합인 표본 공간(Sample Space) Ω으로 구성된다. 선거의 경우 표본 공간은 선거에서 이길 수 있는 모든 후보자의 집합이다. 그런 다음 확률 분포 (또는 측정) 함수 P : Ω → [0,1]이 있습니다. 즉 P는 표본 공간에서 0에서 1사이의 실수에 대한 함수이다. 따라서 P(후보 A) 는 후보 A가 선거에서 이길 확률을 나타내는 0에서 1사이의 숫자를 리턴한다.
확률 이론(Probability Theory) 참고: 기술적으로 확률 이론은 여기에 설명된 것보다 더 복잡하며 측정 이론(measure) 이라고 하는 수학이 포함된다. 우리의 목적을 생각한다면 확률 이론에 대해 더 깊이 탐구할 필요가 없고 앞으로 필요로 하는 확률 개념에 대해 비공식적이고 수학적으로 비엄격하게 소개하겠다.
우리가 사용할 또 다른 용어는 확률 분포의 서포트(Support)이다. 서포트는 0이 아닌 확률이 할당된 결과의 하위 집합일 뿐이다. 예를 들어 온도는 0 Kelvin 보다 작을 수 없으므로 음의 온도에는 확률 0이 지정되므로 온도에 대한 확률 분포의 서포트는 0에서 양의 무한대에 불과하다. 일반적으로 불가능한 결과에 대해서는 신경 쓰지 않기 때문에 서포트 또는 표본 공간이 동일하지 않더라도 호환 가능하게 사용되는 경우가 종종 있다.
7.2.1 사전확률과 사후확률(Priors and Posteriors)
“4-way 레이스에서 우승할 각 후보의 확률은 얼마입니까?” 후보자가 누구인지 또는 선거에 관한 내용을 명시하지 않고는 정보가 충분하지 않다고 대답하기를 거부 할 수도 있다. 계속 답변을 요구하고 추가적인 정보가 없다면, 당신은 각 후보자가 1/4의 확률로 승리할 것이라고 답변할 것이다. 이 답변을 통해 후보자에 대해 균일한(각 가능한 결과는 동일한 확률을 가짐) 사전 확률 분포(Prior Probability Distribution)을 설정한 것이다. 베이지안 프레임워크에서 확률은 신뢰도을 나타내며 새로운 정보를 이용할 수 있는 상황에서는 신뢰도가 항상 잠정적이므로 사전 확률 분포는 새로운 정보를 받기 전에 시작하는 분포일 뿐이다. 후보자에 대한 이력 정보와 같은 일부 새로운 정보를 수신 한 후 새로운 정보를 기반으로 이전 분포를 업데이트 할 수 있으며 이 업데이트 된 분포를 이제 사후 확률 분포(Posterior Probability Distribution) 라고 한다. 그러나 사후 확률 분포는 다른 일련의 새로운 정보를 받기 직전에 새로운 사전 확률 분포가 되기 때문에 사전 분포와 사후 분포의 구별은 전후사정에 따른다. 신뢰도는 사전 분포에서 사후 분포로의 연속됨에 따라 지속적으로 업데이트 된다 (Figure 7.5).
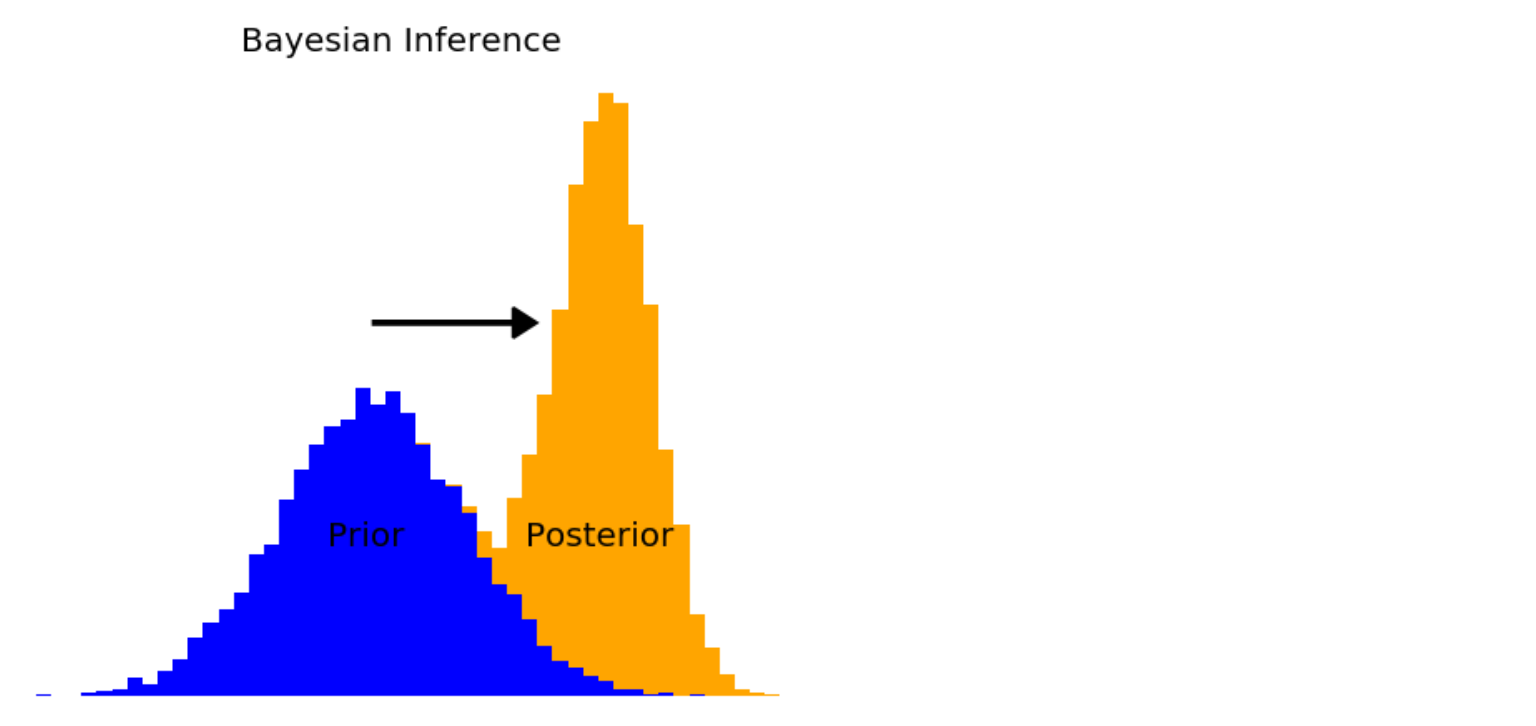
Figure 7.5 : 베이지안 추론은 사전 분포로 시작하여 새로운 정보를 수신하고,이를 이용하여 사전 분포를 사후 분포라고 하는 새롭고 보다 정보가 추가된 분포로 업데이트하는 프로세스이다.
7.2.2 기대값과 분산(Expectation and Variance)
확률 분포와 관련하여 여러 가지 질문이 있을 수 있다. “가장 가능성이 높은” 표본이 무엇인지 질문할 수 있는데, 이는 일반적으로 분포의 평균(Mean 또는 Average) 이다. 모든 표본의 합계를 표본 수로 나누는 평균을 계산하는 방법에 아마도 이미 익숙 할 것이다. 예를 들어 [18,21,17,17,21] ° C 5일간 예보한 기온의 평균은 ([18 + 21 + 17 + 17 + 21]) / 5 = 94 / 5 = 18.8 ° C 입니다. 해석하면 미국 일리노이주 시카고에서 5일 동안의 평균 예측 기온입니다.
5명의 사람들에게 시카고의 내일 기온에 대한 예측을 해달라고 요청했고 [18,21,17,17,21] ° C와 같은 숫자를 주었다고 생각해 봅시다. 내일의 평균 기온를 원한다면 동일한 절차를 수행하여 주어진 숫자를 모두 더한 후 전체 표본 수(5)로 나눠서 내일의 평균 예측 기온을 구한다. 그러나 만약 사람 1이 기상학자이고 우리가 거리에서 무작위로 조사한 다른 4 명에 비해 기상학자의 예측에 대해 더 많은 확신을 가지고 있다면 어떨까? 우리는 아마도 기상학자의 예측을 다른 것보다 더 높이 평가하고 싶을 것이다. 기상학자의 예측이 60%가 맞을 가능성이 있고 다른 4명이 참일 가능성이 10%에 불과하다고 가정하면 ( 1 * 0.6 + 4 * 0.1 = 1.0), 이는 가중 평균(weighted average)이며 각 값을 곱하여 계산된다. 이 경우 [(0.6 * 18) + 0.1 * (21 + 17 + 17 + 21)] = 18.4 ° C 이다. 주어진 각 표본의 값은 내일의 온도를 나타낼 수 있지만 이 경우 모든 표본이 동일한 가능성을 가지고 있는 것은 아니므로 가능한 모든 표본에 확률(Weight)을 곱한 다음 더한다. 모든 가중치(Weight)가 같고 합계가 1이면 평균이다. 실세계의 문제는 많은 경우 평균을 구하는 문제보다 가중 평균을 구하는 경우가 많다. 평균보다 더 일반적인 가중 평균을 분포의 기대값(Expectation Value)이라고 한다. 확률 분포의 기대값은 평균일 가능성이 가장 높은 값인 해당 분포의 “무게 중심(center of mass)” 이다. x가 표본 공간인 확률 분포 P(x)가 주어지면 이산 분포(Discrete Distribution)에 대한 기대값은 Table 7.2와 같이 계산된다.
Table 7.2: 확률 분포로 부터 기대값 구하기
Math
𝔼[P]=∑x⋅P(x)
Python
>>> x = np.array([1,2,3,4,5,6])
>>> p = np.array([0.1,0.1,0.1,0.1,0.2,0.4])
>>> def expected_value(x,p):
>>> return x @ p
>>> expected_value(x,p) 4.4
기대값 연산자는 𝔼로 표시되며 확률 분포를 사용하여 기대값을 반환하는 함수이다. 값 x를 취하고 관련 확률 P(x)를 곱하여 합하면 됩니다. 위의 파이썬 코드에서 P(x)는 numpy 배열인 probs 로 각 표본이 나타날 확률을 나타내고, 다른 numpy 배열인 outcomes 는 표본 공간을 나타낸다. 이때 기대값은 18.4이다.
>>> import numpy as np
>>> probs = np.array([0.6, 0.1, 0.1, 0.1, 0.1])
>>> outcomes = np.array([18, 21, 17, 17, 21])
>>> expected_value = 0.0
>>> for i in range(probs.shape[0]):
>>> expected_value += probs[i] * outcomes[i]
>>> expected_value
18.4
또는 기대값은 probs 배열과 outcomes 배열 사이의 내적(inner product, dot product)으로 계산 될 수 있다. 내적은 위 코드와 동일한 작업을 수행하므로 두 배열의 각 해당 요소를 곱하고 모두 합한다.
>>> expected value = probs @ outcomes
>>> expected_value
18.4
이산 확률 분포(Discrete Probability Distribution)는 표본 공간(Sample Space)이 유한 집한(Finite Set)이다. 즉, 한정된 수의 표본만 발생할 수 있음을 의미한다. 동전던지기는 두 가지 결과 중 하나 일 수 있지만, 내일 기온 예측하기는 임의의 실수(켈빈 단위로 측정 한 경우 0에서 무한대까지의 숫자 일 수 있음)일 수 있으며 실수 또는 실수의 일부는 무한대이다. 실수는 계속해서 나눌 수 있기 때문에, 예를 들어 1.5는 실수이고 1.500001 도 실수이다.
표본 공간이 무한하면 연속 확률 분포(Continuous Probalility Distribution) 이다. 이 경우 확률 분포는 특정 표본의 확률을 나타내지 않는다. 합이 1이 되려면 각 개별 표본에 무한히 작은 확률이 있어야 하기 때문이다. 연속 확률 분포는 특정 가능한 사건에 대한 확률 밀도(Probability Density)를 알려준다. 확률 밀도는 작은 간격, 즉 사건이 두 수 사이에 속할 확률의 합이다. 이 책에서 우리는 실제로 이산 확률 분포만 다룰 것이기 때문에 연속 확률 분포에 대해서는 이정도로만 다루도록 하겠다.
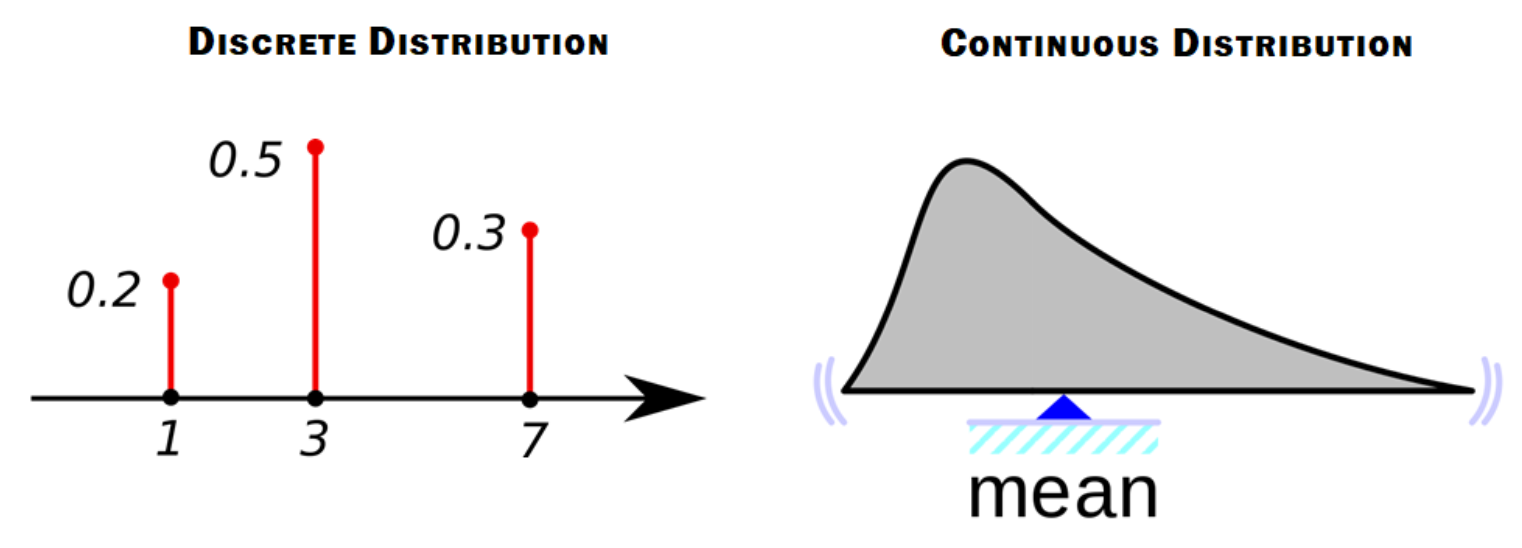
Figure 7.6: 왼쪽 : 이산 분포는 표본과 표본과 연결되어 나올 확률들을 표현한 numpy 배열과 같이 표현된다. 오른쪽 : 연속 분포는 x축은 무한한 가능한 표본를 나타내고 y 축은 확률 밀도를 나타낸다. (확률 밀도는 사건이 두 수 사이의 값을 취할 확률이다.)
확률 분포에 관해 질문 할 수 있는 또 다른 질문은 확률 분포의 퍼짐을 나타내는 분산(Variance) 이다. 무언가에 대한 우리의 신뢰도는 더 많을 수도 더 적을 수도 있으므로 확률 분포는 좁거나 넓을 수 있다. 분산 계산에는 기대값 연산자가 사용되며 Var(X) = σ2 = 𝔼[(X-μ)2] 로 정의되지만 내장된 numpy 함수를 사용하여 계산하므로 이 식을 기억할 필요는 없다. 분산은 Var(X) 또는 σ2(시그마 제곱)로 표시되며, 여기서 √(σ2) = σ 는 표준 편차이므로 분산은 표준 편차 제곱이다. 이 방정식의 μ는 평균에 대한 표준 기호이며 다시 μ = 𝔼[X]이고 여기서 X는 확률 변수(Random Variable)입니다.
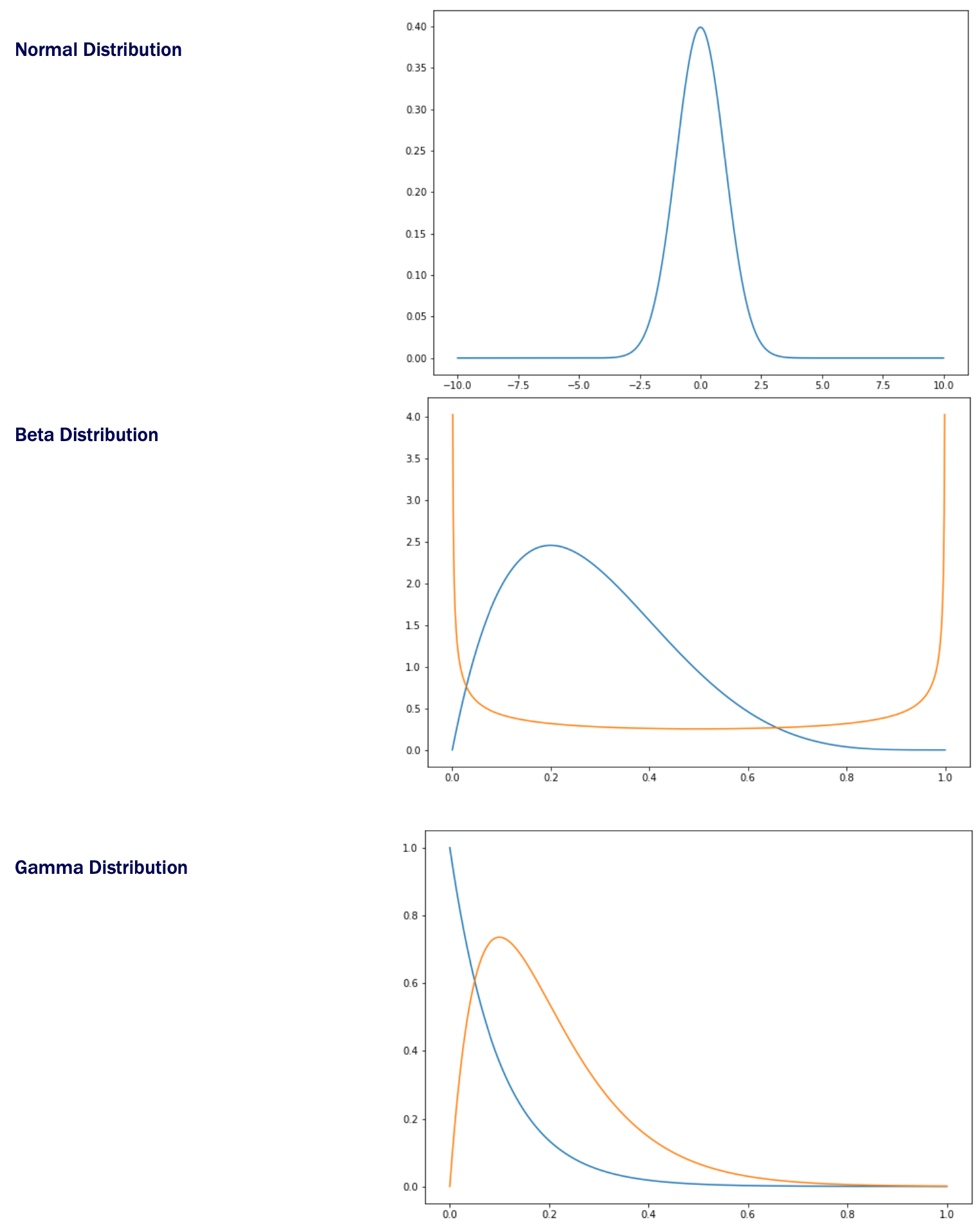
Common Probability Distributions
확률 변수는 일반적으로 X와 같이 대문자로 표시됩니다. 파이썬에서는 numpy의 랜덤 모듈을 사용하여 랜덤 변수를 설정할 수 있습니다.
>>> t0 = 18.4
>>> T = lambda: t0 + np.random.randn(1)
>>> T()
array([18.94571853])
>>> T()
array([18.59060686])
여기서 확률 변수 T는 인수를 허용하지 않고 호출 될 때마다 18.4에 작은 임의의 숫자를 추가하는 익명 함수로 만들었다. 따라서 T의 분산은 1이며, 이는 T가 반환할 가능성이 있는 대부분의 값이 18.4를 중심으로 1 내에 있음을 의미핟다. 분산이 10이면 가능한 온도의 퍼짐이 더 커집니다. 일반적으로 분산이 높은 사전 분포로 시작하여 더 많은 추가 정보를 얻을수록 분산이 감소한다. 그러나 만약 우리가 얻는 추가 정보가 예상할 수 없고 확실하지 않다면 새로운 정보가 사후 분포의 분산을 증가시킬 수 있다.
7.3 벨만 방정식(The Bellman Equation)
1 장에서 Bellman을 언급했지만 여기서는 많은 강화 학습 알고리즘을 뒷받침하는 Bellman 방정식에 대해 배울 것이다. Bellman 방정식은 강화 학습 문헌의 모든 곳에 나타나므로 적어도 섹션을 포함하는 것이 중요하다고 생각했지만, 실제로 Python을 코드를 작성하는 때는 Bellman 방정식을 이해하지 않고도 할 수 있다. 이 섹션은 좀 더 수학적 배경에 관심이 있는 사람들을 위한 옵션이다.
Q-function 은 State-Action 쌍의 값을 알려주며, 값은 time-discounted Reward의 expected sum으로 정의된다. 예를 들어, 그리드 월드 게임에서 Qπ(s, a)는 상태에서 조치를 취하고 그 이후 정책 π를 따르는 경우 얻을 수있는 평균 Reward를 알려 준다. Optimal Q-function은 Q로 표시되며 완벽하게 정확한 Q-function이다. 무작위로 초기화된 Q-funcion 으로 게임을 시작하면 매우 부정확한 Q-value 예측을 받지만 목표는 Q-function이 최적의 Q에 가까워 질 때까지 반복적으로 업데이트하는 것이다. Bellman 방정식은 Reward가 있을 때 Q-function을 업데이트하는 방법을 알려 준다.
Qπ(st, at) ← rt + γ⋅Vπ(st+1), Where Vπ(st+1) = max[Qπ(st+1, a)]
현재 State의 Qπ(st, a)의 Q-value는 관측된 Reward rt와 다음 State Vπ(st + 1)의 값에 Discount Factor γ (← 왼쪽 화살표는 “오른쪽의 값을 왼쪽의 변수에 할당” 을 의미). 다음 State의 값은 단순히 다음 State에 대해 가장 높은 Q-value가 무엇이든간에 가능하다 (가능한 Action마다 다른 Q-value를 얻으므로). 신경망을 사용하여 Q-function을 근사할 때, 신경망의 parameter를 업데이트하여 Bellman 방정식의 왼쪽에 있는 예측된 Qπ(st, at)와 오른쪽에 있는 계산값 사이의 오류를 최소화하려고 한다.
THE DISTRIBUTIONAL BELLMAN EQUATION
Bellman 방정식은 Environment가 결정론적(deterministic)이므로 관측된 Reward도 결정론적(deterministic)이라고 가정한다. 즉, 동일한 State에서 동일한 Action을 취하면 관측된 Reward는 항상 동일하다. 어떤 경우에는 이것이 사실이지만 어떤 경우에는 그렇지 않다. 우리가 사용하고 사용할 모든 게임 (Gridworld 제외)에는 적어도 어느 정도의 무작위성(randomness)이 있다. 경우에 따라 게임의 프레임을 다운 샘플링 할 때 원래 두 가지 상태가 동일하게 매핑되기 때문에 다운 샘플링된 상태로 인해 관측된 Reward에서 예측할 수 없는 결과가 발생한다. 따라서 이 경우 결정론적 변수 rt를 확률 분포를 갖는 확률 변수 R(s, a)로 만들 수 있다. State가 새로운 State로 진화하는 방식에 무작위성이 있는 경우 Q-function도 확률 변수 이어야 한다. 위의 원래 Bellman 방정식은 이제 다음과 같이 나타낼 수 있다.
Q(st,at)← 𝔼[R(st,a)]+γ⋅ 𝔼[Q(st+1, At+1)]
다시 말하지만 Q-function은 확률 변수로, Environment가 확률적 전이(stochastic transition)를 갖는 것으로 해석하기 때문이다. 즉, Action를 취하는 것이 동일한 다음 State로 이어지지 않을 수 있다. 따라서 다음 State와 Action에 대한 확률 분포를 얻는다. 따라서 다음 State-Action 쌍의 예상 Q-value는 다음 State-Action 쌍이있을 가능성이 가장 높은 Q-value이다. 기대값 연산자를 제거하면 전체 Distributional Bellman 방정식을 얻는다.
Z(st,at)←R(st,at)+γ⋅Z(st+1, At+1)
여기서 Z를 사용하여 Distribution Q-value function (Value Distribution 라고도 함)를 나타낸다. 우리가 원래 Bellman 방정식으로 Q-learning 을 할 때, 우리의 Q-function 은 가능한 최선의 Value Distribution의 기대값을 배울 것이다. 그러나 이 장에서 우리는 약간 더 복잡한 신경망을 사용할 것이다. Value Distribution를 통해 실제로 기대값이 아닌 관측된 Reward의 분포를 배울 수 있습니다. 이는 첫 번째 섹션에서 설명한 이유, 즉 분포를 학습함으로써 분포의 분산과 가능한 multi-modality를 고려하여 Risk-sensitive Policy를 활용할 수 있는 방법이 있다는 점에서 유용하다.
7.4 Distributional Q-learning
이제 실제로 distributional deep Q-network (Dist-DQN)를 구현하는 데 필요한 모든 준비 사항을 다뤘다. 이전 섹션의 모든 내용을 완전히 이해하지 못했다해도 걱정하지 않아도 된다. 코드 작성을 시작할 때 더 명확 해질것이다. 이 장에서는 OpenAI Gym, Freeway 가장 간단한 Atari 게임 중 하나를 사용하여 랩탑노트북 CPU에서 알고리즘을 학습 할 수 있다. 다른 장과 달리, 게임의 RAM 버전을 사용할 것이다. https://gym.openai.com/envs/#atari에서 사용 가능한 게임 환경을 살펴보면 각 게임에는 “RAM”이라는 레이블이 지정된 두 가지 버전이 있다.
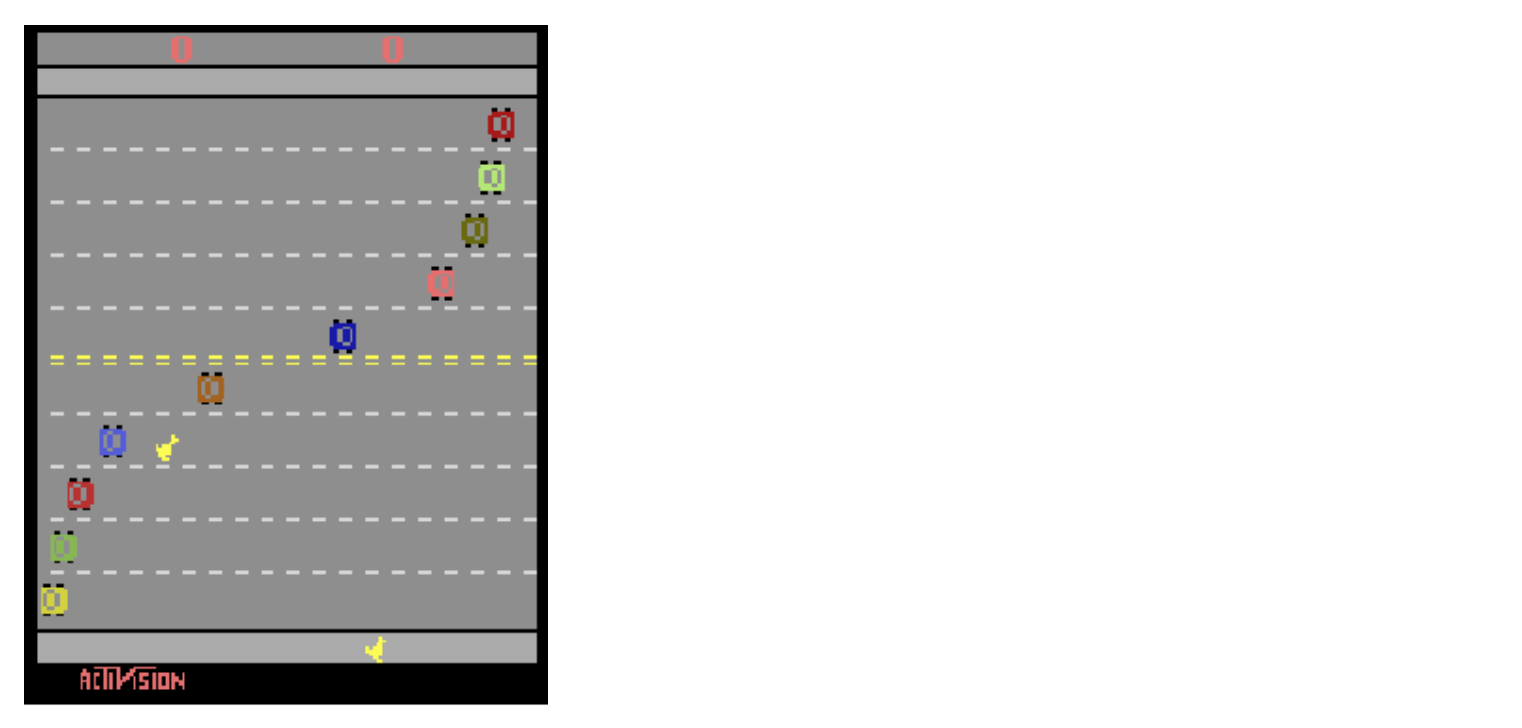
Figure7.8: Atari 게임 Freeway의 스크린 샷. 게임의 목표는 다가오는 자동차를 피하면서 고속도로를 가로 질러 닭을 움직이는 것이다.
Freeway는 UP, DOWN 또는 NOOP ( “no-operation”) Action으로 닭을 제어하는 게임이다. 목표는 다가오는 자동차를 피해서 고속도로를 가로 질러 닭을 움직여 +1의 보상을 받아 반대편에 도착하는 것이다. 제한된 시간 내에 3 마리의 닭을 모두 잃으면 게임에서 지고 Negative Reward를 받는다.
7.4.1 파이썬에서 확률 분포 표현
기존의 일반적인 DQN이 단일 Q-value를 반환하는 Q-function Zπ(s, a)를 나타내기 위해 신경망을 사용했었다. Dist-DQN은 대신 State-Action 쌍이 주어진 Q-value의 확률 변수를 나타내는 distribution Zπ(s, a) 을 사용한다.
먼저 Value Distribution를 표현하고 활용하는 방법부터 시작하겠다. 확률 이론 섹션에서 했던 것처럼, 우리는 두 개의 numpy 배열을 사용하여 Reward에 대한 이산 확률 분포를 나타낸다. 하나의 numpy 배열은 가능한 사건 (즉, 분포의 서포트, support of the distribution)이고 다른 하나는 각 관련 사건의 확률을 저장하는 동일한 크기의 배열이다. 서포트 배열과 확률 배열 사이의 내적을 취하면 분포의 기대값인 Reward를 얻는다.
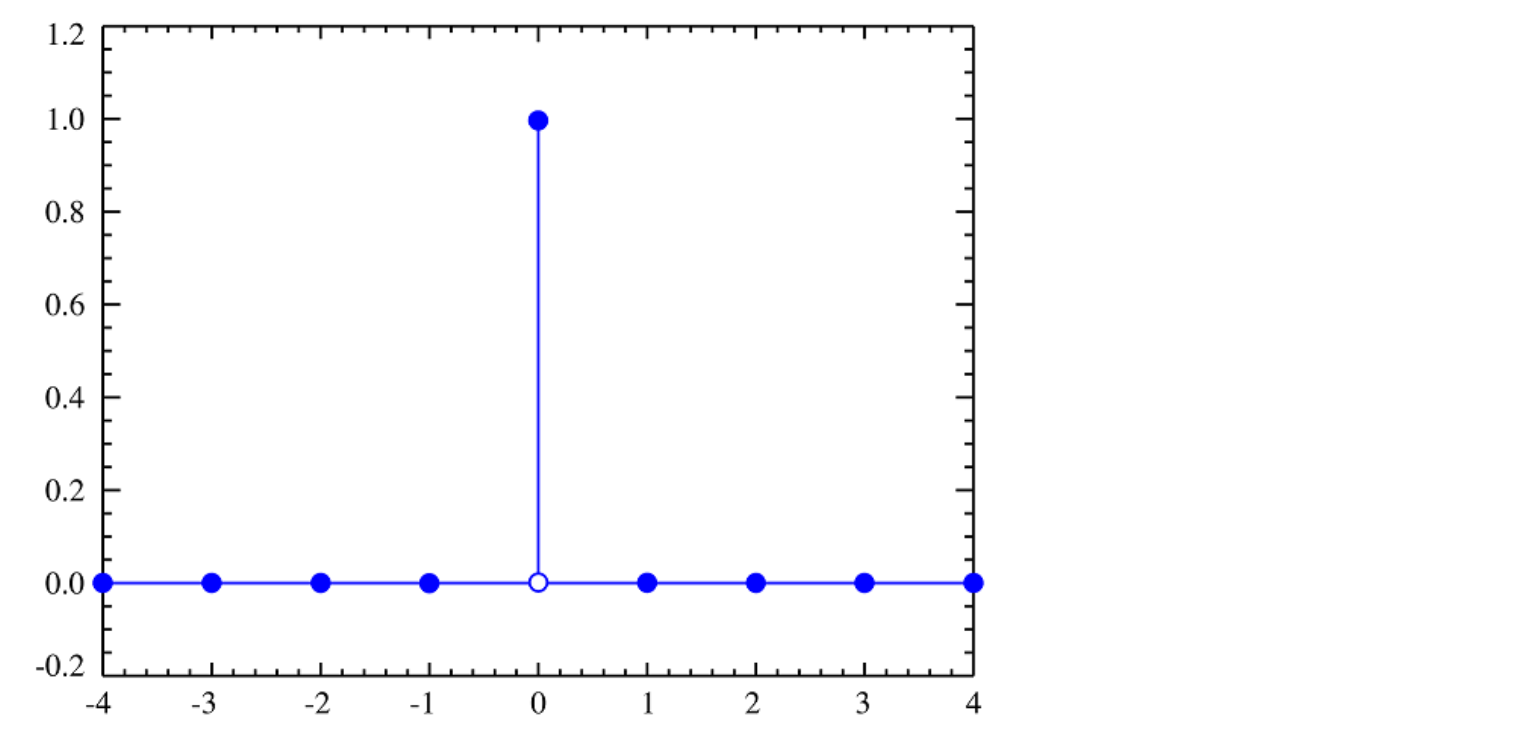
Figure7.9: 이것은 가능한 모든 값에 하나의 값(0)을 제외하고 0의 확률이 할당되기 때문에 퇴화 분포(Degenerate Distribution)입니다. 확률 0에 지정되지 않은 표본 값을 확률 분포의 서포트(Support)이라고합니다. 이 퇴화 분포는 1요소(값 0)를 서포트를 가진다.
Value Distribution Zπ(s, a)를 나타내는 방식의 한 가지 문제는 배열이 유한 크기이므로 유한한 수의 결과만 나타낼 수 있다는 것이다. 경우에 따라 보상은 일반적으로 고정된 유한 범위 내에서 제한되지만 주식 시장에서 얻거나 잃는 금액은 이론적으로 범위의 제한이 없다. 그러나 우리의 방법으로 표현할 수 있는 최소값과 최대값을 선택해야 한다. 이 제한은 Dabney et al 2017의 후속 논문 “Distributional Reinforcement Learning with Quantile Regression” 에서 해결되었다.이 장의 마지막 부분에서 이들의 접근 방식에 대해 간략히 설명하겠다.
Freeway의 경우 서포트가 -10과 +10 사이로 제한됩니다. 우리는 Terminal State가 아닌 (즉, 게임에서 이긴 경우 또는 진 경우의 State) 모든 time steps에서 도로을 건너는 데 너무 많은 시간을 허비하지 못하게 하기 위해 -1의 Reward을 받는다. 닭이 도로를 성공적으로 통과하면 +10, 게임이 중단되면 -10을 보상한다 (제한된 시간안에 닭이 도로를 건너지 못한 경우).
우리의 Dist-DQN은 128 요소 벡터인 State를 취하게 되며 3가지 가능한 Action(UP, DOWN, NO-OP) 각각에 대한 서포트와 확률 분포를 나타내는 3개의 분리된 동일한 크기의 텐서를 반환한다. 우리는 51 요소 서포트를 사용할 것이므로, 서포트 및 확률 텐서는 51 요소가 될 것이다. 에이전트가 임의로 초기화된 Dist-DQN으로 게임을 시작하고 “UP” Action을 취하고 -1의 Reward를 받는 경우 Dist-DQN을 어떻게 업데이트할까? 목표 분포(Target Distribution)는 무엇이며 두 분포 사이의 손실 함수는 어떻게 계산할까? 후속 상태 st + 1에 대해 Dist-DQN이 반환하는 모든 분포를 사전 분포로 사용하고 관찰된 rt 주위에 분포가 약간 재분포되도록 사전 분포를 업데이트합니다.
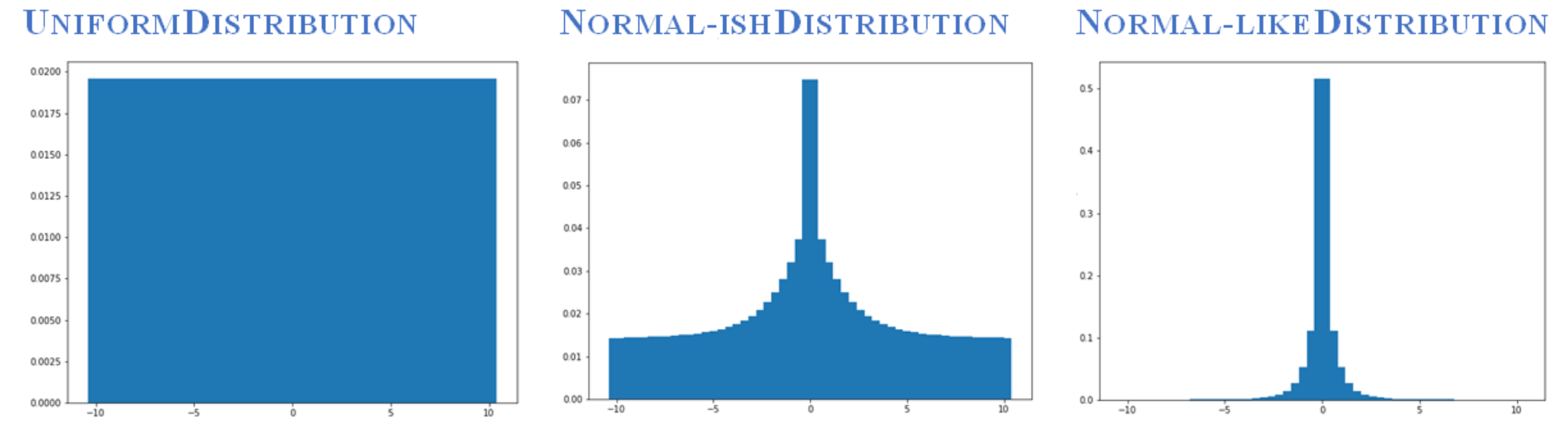
Figure 7.10 : 이산 분포를 입력받고 관찰된 보상에 따라 업데이트하는 함수를 만들었다. 이 함수는 사전 분포를 사후 분포로 업데이트하여 일종의 대략적인 베이지안 추론을 수행한다. 왼쪽의 Uniform Distribution에서 시작하여 일부 보상을 관찰하고 중간에 0 지점이 최정점인 distribution를 얻은 다음 더 많은 보상을 관찰한 후(모두 0) 분포는 오른쪽 그림과 같이 좁고 정상적인 분포가 된다.
Uniform Distribution로 시작하여 rt = −1을 관찰했을 때 사후 분포는 더 이상 균일(Uniform)하지 않아야하지만 여전히 균일(Uniform)에 가까워야 한다. 동일한 State에서 rt = -1을 반복해서 관찰하는 경우에만 분포가 -1 부근에서 강하게 피크를 치기 시작해야 한다. 일반적인 Q-learning 에 있어서 할인율 γ (감마)는 미래의 Reward가 현재 State의 가치에 얼마나 기여 하는지를 제어한다. Distributional Q-learning 에서 γ 매개 변수는 관측된 Reward에 대해 사전 분포를 얼마나 업데이트 할 것인지를 제어하여 유사한 기능을 수행한다.
우리가 미래를 많이 할인한다면, 최근에 관측된 Reward을 중심으로 할 것이다. 우리가 미래를 약하게 할인한다면, 관측된 Reward은 사전 분포 Z(St + 1, A t + 1)를 약간만 업데이트 할 것입니다. Freeway는 처음에 희박한(Sparse) Positive Reward을 가지고 있기 때문에 (예 : 게임에서 첫번째로 이긴 경우를 보기 전까지 많은 Action을 취해야 함) 감마 분포를 설정하여 사전 분포에 대해 약간만 업데이트한다.
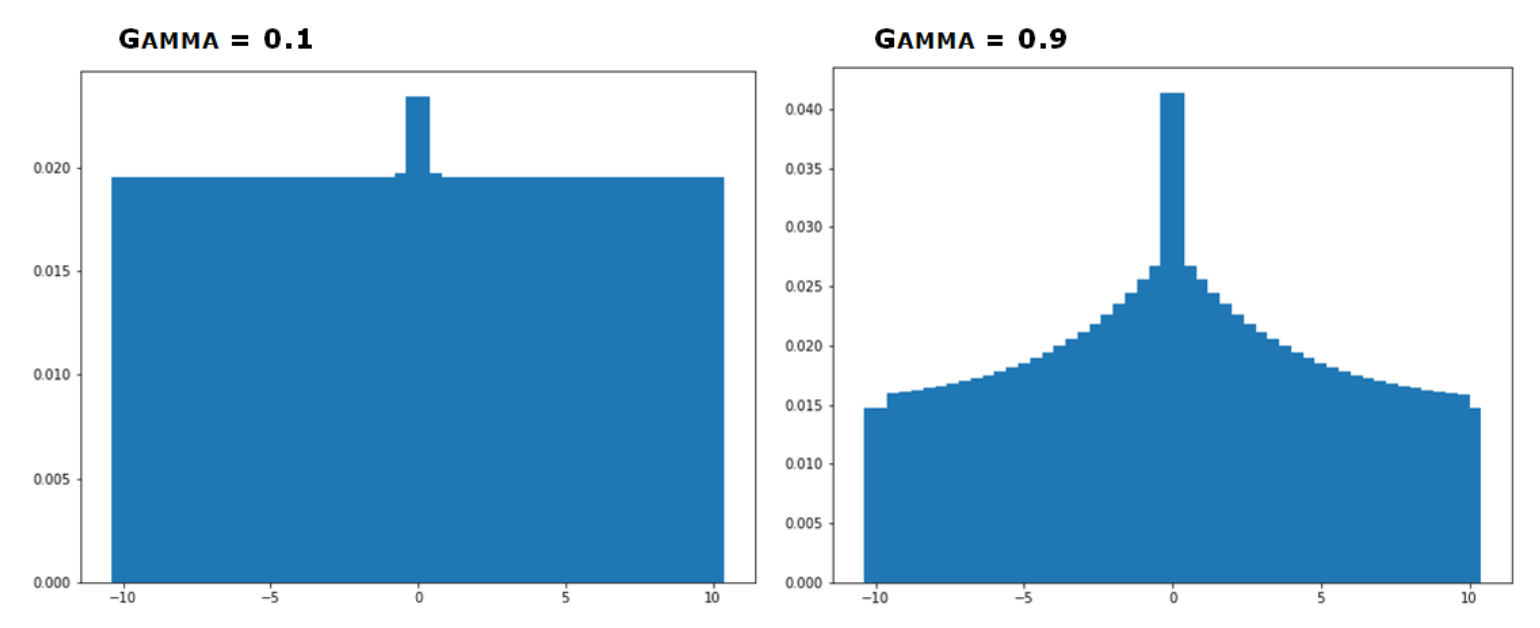
Figure 7.11 :이 그림은 감마(할인 계수, Discount Factor) 의 값에 따라 Uniform Distribution이 어떻게 변하는 지 보여준다.
Listing 7.1 Numpy에서 이산 확률 분포 설정
import torch
import numpy as np
from matplotlib import pyplot as plt
vmin,vmax = -10.,10. #A
nsup=51 #B
support = np.linspace(vmin,vmax,nsup) #C
probs = np.ones(nsup)
probs /= probs.sum()
z3 = torch.from numpy(probs).float()
plt.bar(support,probs) #D
#A 분포 서포트의 최소값과 최대값을 설정한다.
#B 서포트의 요소 수를 설정한다.
#C -10에서 +10 사이의 균등 간격 값의 Tensor인 서포트 Tensor를 만든다.
#D 분포를 Bar 플롯으로 시각화한다.
이제 분포를 어떻게 업데이트하는 지 보자. 사전 분포와 관측된 Reward을 받고 사후 분포를 리턴하는 update_dist(z, reward) 함수를 구해야 한다. 서포트는 -10에서 10 사이의 벡터이기 때문에 아래와 같다. :
array([-10. , -6.4, -2.8, 0.8, 4.4, -9.6, -6. , -2.4, 1.2, 4.8,
-9.2, -5.6, -2. , 1.6, 5.2, -8.8, -5.2, -1.6, 2. , 5.6,
-8.4, -4.8, -1.2, 2.4, 6. , -8. , -4.4, -0.8, 2.8, 6.4,
-7.6, -4. , -0.4, 3.2, 6.8, -7.2, -3.6, 0. , 3.6, 7.2,
-6.8, -3.2, 0.4, 4. , 7.6, 8. , 8.4, 8.8, 9.2, 9.6, 10. ])
서포트 벡터에서 관찰된 Reward에 가장 가까운 서포트 요소를 찾을 수 있어야 한다. 예를 들어, rt = −1을 관찰하면 가장 가까운 (동일한) 서포트 요소이므로 이를 -1.2 또는 -0.8에 매핑하려고 한다. 더 중요한 것은 확률 벡터에서 해당 확률을 얻을 수 있도록 이러한 서포트 요소의 인덱스를 원한다는 것이다. 서포트 벡터는 정적이므로 업데이트하지 않는다. 해당 확률만 업데이트한다.
각 서포트 요소가 가장 가까운 이웃에서 0.4 떨어져 있음을 알 수 있다. numpy linspace 함수는 균등한 간격의 요소 시퀀스를 생성하며 간격은 vmax-vmin / N-1에 의해 지정된다. 여기서 N은 서포트 요소의 수이다. 10, −10 및 N = 51을 해당 공식에 꽂으면 간격이 0.4가 된다. 이 값을 dz (delta Z)라고 하며 방정식 bj = (r-vmin) / dz 로 가장 가까운 서포트 요소 인덱스 값을 찾는 데 사용한다. 여기서 bj는 인덱스 값이다. bj는 소수 일 수 있고 인덱스는 음이 아닌 정수 이어야하므로 np.round (…)를 사용하여 가장 가까운 정수로 값을 반올림한다. 또한 최소 및 최대 지원 범위를 벗어나는 값을 클리핑해야 한다. 예를 들어 관찰 된 rt = -2이면 bj = −2− (−10) /0.4=−2+10 / 0.4 = 20입니다. 색인 20의 서포트 요소가 -2임을 알 수 있다. 이 경우는 관측된 Reward와 정확히 일치한다(반올림 필요 없음). 그런 다음 인덱스를 사용하여 -2 서포트 요소에 해당하는 확률을 찾을 수 있다.
관찰된 Reward에 해당하는 서포트 요소의 인덱스 값을 찾아 확률 질량(Probability Mass)의 일부를 해당 서포트와 주변 서포트 요소에 재분배하려고 한다. 우리는 최종 확률 분포가 실제 분포이고 1에 합산되도록 주의해야 한다. 우리가 할 일은 단순히 왼쪽과 오른쪽에 있는 이웃들로부터 확률 질량의 일부를 취하여 관측된 Reward의 해당하는 요소에 추가하는 것이다. 그런 다음 가장 가까운 이웃은 Figure 7.12에 표시된 것처럼 가장 가까운 이웃 등에서 확률 질량을 훔친다. 그러나 훔친 확률이 많아 질수록 관측된 Reward 주변의 확률은 지수적으로 작게 될 것이다.
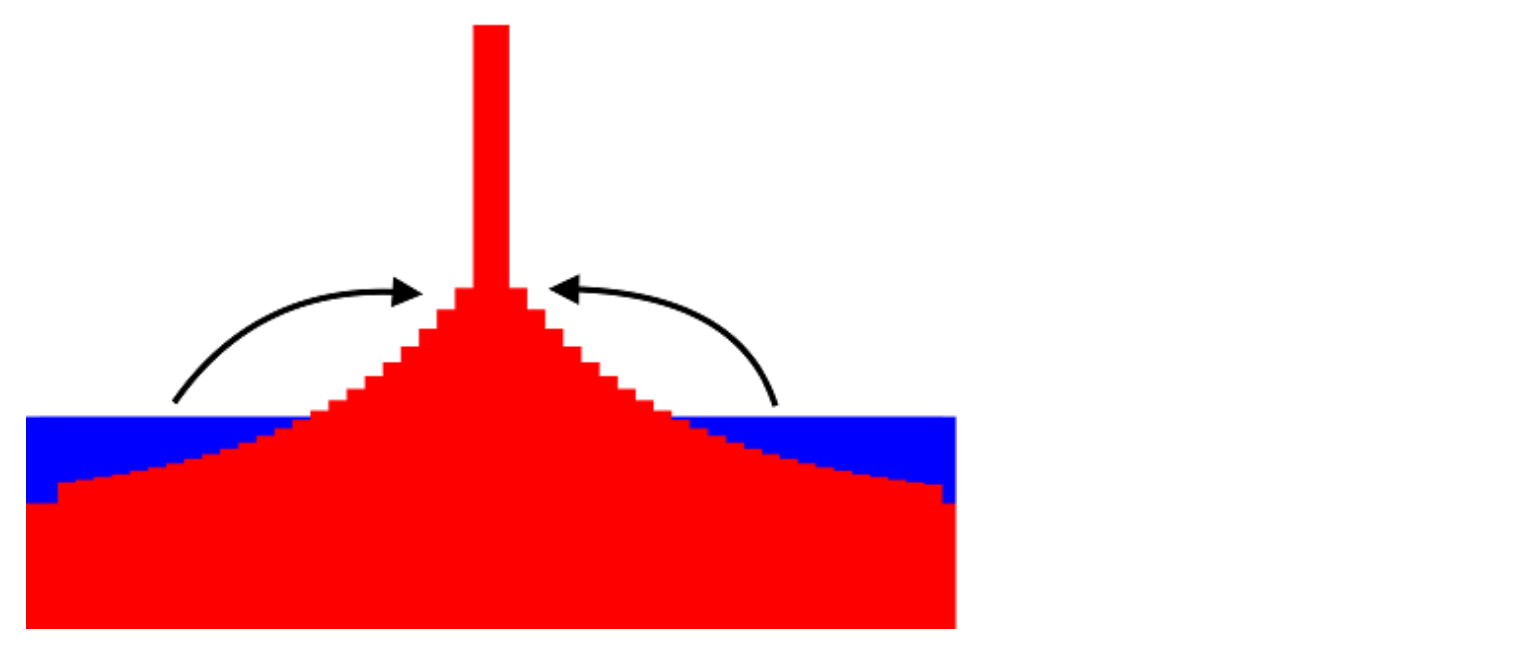
Figure7.12 : update_dist 함수는 이웃으로부터 관측된 Reward 값으로 확률을 재분배한다.
아래에서는 일련의 서포트, 관련 확률 및 관측치를 취하고 확률 질량을 관측 값으로 재분배하여 업데이트된 확률 분포를 반환하는 함수를 구현한다.
Listing 7.2 확률 분포 업데이트
def update dist(r,support,probs,lim=(-10.,10.),gamma=0.8):
nsup = probs.shape[0]
vmin,vmax = lim[0],lim[1]
dz = (vmax-vmin)/(nsup-1.) #E
bj = np.round((r-vmin)/dz) #F
bj = int(np.clip(bj,0,nsup-1)) #G
m = probs.clone()
j=1
for i in range(bj,1,-1): #H
m[i] += np.power(gamma,j) * m[i-1]
j += 1
j=1
for i in range(bj,nsup-1,1): #I
m[i] += np.power(gamma,j) * m[i+1]
j += 1
m /= m.sum() #J
return m
#E 서포트 간격을 계산한다.
#F 서포트에서 관찰된 Reward의 인덱스 값을 계산한다.
#G 서포트에 유효한 인덱스 값인지 확인하기 위해 값을 반올림하고 클리핑한다.
#H 바로 왼쪽 이웃에서 시작하여 확률의 일부를 훔칩니다.
#I 바로 오른쪽 이웃에서 시작하여 확률의 일부를 훔칩니다.
#J 전체 합계로 나누어 확률의 합이 1이 되도록 한다.
작동 원리를 알아보기 위해 이 메커니즘을 살펴 보겠다. Uniform 사전 분포로 시작한다.
>>> probs
array([0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.01960784, 0.01960784, 0.01960784, 0.01960784, 0.01960784,
0.0196078])
각 서포트의 확률은 약 0.02이다. rt = −1을 관찰하고 bj ≈ 22를 계산한다. 그런 다음 ml와 mr로 표시된 가장 가까운 왼쪽 및 오른쪽 이웃을 각각 21과 23의 인덱스로 찾는다. 그런 다음 ml에 γj를 곱한다. 여기서 j는 1부터 시작하여 1 씩 증가하는 값이다. 그러면 지수적으로 감소되는 감마 시퀀스가 나타난다. 예를 들어 γ1, γ2, … γj.
감마는 0과 1 사이의 값이어야 하므로 감마의 시퀀스는 γ = 0.5 인 경우 0.5, 0.25, 0.125, 0.0625 이다. 먼저 왼쪽과 오른쪽 이웃에서 0.5 * 0.02 = 0.01을 취하여 bj = 22의 기존 확률인 0.02도 추가합니다. 따라서 bj = 22에서의 확률은 0.01 + 0.01 + 0.02 = 0.04가 된다.
이제 왼쪽 이웃 ml는 인덱스 20에서 자신의 왼쪽 이웃에서 확률 질량을 훔치지만, 우리가 γ2를 곱하기 때문에 덜 훔친다. 오른쪽 이웃 mr은 오른쪽 이웃을 훔쳐서 같은 일을 한다. 각 요소는 배열의 끝에 도달 할 때까지 왼쪽 또는 오른쪽 이웃에서 훔친다. 감마가 0.99와 같이 1에 가까우면 많은 확률 질량이 rt에 가까운 서포트에 재분배된다. 그러면 분포 업데이트 기능을 테스트 해 보겠다. Uniform 분포에서 시작하고 -1의 Reward를 제공한다.
Listing 7.3 단일 관측 후 확률 질량(Probability Mass) 재분배
ob_reward = -1
Z = torch.from_numpy(probs).float()
Z = update_dist(ob_reward,torch.from_numpy(support).float(),
Z,lim=(vmin,vmax),gamma=0.1)
plt.bar(support, Z)
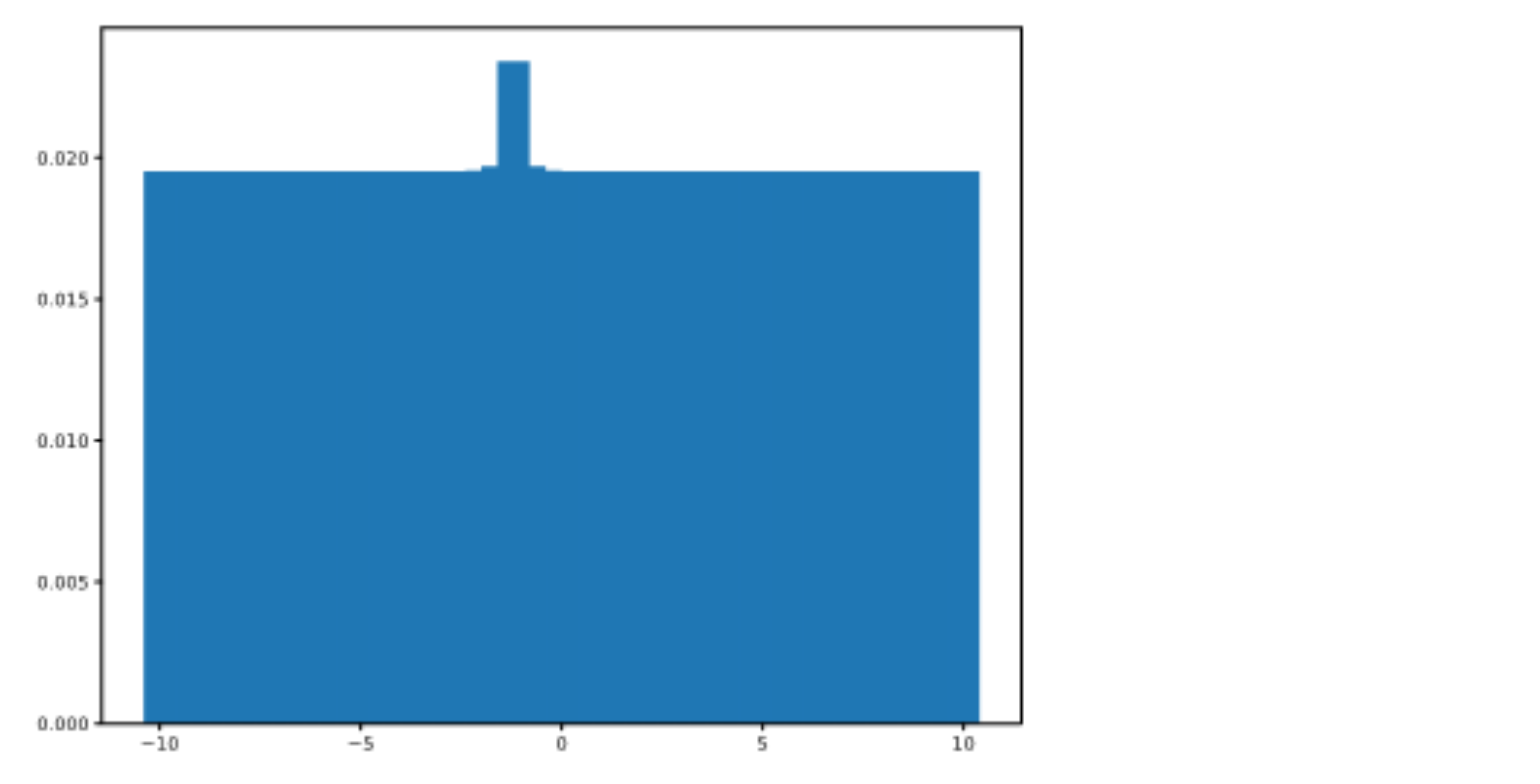
분포가 여전히 균등하지만 -1을 중심으로 뚜렷한“범프(돌출부)”가 있음을 알 수 있다. 할인율이 γ 인 경우 이 범프의 크기를 제어 할 수 있다. 직접 업데이트를 변경하는 해 보려면 감마 변경을 시도한다. 이제 다양한 연속된 Reward를 에 대해서는 분포가 어떻게 변하는 지 보자. Multi-modality를 관찰 할 수 있어야 한다.
Listing 7.4 연속된 Reward 관측 후 확률 질량(Probability Mass) 재분배
ob_reward = [10,10,10,0,1,0,-10,-10,10,10]
for i in range(len(ob_rewards)):
Z = update_dist(ob_reward[i],torch.from_numpy(support).float(),
Z,lim=(vmin,vmax),gamma=0.5)
plt.bar(support, Z)
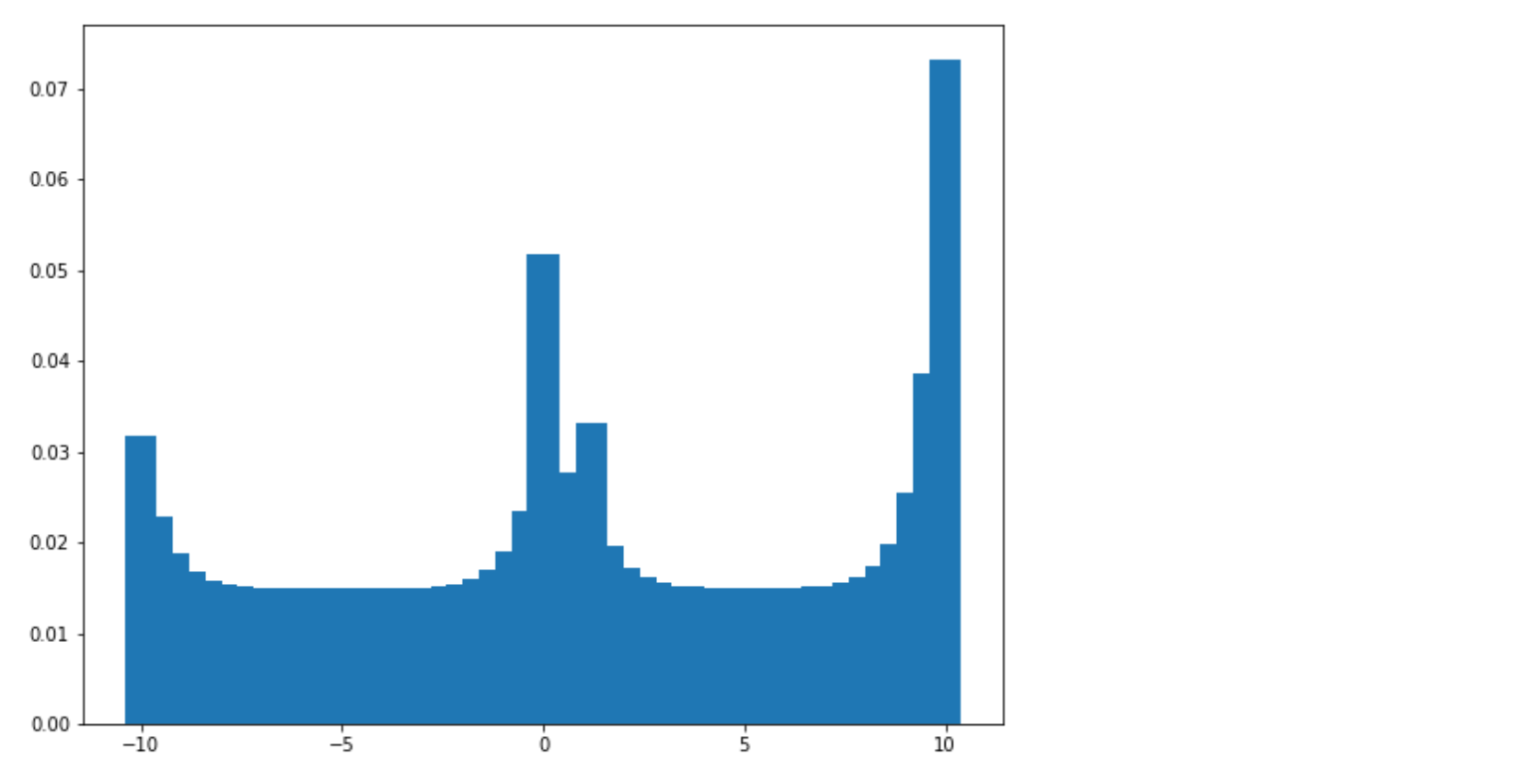
이제 4 개의 서로 다른 종류의 Reward, 즉 10, 0, 1 및 -10에 해당하는 다양한 높이의 피크가 4 개 있음을 알 수 있다. 가장 높은 피크 (분포의 최빈값)는 가장 자주 관찰되는 Reward이므로 10에 해당한다. 이제 Uniform 사전 분포에서 동일한 Reward를 여러 번 관찰하면 분산이 어떻게 감소하는지 보자.
Listing 7.5 연속된 동일한 Reward 관측 후 감소된 분산
ob_reward = [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]
for i in range(len(ob_rewards)):
Z = update_dist(ob_reward[i],torch.from_numpy(support).float(),
Z,lim=(vmin,vmax),gamma=0.5)
plt.bar(support, Z)
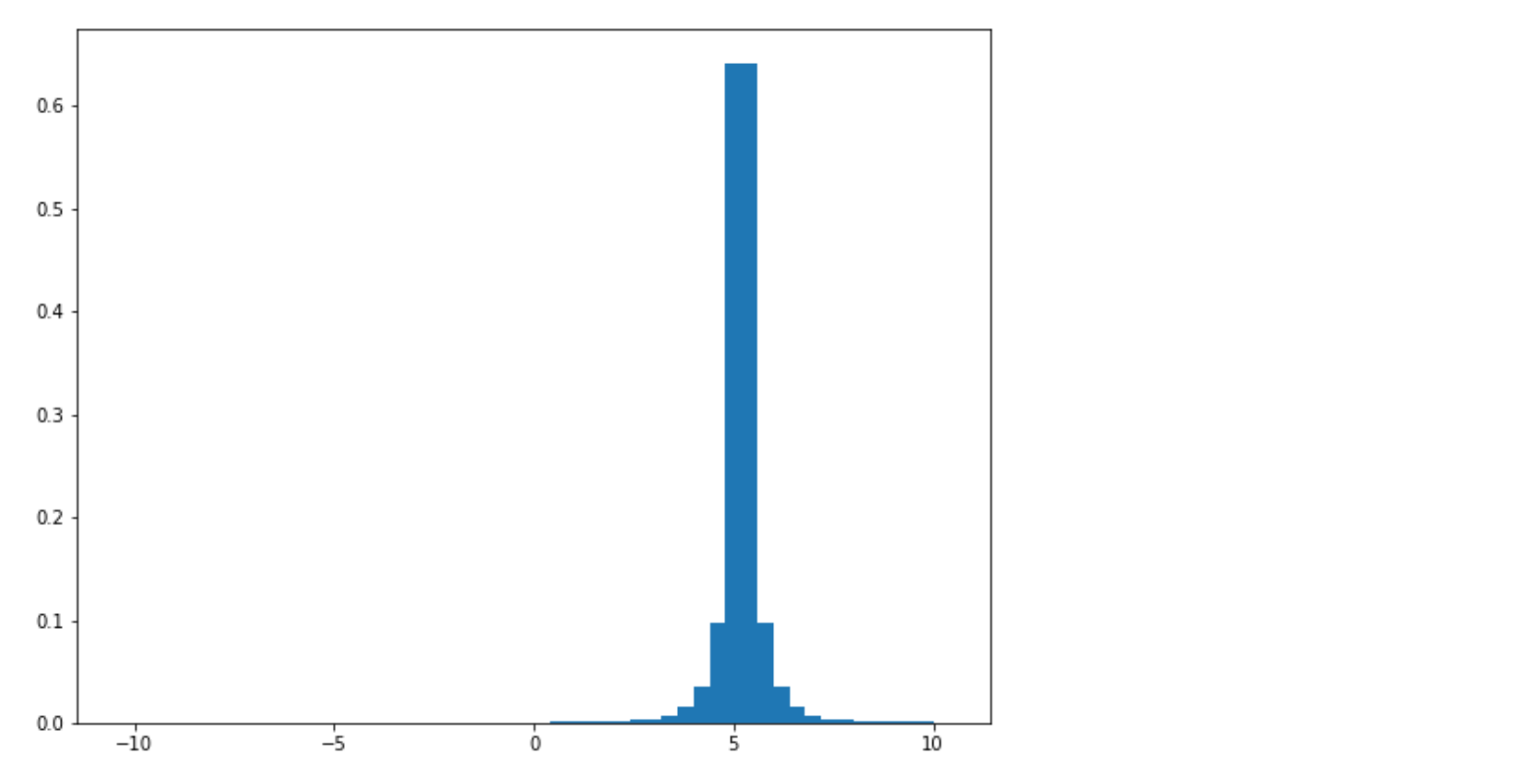
Uniform 분포가 5를 중심으로 하는 정규 분포로 분산이 훨씬 적은 것을 볼 수 있다. 이 함수를 사용하여 Dist-DQN이 근사하는 법을 학습한 목표 분포(Target Distribution)를 만들어 낸다. 지금 Dist-DQN을 만들어 보자.
7.4.2 Dist-DQN 구현하기
앞에서 간략히 이야기했듯이 Dist-DQN은 128 요소 State 벡터를 가져 와서 Dense Feedfoward 레이어 몇 개를 통과한 다음 for-loop를 사용하여 마지막 레이어에 3개의 개별 행렬을 곱하여 3개의 벡터를 구한다.마지막으로 softmax 함수를 적용하여 유효한 확률 분포인지 확인한다. 3개의 다른 출력 Head를 가진 신경망이다. 이 3개의 출력 분포를 단일 3 × 51 행렬로 수집하여 Dist-DQN의 최종 출력으로 반환한다. 따라서 출력 행렬의 특정 행을 인덱싱하여 특정 동작에 대한 개별 Action-value 분포를 얻을 수 있다. Figure 7.13은 전체 아키텍처 및 텐서 변환을 보여준다.
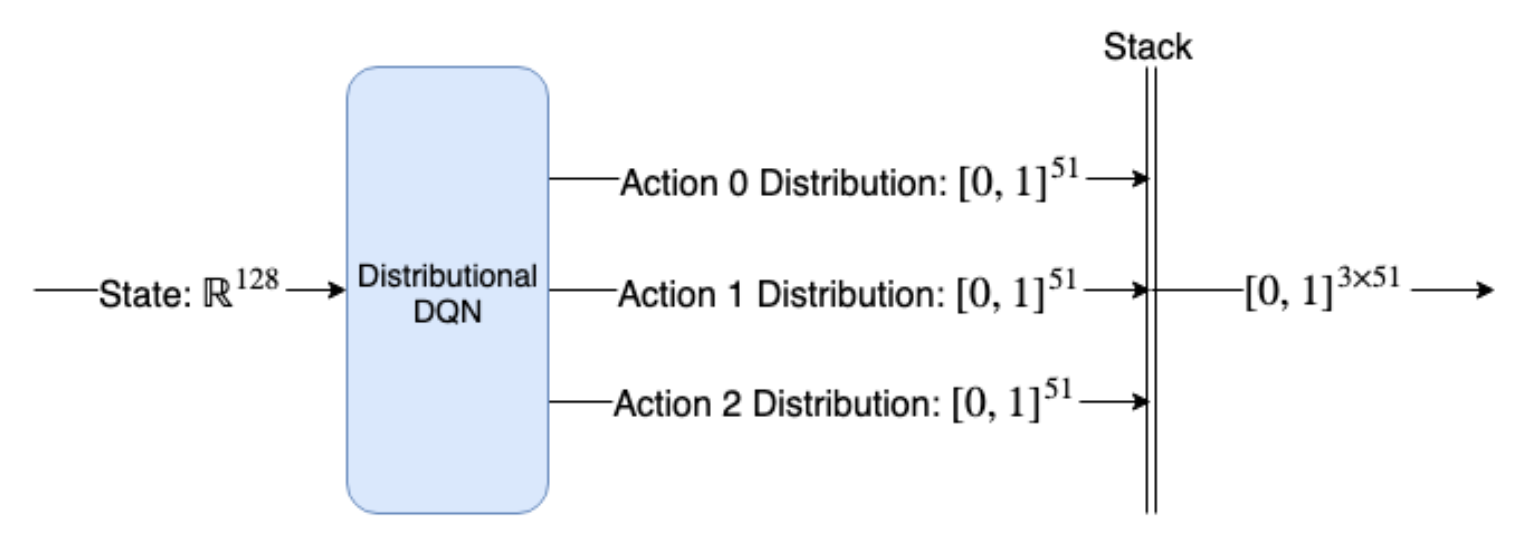
Figure 7.13 : Distributional DQN (Dist-DQN) 은 128 요소 State 벡터를 입력으로 받고 3개의 개별 51 요소 확률 분포 벡터를 생성한 후 단일 3 x 51 행렬로 반환한다.
Listing 7.6 Distributional DQN
def dist_dqn(x,theta,aspace=3): #A
dim0,dim1,dim2,dim3 = 128,100,25,51 #B
t1 = dim0*dim1
t2 = dim2*dim1
theta1 = theta[0:t1].reshape(dim0,dim1) #C
theta2 = theta[t1:t1 + t2].reshape(dim1,dim2)
l1 = x @ theta1 #D
l2 = l1 @ theta2 #E
l2 = torch.selu(l2)
l3 = []
for i in range(aspace): #F
step = dim2*dim3 _
theta5 = theta[theta5_dim:theta5_dim+step].reshape(dim2,dim3)
l3_ = l2 @ theta5 #G
l3.append(l3_)
l3 = torch.stack(l3,dim=1) #H
l3 = torch.nn.functional.softmax(l3,dim=2)
return l3.squeeze()
#A`x`는 128 요소 벡터 State 이고,`theta`는 매개 변수 벡터이며, 'aspace' 는 Action 공간의 크기이다.
#B 레이어 크기를 정의하여 적절한 크기의 행렬을 정의한다.
#C `theta`의 첫 부분을 첫 번째 레이어 행렬에 unpack한다.
#D 이 계산의 차원은 B × 128 × 128 × 100 = B × 100 이다. 여기서`B`는 배치 크기이다.
#E 이 계산의 차원은 B × 100 × 100 × 25 = B × 25 이다.
#F 각 Action-value 분포를 생성하기 위해 각 Action을 반복한다.
#G 이 계산의 차원은 B × 25 × 25 × 51 = B × 51 이다.
#H 마지막 레이어의 차원은 B × 3 × 51 이다.
이 장에서는 그라디언트 디센트 (gradient descent)를 수동으로 수행하고,이를 쉽게하기 위해 Dist-DQN은 ‘세타 (theta)’라는 단일 매개 변수 벡터를 받아 들여 적절한 크기의 여러 개별 레이어 행렬로 압축을 풀고 형태를 변경한다. 이는 여러 개별 엔터티가 아닌 단일 벡터에서 그래디언트 디센트를 수행 할 수 있기 때문에 더 쉽다. 또한 DQN 에서 했던 것처럼 Fixed-Q Target Network를 사용할 것이므로theta의 사본을 보관하고 동일한 dist_dqn 함수에 전달하기만 하면 된다.
다른 새로운 시도는 다중 출력 Head 입이다. 우리는 단일 출력 벡터를 반환하는 신경망에 익숙하지만 이 경우는 행렬을 반환하기를 원한다. 이를 위해 우리는 ‘l2’에 3개의 개별 레이어 행렬를 곱하여 3개의 서로 다른 출력 벡터를 생성하는 루프를 설정한다. 그 외에 총 5개의 Dense Layer가 있는 매우 간단한 신경망이다.
이제 Dist-DQN의 출력, Reward 및 Action을 취한 다음 신경망에 더 가까워 지도록 목표 분포(Target Distribution)를 생성하는 function 이 필요하다. 이 함수는 앞에서 사용한 update_dist 함수를 사용하지만 실제로 수행된 작업과 관련된 분포만 업데이트하려고 한다. 또한 DQN 에서 배운대로 Terminal State에 도달하면 다른 Target이 필요하다. Terminal State에서 정의된 미래의 Reward가 없기 때문에 Expected Reward는 관찰된 Reward이다. 이는 Bellman 업데이트가 Z(st, at) ← R(St, At)로 감소함을 의미한다. 우리는 관찰한 단일 Reward만 있고 업데이트할 사전 분포가 없으므로 Target은 퇴화 분포(Degenerate Distribution)가 된다. 그것은 모든 확률 질량이 단일 값에 집중되어 있는 분포에 대한 용어이다.
Listing 7.7 Target Distribution 계산
def get_target_dist(dist_batch,action_batch,reward_batch,support,
lim=(-10,10),gamma=0.8):
nsup = support.shape[0]
vmin,vmax = lim[0],lim[1]
dz = (vmax-vmin)/(nsup-1.)
target_dist_batch = dist_batch.clone()
for i in range(dist batch.shape[0]): #A
dist_full = dist_batch[i]
action = int(action batch[i].item())
dist = dist_full[action] r = reward_batch[i]
if r != -1: #B
target_dist = torch.zeros(nsup)
bj = np.round((r-vmin)/dz)
bj = int(np.clip(bj,0,nsup-1))
target_dist[bj] = 1.
else: #C
target_dist = update_dist(r,support,dist,lim=lim,gamma=gamma)
target_dist_batch[i,action,:] = target_dist #D
return target_dist_batch
#A 배치 차원을 통한 루프
#B Reward가 -1이 아닌 경우 Terminal State이며 Target은 Reward 값의 퇴화 분포(Degenerate Distribution)이다.
#C State가 Terminal State가 아닌 경우 Target 분포는 이전에 제공된 Reward에 대한 베이지안 업데이트이다.
#D 수행된 Action의 분포만 변경한다.
get_target_dist 함수는 Shape가 B × 3 × 51의 Batch를 취한다. 여기서 ‘B’는 Batch 차원이며 동일한 크기의 텐서를 반환한다. 예를 들어 Batch가 1일때의 예 (예 : 1 × 3 × 51)가 있고 에이전트가 Action 1을 수행하고 -1의 Reward를 얻었을 경우 이 함수는 1 × 3 × 51 텐서를 반환합니다. (차원 1의) 인덱스 1과 연관된 1 x 51 분포는 -1의 관측된 Reward을 사용하여 update_dist 함수에 따라 변경된다. 관측된 Reward가 10 인 경우, Action 1과 연관된 1 x 51 분포는 10의 Reward와 관련된 것(인덱스 50)을 제외한 모든 요소의 확률이 0 인 퇴화 분포(Degenerate Distribution)로 업데이트된다.
7.5 확률 분포 비교하기
이제 Dist-DQN과 목표 분포를 생성 할 수 있는 방법이 있으므로, 예측된 Action-value 분포가 목표 분포와 어떻게 다른지 계산하는 손실 함수가 필요하다. 그런 다음 평소와 같이 역전파 및 경사 하강을 수행 할 수 있고 Dist-DQN 파라미터를 보다 정확하게 업데이트한다. 우리는 종종 스칼라 또는 벡터로 이루어진 두 배치의 사이의 거리를 최소화하려고 할 때 평균 제곱 오차(MSE) 손실 함수를 사용하지만 이것은 두 확률 분포 사이의 적절한 손실 함수가 아니다. 실제로 확률 분포 사이의 손실 함수에 대한 많은 선택이 있다. 우리는 두 확률 분포의 차이를 측정하고 그 거리를 최소화하는 함수가 필요하다.
기계 학습에서 일반적으로 일부 데이터 세트의 경험적 데이터와 밀접하게 일치하는 데이터를 예측하거나 생성하기 위해 파라메트릭 모델(Parametric Model) (예 : 신경망)을 훈련하려고 한다. 확률적으로 생각할 때 우리는 합성 데이터를 생성하고 점점 더 현실적인 데이터, 즉 일부 경험적 데이터 세트와 매우 유사한 데이터를 생성하도록 신경 네트워크를 훈련시키는 것으로 신경 네트워크를 생각할 수 있다. 이것이 우리가 생성 모델(Generative Model), 즉 데이터를 생성하는 모델을 훈련시키는 방법이다. 생성된 데이터가 일부 학습(경험, Empirical) 데이터셋과 매우 유사하게 보이도록 매개 변수를 업데이트하여 학습한다.
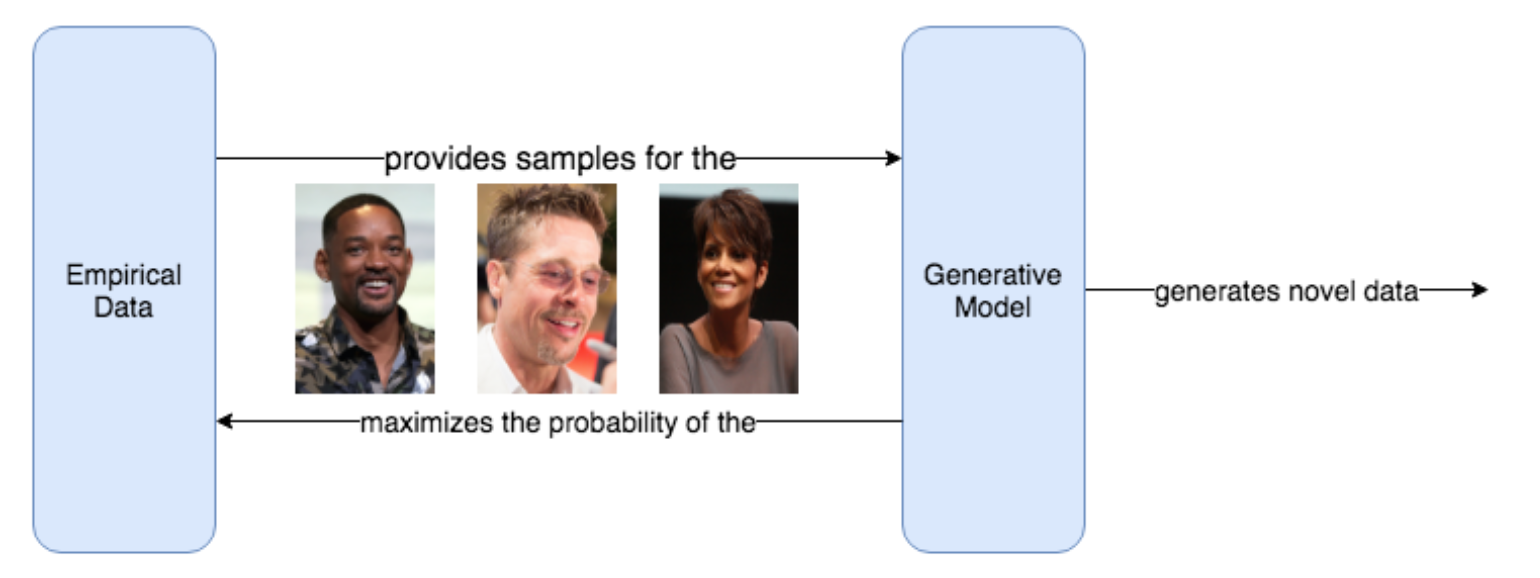
Figure 7.14: 생성 모델은 경험적 데이터셋 과 유사한 샘플을 생성할 확률을 최대화하여 학습하는 확률 모델이 될 수 있다. 학습 전에는, 생성 모델이 학습 데이터셋으로 부터 취한 데이터 예들에 대해 낮은 확률을 할당할 것이다. 생성 모델의 학습 목적은 생성 모델이 데이터셋으로 부터 도출된 데이터 예들에 높은 확률을 할당하여 새로운 샘플을 생성하는 것이다. 학습은 경험적 데이터가 생성 모델에 제공되는 반복 루프에서 이루어 지며, 이는 경험적 데이터의 확률을 최대화하려고 시도한다. 충분히 반복 후에 생성 모델은 경험적 데이터에 높은 확률을 할당 할 것이므로 이 분포에서 데이터를 샘플링한다면 새로운 합성 데이터를 생성 할 수 있다.
예를 들어 유명인의 얼굴 이미지를 생성하는 생성 모델을 만들고 싶다고 가정해 보겠다. 이를 위해서는 학습 데이터가 필요하므로 Will Smith, Britney Spears와 같은 다양한 유명인의 수십만 개의 고품질 사진이 포함된 무료 CelebA 데이터셋을 사용한다. 생성 모델 P와 이 경험적 데이터셋 Q를 설명에 사용해 보겠다.
이제 데이터셋 Q의 이미지는 실세계에서 샘플링되었지만 실세계에는 데이터 세트에 포함되지 않은 무한한 사진들이 있으며 그 중에 일부인 작은 샘플일 뿐이다. 예를 들어 데이터 집합에 Will Smith의 헤드 샷 사진이 하나만 있을 수도 있고 다른 각도에서 촬영한 Will Smith의 다른 사진들이 데이터셋에 포함되었을 수도 있다. 그러나 아기 코끼리가 머리 위에 있는 Will Smith의 사진은 불가능하지는 않지만 존재하지 않을 가능성이 높기 때문에 데이터 세트에 포함될 가능성이 적다(누가 사람 머리에 아기 코끼리를 놓겠는가?).
유명인 사진은 그렇게 많지 않으므로 실세계는 유명인 이미지에 대한 확률 분포를 갖는다. 유명인 사진의 실제 확률 분포를 Q(x)로 표시 할 수 있다. 여기서 x는 임의의 이미지이며 Q(x)는 해당 이미지가 실세계에 존재할 가능성을 알려준다. x가 데이터셋 Q에서 특정 이미지인 경우 해당 이미지가 실제 세계에 존재하기 때문에 Q(x) = 1.0 이다. 그러나 데이터셋에는 없지만 작은 샘플 외부의 실세계에 있는 이미지에 대해서 Q(x)는 0.9가 될 수 있다.
생성 모델 P를 무작위로 초기화하면 흰색 노이즈처럼 보이는 임의의 모양을 가진 이미지가 출력된다. 우리는 우리의 생성 모델을 확률 변수로 생각할 수 있고, 모든 확률 변수는 P(x)를 나타내는 확률 분포가 연관되어 있기 때문에 특정 이미지가 유명인 이미지일 확률이 현재의 Parameter의 집합에 얼마만큼 주어졌는지 생성 모델에 물어 볼 수 있다. 처음 초기화 할 때, 모든 이미지가 어느 정도 똑같을 가능성이 있으며 모든 것이 상당히 낮은 확률로 할당 될 것이라고 생각할 수 있다. P(“Will Smith photo”)를 물어 보면 아주 작은 확률을 반환하지만 Q( “Will Smith Photo”)를 요청하면 1.0이 된다.
데이터셋 Q를 사용하여 사실적인 유명인 사진을 생성하도록 생성 모델 P를 학습시키기 위해, 우리는 생성 모델이 Q의 데이터 및 Q에는 없지만 타당한 데이터에 높은 확률을 할당하기를 바란다. 수학적으로 다음에 표시한 비율을 최대화하려고 한다.

이를 P(x)와 Q(x) 사이의 우도비(LR, Likelihood Ratio)라고 한다. 이 맥락에서 우도(Likelihood)는 확률(Probability)를 표현하는 또 다른 단어일 뿐이다. 학습되지 않은 P를 사용하여 Q에 존재하는 Will Smith의 이미지에 대한 비율을 취하면 다음과 같은 결과를 얻을 수 있다.
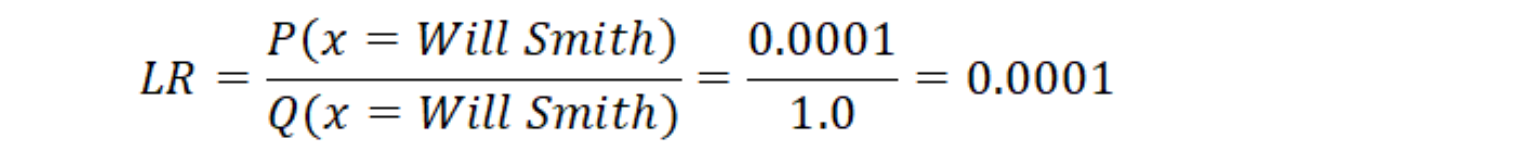
이경우 우도비가 매우 작다. 우리의 생성 모델로 역전파되어 이 비율이 최대화되도록 매개 변수를 업데이트하기 위해 경사 하강(Gradient Descent)을 수행하려고 한다. 이 우도비는 최대(또는 음수를 최소화)하기 위한목적 함수(Objective function)가 된다. 그러나 단일 이미지에 대해서만 이 작업을 수행하지 않고 생성 모델은 데이터셋 Q의 모든 이미지의 총 확률을 최대화하기를 원한다. 모든 개별 예의 곱을 취하여 이 총 확률을 찾을 수 있다 (왜냐하면 ‘A and B’의 확률은 A와 B가 독립(independent)이고 동일한 분포에서 나왔다는 가정하에서 A의 확률에 B의 확률을 곱하면 되기 때문이다). 새로운 목표 함수는 데이터셋의 각 데이터에 대한 우도비의 곱이다. 몇 가지 수학 방정식이 나오지만 기본 확률 개념을 설명하기 위해 사용하고 있으니 이를 기억하기 위해 시간을 소비하지 않기를 바란다.
Table 1.3: 우도비(Likelihood Ratio) 수학 공식 과 파이썬 코드
Math
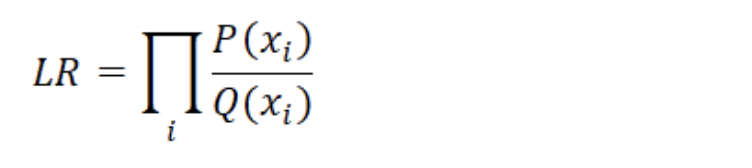
Python
p = np.array([0.1,0.1])
q = np.array([0.6,0.5])
def lr(p,q):
return np.prod(p/q)
이 목적 함수의 한 가지 문제점은 컴퓨터가 작은 부동 소수점 숫자를 완벽하게 처리하지 못하기 때문에 다수의 확률을 곱할 때 오류가 있다는 것이다. 컴퓨터는 표현할 수 있는 유한 한 수의 범위를 가지기 때문에 수치적으로 부정확하고 결과적으로 언더플로(Numerical Underflow)를 발생시킨다. 이 상황을 개선하기 위해 로그 확률(로그 우도, Log-Likelihood, Log-Probability)를 사용한다. 로그 함수는 매우 작은 값의 범위를 가지는 확률의 값을 음의 무한대 (확률에 있어서는 0)에서 최대값 0(확률에 있어서는 1)의 값의 범위로 바꾸어 준다.
로그는 또한 log(a⋅b) = log(a) + log(b) 라는 멋진 속성을 가지므로 곱셈을 덧셈으로 바꿀 수 있으며 컴퓨터는 수치적 불안정성 또는 오버플로 위험없이 훨씬 쉽게 계산 할 수 있다. 위의 공식을 로그 우도비(Log-Likelihood Ratio)로 변환 할 수 있다.
Table 1.4: 로그 우도비(Log-Likelihood Ratio) 수학 공식 과 파이썬 코드
Math
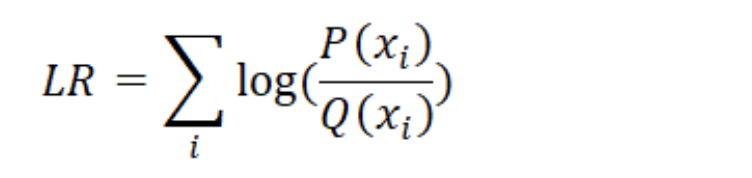
Python
p = np.array([0.1,0.1])
q = np.array([0.6,0.5])
def lr(p,q):
return np.sum(np.log(p/q))
로그 확률 버전은 계산이 더 간단하고 좋다. 그러나 또 다른 문제는 개별 샘플에 따라 다르게 가중치를 부여해야 한다는 것이다. 예를 들어, 데이터셋에서 Will Smith 이미지를 샘플링하면 유명인이 찍힌 사진은 유명인이 아닌 사진보다 확률이 높아야 한다. 우리는 모델이 실세계에서, 또는 경험적 분포 Q(x)와 관련하여 더 가능성이 높은 학습 이미지에 더 많은 비중을 두기를 원합니다. 따라서 각 로그 우도 비율에 Q(x) 확률을 가중치로 적용한다.
Table 1.5: 가중 로그 우도비(Weighted Log-Likelihood Ratio) 수학 공식 과 파이썬 코드
Math
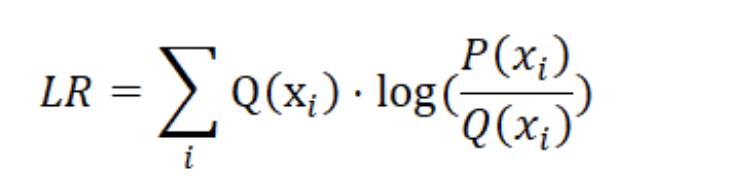
Python
p = np.array([0.1,0.1])
q = np.array([0.6,0.5])
def lr(p,q):
x = q * np.log(p/q)
x = np.sum(x)
return x
이제 생성 모델의 샘플이 실제 데이터 분포와 비교될 우도를 측정하는 객관적인 함수를 가지게 되었으며, 샘플이 실제 환경에 있을 가능성에 따라 가중된다. 마지막으로 작은 문제가 하나 있다. 로그 우도 비율을 높이기를 원하기 때문에 이 목적 함수를 최대화해야 하지만 편의성과 관례(convention)에 따라 오류 또는 손실 함수인 목적 함수를 최소화하는 것이 좋다. 음수 부호만 추가하면 이 문제를 해결할 수 있는데 이럴 경우 우도가 높을수록 오류나 손실은 작아지게 된다.
Table 1.6: 쿨백-라이블러 발산(Kullback-Leibler divergence)
Math
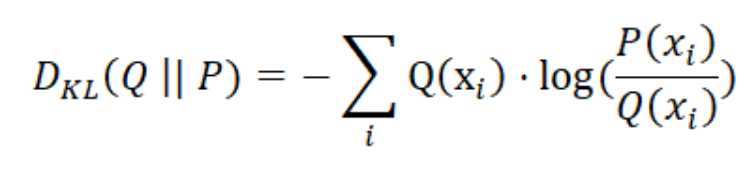
Python
p = np.array([0.1,0.1])
q = np.array([0.6,0.5])
def lr(p,q):
x = q * np.log(p/q)
x = -1 * np.sum(x)
return x
| LR이 이상한 기호 DKL (Q | P)로 바뀌었음 알아 챘을 것이다. 방금 만든 함수는 머신 러닝에서 매우 중요한 함수이며, 간단히 쿨백-라이블러 발산 또는 KL 발산이라고 한다. KL 발산은 확률 분포 사이의 일종의 오류 함수이다. 즉, 두 확률 분포가 어떻게 다른지 알려 준다. |
| 모델 생성 확률 분포(model generated probability distribution)와 실제 데이터의 경험적 분포(empirical distribution) 사이의 거리를 최소화하려고 하는 경우에 KL 발산을 최소화하면 된다. 방금 살펴본 바와 같이 KL 발산을 최소화하는 것은 경험적 데이터와 비교하여 생성된 데이터의 조인트 로그 우도 비율(Joint Log-Likelihood Ratio)을 최대화하는 것과 같습니다. KL 발산은 대칭(symmetric)이 아니므로 DKL (Q | P) ≠ DKL (P | Q)이라는 점이 중요하다. 이는 수학적 정의로 볼 때 명확하다. KL 발산은 비율을 포함하므로 비율이 둘 다 1이 아니면 (즉, a = b가 아닌 경우 a / b ≠ b / a) 역수와 같을 수 없다. |
KL 발산은 완벽한 목적 함수이지만 실제로는 목적에 따라 약간 단순화 할 수 있다. 일반적으로 log (a / b) = log (a) -log (b)를 상기해 보면 KL 발산을 다음과 같이 다시 작성할 수 있다.
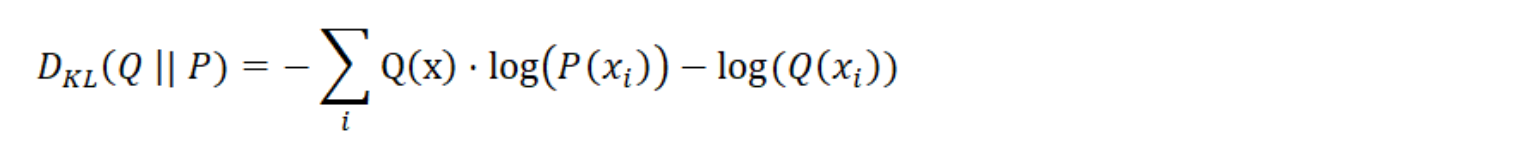
기계 학습에서는 모델을 최적화(오류를 줄이기 위해 모델의 매개 변수 업데이트) 만하고 경험적 분포 Q(x)는 변경할 수 없다. 따라서 왼쪽의 가중 로그 확률에만 관심이 있다.
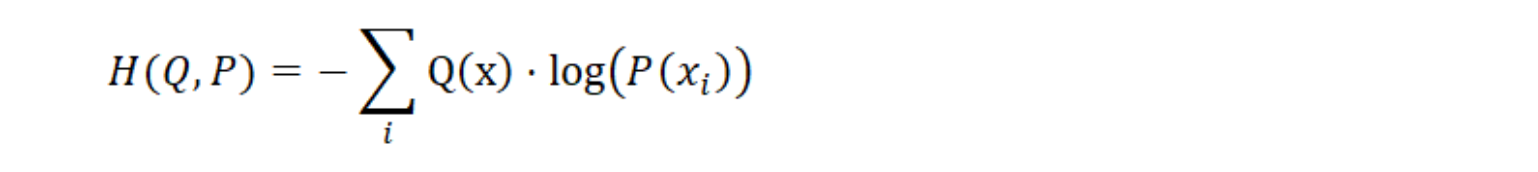
이 단순화 된 버전을 교차 엔트로피 손실(Cross Entropy Loss)이라고 하며 H(Q, P)로 표시한다. 이것은 이 장에서 예측된 Action-value 분포와 목표(경험, empirical) 분포 사이의 오차를 얻기 위해 사용할 실제 손실 함수이다.
Listing 7.8 교차 엔트로피 손실 함수(Cross Entropy Loss function)
def lossfn(x,y):#A
loss = torch.Tensor([0.])
loss.requires grad=True
for i in range(x.shape[0]): #B
loss_ = -1 * torch.log(x[i].flatten(start_dim=0)) @ y[i].flatten(start_dim=0) #C
loss = loss + loss_
return loss
#A 예측 분포`x`와 목표 분포`y` 사이의 손실
#B 배치 차원을 통한 루프
#C 일련의 연결된 분포를 얻기 위해 Action 차원을 따라 편탄화(flatten)
lossfn 함수는 B x 3 x 51 차원의 예측 분포 ‘x’와 동일한 차원의 목표 분포 ‘y’를 취한 다음 Action 차원에 대한 분포를 평탄화하여 B x 153 행렬을 얻는다. 그런 다음 행렬의 각 행 1 x 153 을 반복하여 1 x 153 예측 분포와 1 x 153 대상 분포 사이의 교차 엔트로피를 계산한다. x와y의 곱을 명시적으로 합산하는 대신,이 두 연산을 결합해주는 내적 연산자@를 사용하여 결과를 한 번에 얻을 수 있다.
취해진 Action에 대한 특정 Action-value 분포 사이의 손실을 계산하도록 선택할 수 있지만, Dist-DQN이 다른 두 Action를 변경하지 않고 유지하도록 학습하기 위해 3개의 Action-value 분포에 대한 손실을 계산하고 수행된 Action-value 분포만 업데이트한다.
7.6 시뮬레이션 데이터에 대한 Dist-DQN
Dist-DQN이 목표 분포에 맞게 성공적으로 학습 할 수 있는지 시뮬레이션된 목표 분포를 가지고 지금까지 모든 코드들을 테스트해 보겠다.
Listing 7.9 시뮬레이션 데이터로 테스트
aspace = 3 #A
tot_params = 128*100 + 25*100 + aspace*25*51 #B
theta = torch.randn(tot_params)/10. #C
theta.requires_grad = True
theta_2 = theta.detach().clone() #D
#
vmin,vmax = -10,10
gamma = 0.9
lr = 0.00001
update_rate = 75 #E
support = torch.linspace(-10,10,51)
state = torch.randn(2,128)/10. #F
action_batch = torch.Tensor([0,2]) #G
reward_batch = torch.Tensor([0,10]) #H
losses = []
pred_batch = dist_dqn(state,theta,aspace=aspace) #I
target_dist = get_target_dist(pred_batch,action_batch,reward_batch,\
support, lim=(vmin,vmax),gamma=gamma) #J
plt.plot((target_dist.flatten(start_dim=1)[0].data.numpy()),color='red',label='target ')
plt.plot((pred_batch.flatten(start_dim=1)[0].data.numpy()),color='green',label='pred' )
plt.legend()
#A Action 공간이 3이 되도록 정의
#B 레이어 크기를 기준으로 총 Dist-DQN 파라미터 수 정의
#C Dist-DQN의 파라미터 벡터를 무작위로 초기화
#D Target Network 로 사용할 `theta`복제
#E 75 스텝마다 Dist-DQN의 main 및 target 매개 변수를 동기화
#F 테스트를 위해 두 가지 State를 무작위로 초기화
#G 합성 Action 데이터 작성
#H 합성 Reward 데이터 생성
#I Prediction 배치를 초기화
#J Target 배치 초기화
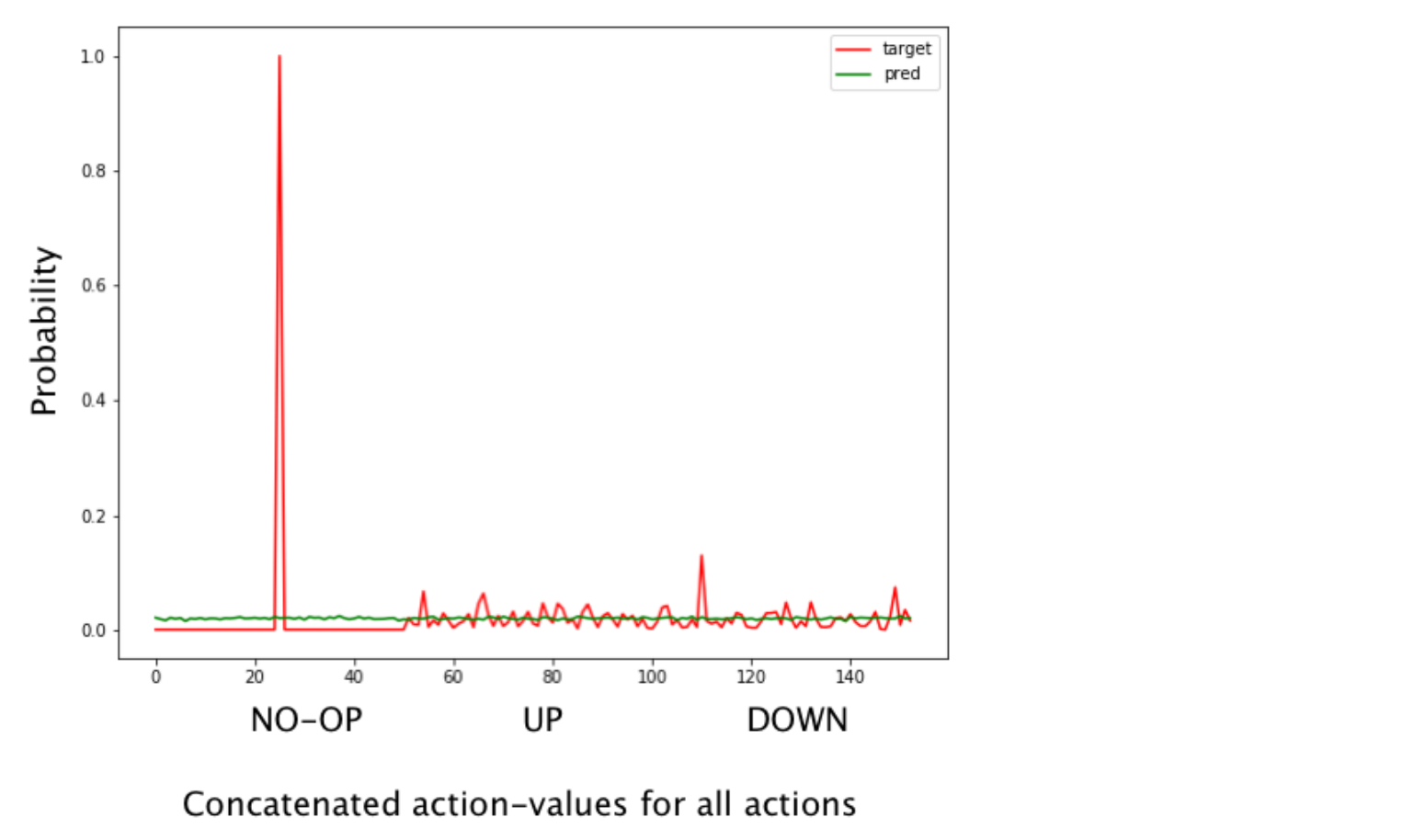
Figure 7.15: 훈련되지 않은 Dist-DQN에 의해 생성된 예측된 Action-value 분포와 Reward을 관찰한 후 목표 분포를 보여준다. 길이가 51-요소 인 3개의 개별 Action-value 분포가 있지만 여기서는 예측과 목적 사이의 전반적인 일치를 보기 위해 하나의 긴 벡터로 연결(concatenate)했다. 첫번째 51개 요소는 ‘NO-OP’ Action의 Action-value 분포에 해당하고, 두번째 51개 요소는 ‘UP’ Action의 Action-value 분포에 해당하고 마지막 51개 요소는 ‘DOWN’ Action의 Action-value 분포에 해당한다. 예측은 3가지 동작 모두에 대해 완전히 평평한(Uniform) 분포인 반면, 목표 분포에는 동작 0에 대한 최빈값(Mode)(즉, Peak, 가장 높히 올라간 값)와 다른 두 Action에 대한 일부 노이즈 피크가 있다. 우리의 목표는 목적 분포와 일치하는 예측을 얻는 것이다.
여기에서는 2개의 샘플 데이터에 대한 분포를 학습 할 수 있는 Dist-DQN 의 기능을 테스트한다. Action 0은 0의 Reward와 관련이 있으며, Action 2는 10의 Reward와 관련이 있다. Dist-DQN은 State 1이 Action 1과 연관되어 있고 State 2가 Action 2와 연관되어 있고 분포를 학습 할 것으로 기대한다. 무작위로 초기화된 모수(Parameter) 벡터를 사용하면 3가지 Action(Action 차원을 따라 평탄화 됨)에 대한 예측 분포가 거의 균일한(Uniform) 분포임을 알 수 있지만 목적 분포는 0에서 피크이다(코드상에서 첫 번째 샘플을 시각화 했음). 학습 후 예측 및 목적 분포는 거의 일치해야 한다.
Target Network가 중요한 이유는 Dist-DQN에서 매우 분명하다. Target Network는 지연 시간(lag time) 후에 업데이트되는 Main 모델의 복사본일 뿐이다. 우리는 학습을 위한 Target을 만들기 위해 Target Network의 예측을 사용하지만 그라디언트 디센트(gradient descent)를 수행하기 위해서는 Main 모델의 파라미터만 사용한다. Target Network는 학습을 안정화시킨다. Target Network가 없으면 그라디언트 디센트(gradient descent) 시에 각 매개 변수 업데이트 후 목적 분포가 변경되지만 그라디언트 디센트(gradient descent)가 목적 분포에 대해보다 정확한 방향으로 매개 변수를 이동 시키려고하기 때문에 Dist-DQN의 예측과 목표 분포 사이의 이러한 순환성(Circularity)의 결과로 목표 분포가 급격히 변할 수 있다.
Target Network 인 매개 변수의 지연된 복사(lagged copy)을 통해 Dist-DQN 예측의 지연된 복사를 사용하여 목적 분포는 모든 Iteration마다 변경하지 않으며 Main Dist-DQN 모델의 지속적인 업데이트의 영향을 즉시 받지 않는다. 이것이 학습을 크게 안정화시킨다. update_rate를 1로 줄이고 학습을 시도하면 목적 분포가 완전히 잘못된 방향으로 진화하는 것을 볼 수 있다. 학습하는 과정을 보자.
Listing 7.10 Dist-DQN 학습
for i in range(1000):
reward_batch = torch.Tensor([0,8]) + torch.randn(2)/10.0 #A
pred_batch = dist_dqn(state,theta,aspace=aspace) #B
pred_batch2 = dist_dqn(state,theta_2,aspace=aspace) #C
target_dist = get_target_dist(pred_batch2,action_batch,reward_batch, \
support, lim=(vmin,vmax),gamma=gamma) #D
loss = lossfn(pred_batch,target_dist.detach()) #E
losses.append(loss.item())
# Gradient Descent
with torch.no_grad():
theta -= lr * theta.grad
theta.requires_grad = True
if i % update rate == 0: #F
theta_2 = theta.detach().clone()
plt.plot((target_dist.flatten(start_dim=1)[0].data.numpy()),color='red',label='target')
plt.plot((pred_batch.flatten(start_dim=1)[0].data.numpy()),color='green',label='pred')
plt.plot(losses)
#A 조금 더 어려워 지도록 Reward에 임의의 노이즈를 추가
#B Dist-DQN의 Main 모델을 사용하여 분포 예측
#C Dist-DQN의 Target Network 을 사용하여 분포 예측 (지연된 매개 변수 사용)
#D Target Network의 분포를 사용하여 학습을 위한 목표 분포를 만든다.
#E 손실 함수에서 Main 모델의 분포 예측을 사용한다.
#F Target Network의 매개 변수를 Main 모델 매개 변수와 동기화
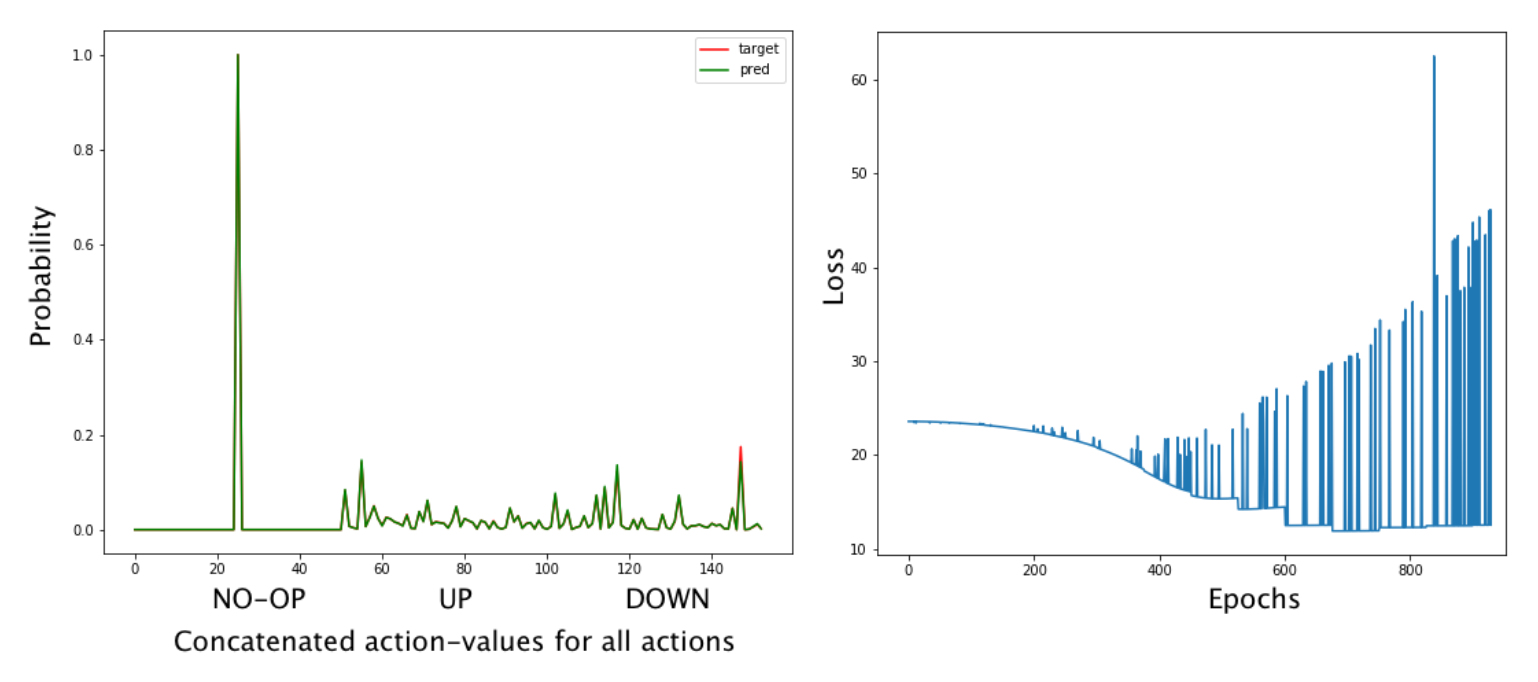
Figure 7.16: 왼쪽 : 학습 후 3가지 Action 모두에 대한 concatenate한 Actoin-value 분포이다. 오른쪽 : 학습 시간에 따른 손실 시각화. Baseline 손실은 감소하고 있지만 점점 증가하는 스파이크(spike)가 있다.
이제 Dist-DQN의 목적과 예측이 학습 후 거의 정확하게 일치함을 알 수 있다(너무 정확해서 두 개의 분포가 겹쳐져 있는 것을 알아채지 못할 수도 있음). 손실 그래프에는 Target Network가 Main 모델과 동기화 될 때마다 급격한 증가가 발생하므로 대상 분포가 갑자기 변경되어 해당 시간 단계에서 정상(normal) 손실보다 높다. 배치의 각 샘플에 대해 각 Action을 학습한 분포를 볼 수 있다 (Listing 7.11).
Listing 7.11 학습된 Action-value 분포 시각화
tpred = pred_batch
cs = ['gray','green','red']
num_batch = 2
labels = ['Action {}'.format(i,) for i in range(aspace)]
fig,ax = plt.subplots(nrows=num_batch,ncols=aspace)
for j in range(num_batch): #A
for i in range(tpred.shape[1]): #B
ax[j,i].bar(support.data.numpy(),tpred[j,i,:].data.numpy(),\
label='Action {}'.format(i),alpha=0.9,color=cs[i])
#A 배치에 있는 경험을 통한 루프
#B 각 Action을 반복
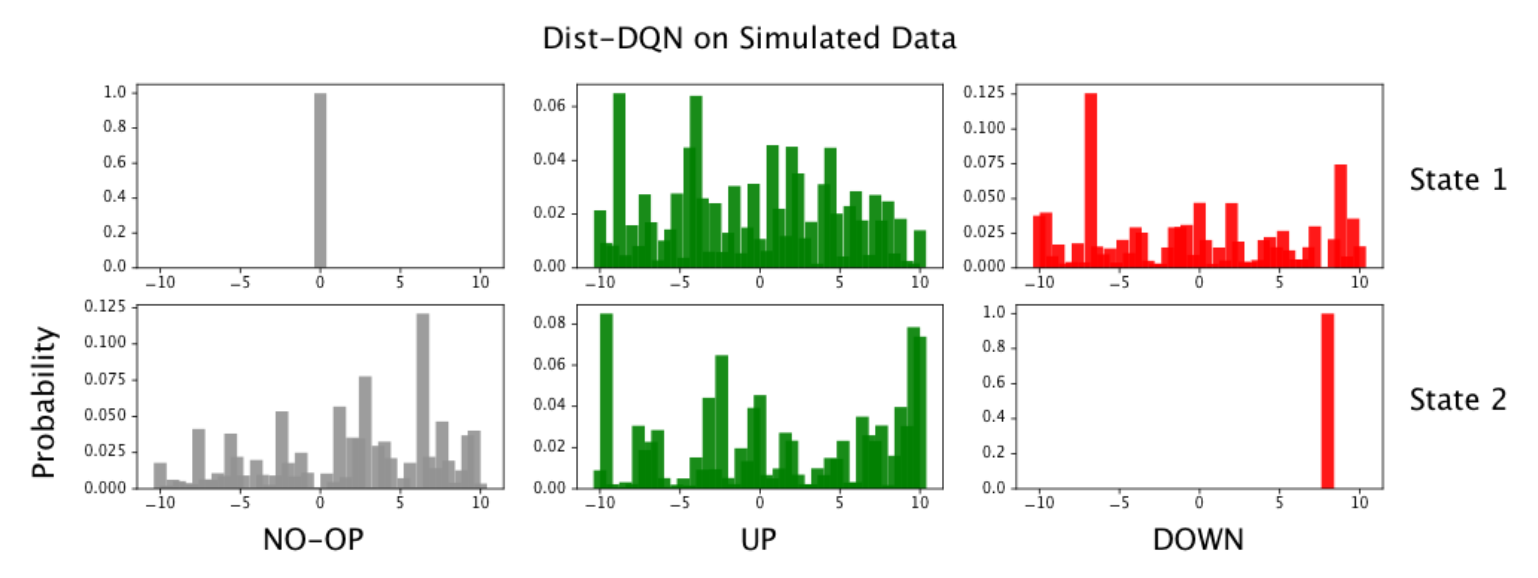
Figure 7.17: 각 행에는 개별 State에 대한 Action-value 분포가 포함되어 있다. 행의 각 열은 각각 Action 0, 1, 2에 대한 분포이다.
첫 번째 샘플에서 Action 0과 관련된 왼쪽의 분포가 시뮬레이션된 데이터와 같이 0에서 퇴화 분포로 축소 된 것을 볼 수 있다. 그러나 다른 두 동작은 명확한 피크없이 매우 균일하게 유지된다. 마찬가지로 배치의 두 번째 샘플에서 Action 2 분포는 데이터가 10 에서 퇴화 분포이며, 다른 두 Action은 매우 균일하게 유지된다.
이 Dist-DQN 테스트 코드에는 Atari Freeway를 사용한 실제 실험에 사용할 거의 모든 개념이 들어 있다. Freeway를 플레이하기 전에 필요한 2 가지 함수가 있습니다. 하나는 OpenAI Gym 환경에서 반환된 State를 전처리하는 것이다. 0에서 255까지의 요소를 가진 128 요소의 numpy 배열을 얻지만 이것을 PyTorch 텐서로 변환하고 그라디언트의 크기를 조정하기 위해 값을 0과 1 사이로 정규화해야 한다.
또한 예측된 Action-value 분포를 고려하여 취할 행동을 결정하는 Policy 함수가 필요하다. Action-value에 대한 완전한 확률 분포를 통해보다 정교한 위험 민감성 정책(Risk-Sensitize Policy)을 활용할 수 있다. 이 장에서는 복잡성을 최소화하기 위해 예상값에 따라 간단한 Action을 선택하는 간단한 Policy을 사용한다. 예를 들어, 우리는 확률 분포를 학습했지만 일반적인 Q-learning 에서와 같이 기대값을 기반으로 Action을 선택한다.
Listing 7.12 State 전처리 및 Action 선택
def preproc_state(state):
p_state = torch.from_numpy(state).unsqueeze(dim=0).float()
p_state = torch.nn.functional.normalize(p_state,dim=1) #A
return p_state
def get action(dist,support):
actions = []
for b in range(dist.shape[0]): #B
expectations = [support @ dist[b,a,:] \
for a in range(dist.shape[1])] #C
action = int(np.argmax(expectations)) #D
actions.append(action)
actions = torch.Tensor(actions).int()
return actions
#A State 값을 0과 1 사이로 정규화
#B 분포의 배치 차원을 통한 루프
#C 각 Action-value 분포에 대한 기대값 계산
#D 기대값이 가장 높은 Action을 계산
서포트 텐서의 내적을 확률 텐서로 간단히 가져와서 이산 분포의 기대값을 계산할 수 있다. 3가지 Action 모두에 대해 이 작업을 수행하고 기대값이 가장 높은 Action을 선택한다. 코드에 익숙해지면 더 복잡한 Policy를 시도해 볼 수 있다. 아마도 각 Action-value 분포의 분산(즉, 신뢰도)을 고려하는 Policy 가 될 것이다.
7.7 Freeway 게임을 하는 Distributional Q-learning
이제 Dist-DQN 알고리즘을 사용하여 Atari 게임 Freeway를 플레이 할 준비가 되었다. 이미 설명한 것 외에 다른 함수는 필요하지 않다. 학습을 안정화시키기 위해 Dist-DQN의 Main 모델과 사본, Target Network를 갖게 될 것이다. Epoch에 따라 엡실론 값이 감소하는 엡실론 탐욕 전략(Epsilon- Greedy Strategy)을 사용할 것이다. 따라서 엡실론 확률에 따라 Action 선택이 임의적(Random)이다. 그렇지 않으면 get_action 함수를 사용하여 가장 높은 기대값을 기반으로 Action을 선택한다. 또한 일반적인 DQN과 마찬가지로 Experience Replay 메커니즘을 사용한다.
가장 기본적인 형태의 Prioritized Replay을 소개한다. 정상적인 Experience Replay에서는 에이전트가 가진 모든 경험을 고정 크기 메모리 버퍼에 저장하고 새로운 경험은 이전 경험을 무작위로 대체한다. 그런 다음 학습을 위해 이 메모리 버퍼에서 배치를 무작위로 샘플링한다. 거의 모든 Action에 대해서 -1 Reward가 발생하고 +10 또는 -10 Reward는 /거의없는 Freeway와 같은 게임에서 Experience Replay 메모리는 기본적으로 동일한 내용을 나타내는 데이터에 의해 크게 지배된다. 이 경우 에이전트에게 유익하지 않으며 게임에서 이기거나 지는 것과 같은 진정으로 중요한 경험은 강하게 희석되어 학습 속도가 크게 느려진다.
이 문제를 완화하기 위해 게임의 승리 또는 패배 상태로 이어지는 Action을 취할 때마다 (예 : -10 또는 +10의 보상을 받는 경우) 이 경험의 여러 사본을 Replay Buffer에 추가하여 많은 -1 Reward 경험으로 부터 희석되는 것을 방지합니다. 따라서, 에이전트가 단순히 게임의 연속만 되는 것이 아닌 성공 또는 실패로 이어지는 것을 에이전트가 학습하기를 원하기 때문에 정보가 적은 다른 경험에 비해 정보가 풍부한 특정 경험을 우선 순위로 둔다.
이 책의 GitHub (https://github.com/DeepReinforcementLearning/DeepReinforcementLearningInAction/)에서 이 장의 코드에 액세스하면 학습 중 라이브 게임 플레이의 화면프레임을 기록하는 데 사용된 코드를 찾을 수 있다. 또한 Action-value 분포의 실시간 변경 사항을 기록하여 게임 플레이가 예측된 분포에 미치는 영향을 확인할 수 있으며 그 반대도 마찬가지이다. 코드를 보여줄 공간이 너무 많이 필요하기 때문에 여기에 해당 코드를 포함시키지 않았다.
Listing 7.13 Distributional Q-learning 로 Freeway 플레이하기 준비
import gym
from collections import deque
env = gym.make('Freeway-ram-v0')
aspace = 3
env.env.get_action_meanings()
vmin,vmax = -10,10
replay_size = 200
batch_size = 50
nsup = 51
dz = (vmax - vmin) / (nsup-1)
support = torch.linspace(vmin,vmax,nsup)
replay = deque(maxlen=replay_size) #A
lr = 0.0001 #B
gamma = 0.1 #C
epochs = 1300
eps = 0.20 #D starting epsilon for epsilon-greedy policy
eps_min = 0.05 #E ending epsilon
priority_level = 5 #F
update_freq = 25 #G
#Initialize DQN parameter vector
tot_params = 128*100 + 25*100 + aspace*25*51 #H
theta = torch.randn(tot_params)/10. #I
theta.requires_grad=True
theta_2 = theta.detach().clone() #J
losses = []
cum_rewards = [] #K
renders = []
state = preproc_state(env.reset())
#A deque 데이터 구조를 사용한 Experience Replay buffer
#B 학습률(Learning Rate)
#C 할인 요소(Discount Factor)
#D Epsilon-Greedy Policy를 위한 시작 엡실론 값
#E 종료 엡실론 값
#F Prioritized-replay; 이 Replay를 함으로써 유익한 경험을 여러 번 복제
#G 25 스텝마다 Target Network 업데이트
#H Dist-DQN의 총 매개 변수 수
#I Dist-DQN에 대한 파라미터를 무작위로 초기화
#J Target Network의 매개 변수 초기화
#K 게임에서 이길 때를 이 목록에 1로 저장합니다.
메인 트레이닝 루프에 도달하기 전에 필요한 모든 설정과 시작 객체들을 보자. 관련된 모든 것들이 시뮬레이션 테스트에서 한 것과 거의 동일하다. 단, Prioritized-replay 설정은 Replay시에 추가해야 할 유익한 정보 경험(예 : 게임에서 이기기)의 사본 수를 제어한다. 우리는 또한 Epsilon-Greedy Policy을 사용하며 초기에 높은 엡실론 값으로 시작한 다음 학습 중에 최소한의 Exploration 양을 유지하기 위해 엡실론 값을 최소값으로 줄인다.
Listing 7.14 Main 학습 루프
from random import shuffle
for i in range(epochs):
pred = dist_dqn(state,theta,aspace=aspace)
if i < replay_size or np.random.rand(1) < eps: #A
action = np.random.randint(aspace)
else:
action = get_action(pred.unsqueeze(dim=0).detach(),support).item()
state2, reward, done, info = env.step(action) #B
state2 = preproc_state(state2)
if reward == 1: cum_rewards.append(1)
reward = 10 if reward == 1 else reward #C
reward = -10 if done else reward #D
reward = -1 if reward == 0 else reward #E
exp = (state,action,reward,state2) #F
replay.append(exp) #G
if reward == 10: #H
for e in range(priority_level):
replay.append(exp)
shuffle(replay)
state = state2
if len(replay) == replay_size: #I
indx = np.random.randint(low=0,high=len(replay),size=batch_size)
exps = [replay[j] for j in indx]
state_batch = torch.stack([ex[0] for ex in exps],dim=1).squeeze()
action_batch = torch.Tensor([ex[1] for ex in exps])
reward_batch = torch.Tensor([ex[2] for ex in exps])
state2_batch = torch.stack([ex[3] for ex in exps],dim=1).squeeze()
pred_batch = dist_dqn(state_batch.detach(),theta,aspace=aspace)
pred2_batch = dist_dqn(state2_batch.detach(),theta_2,aspace=aspace)
target_dist = get_target_dist(pred2_batch,action_batch,reward_batch, \
support, lim=(vmin,vmax),gamma=gamma)
loss = lossfn(pred_batch,target_dist.detach())
losses.append(loss.item())
loss.backward()
with torch.no_grad(): #J
theta -= lr * theta.grad
theta.requires_grad = True
if i % update_freq == 0: #K
theta_2 = theta.detach().clone()
if i > 100 and eps > eps_min: #L
dec = 1./np.log2(i)
dec /= 1e3
eps -= dec
if done: #M
state = preproc_state(env.reset())
done = False
#A Epsilon-Greedy Policy 에 기반한 Action 선택
#B 환경에서 선택된 Action을 취함.
#C 환경이 1의 Reward를 생성하면 Reward를 +10으로 변경 (도로 건너기에 성공했을 경우)
#D 게임이 끝나면 Reward를 -10으로 변경 (시간이 지나도 도로 건너기에 성공하지 않을 경우)
#E 원래 Reward가 0(게임이 계속 진행 중)인 경우 아무 것도 하지 않으면 벌점을 -1로 변경
#F 시작 State, 관찰된 Reward, 취한 Action 및 다음 State의 튜플 형태로 경험(exprience)을 준비 #G 경험(exprience)을 Replay buffer에 추가
#H Reward가 10이면 게임에서 이긴것을 나타내며 이 경험(exprience)을 증폭
#I Replay buffer가 가득 차면 학습을 시작
#J 그라데이션 디센트
#K Target Network의 매개 변수를 Main 모델 매개 변수와 동기화
#L Epoch 수의 함수 형태로 엡실론을 감소
#M 게임이 끝나면 환경을 재설정
위의 모든 코드는 일반적인 DQN에 사용한 코드와 거의 같은 코드이다. 유일한 변경 사항은 단일 Q-value이 아닌 Q-distribution을 처리하고 Prioritized-replay를 사용한다는 것이다. 손실을 시각하ㅗ하면 다음과 같은 결과가 나타난다.
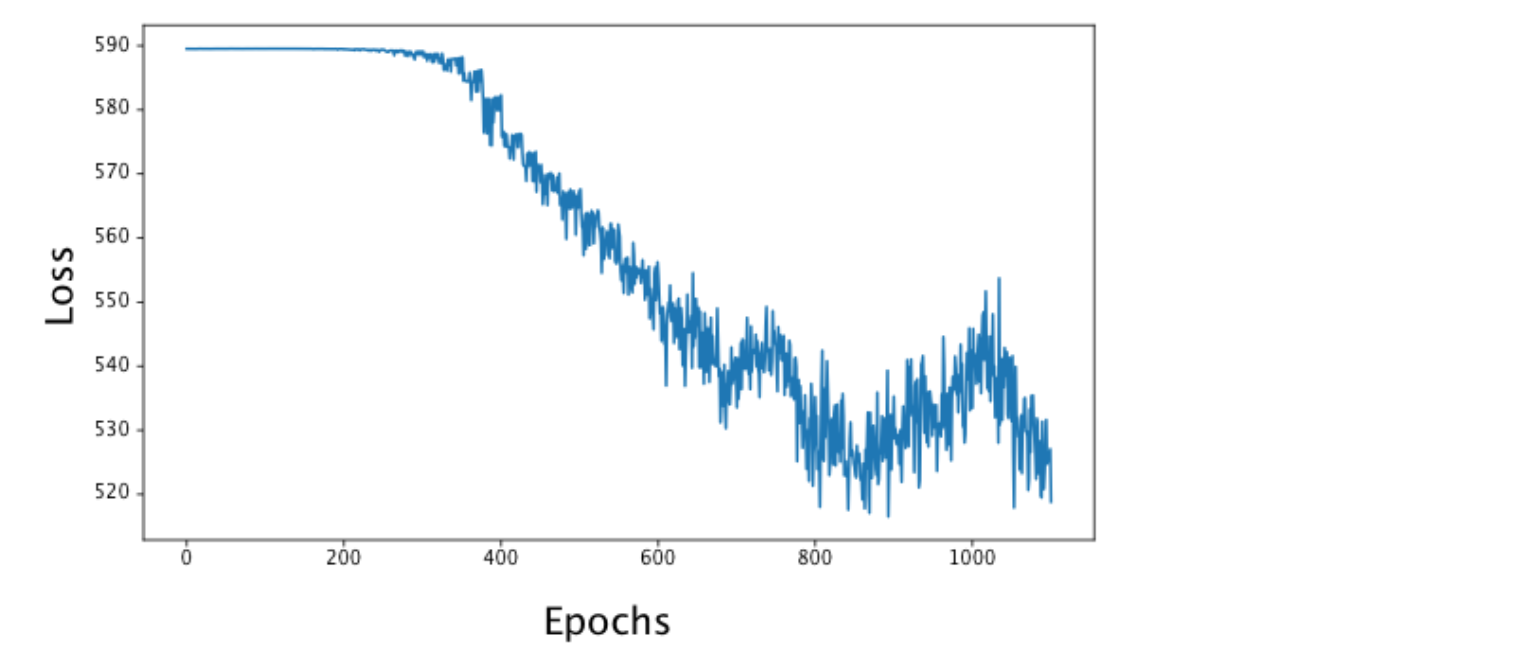
Figure 7.18: Atari 게임 Freeway에서 DIst-DQN 학습을 위한 손실 그래프. 손실은 점차 감소하지만 정기적인 Target Network 업데이트로 인해 “spikiness”가 현저히 보인다.
시뮬레이션 예제에서 보았듯이 Target Network의 업데이트로 인해 일반적으로 손실이 적어지지만 “spikiness”가 있다. cum_rewards 리스트(List)를 조사하면 게임에서 이긴 횟수를 나타내는 [1, 1, 1, 1, 1, 1] 목록이 표시된다. 1이 4개 이상 있다면, 성공적으로 학습을 하고 있는 에이전트을 나타낸다고 볼 수 있다. 또한 예상되는 Action-value 분포와 함께 학습이 진행중인 게임 스크린 샷도 볼 수 있다(GitHub 코드를 참조바람).
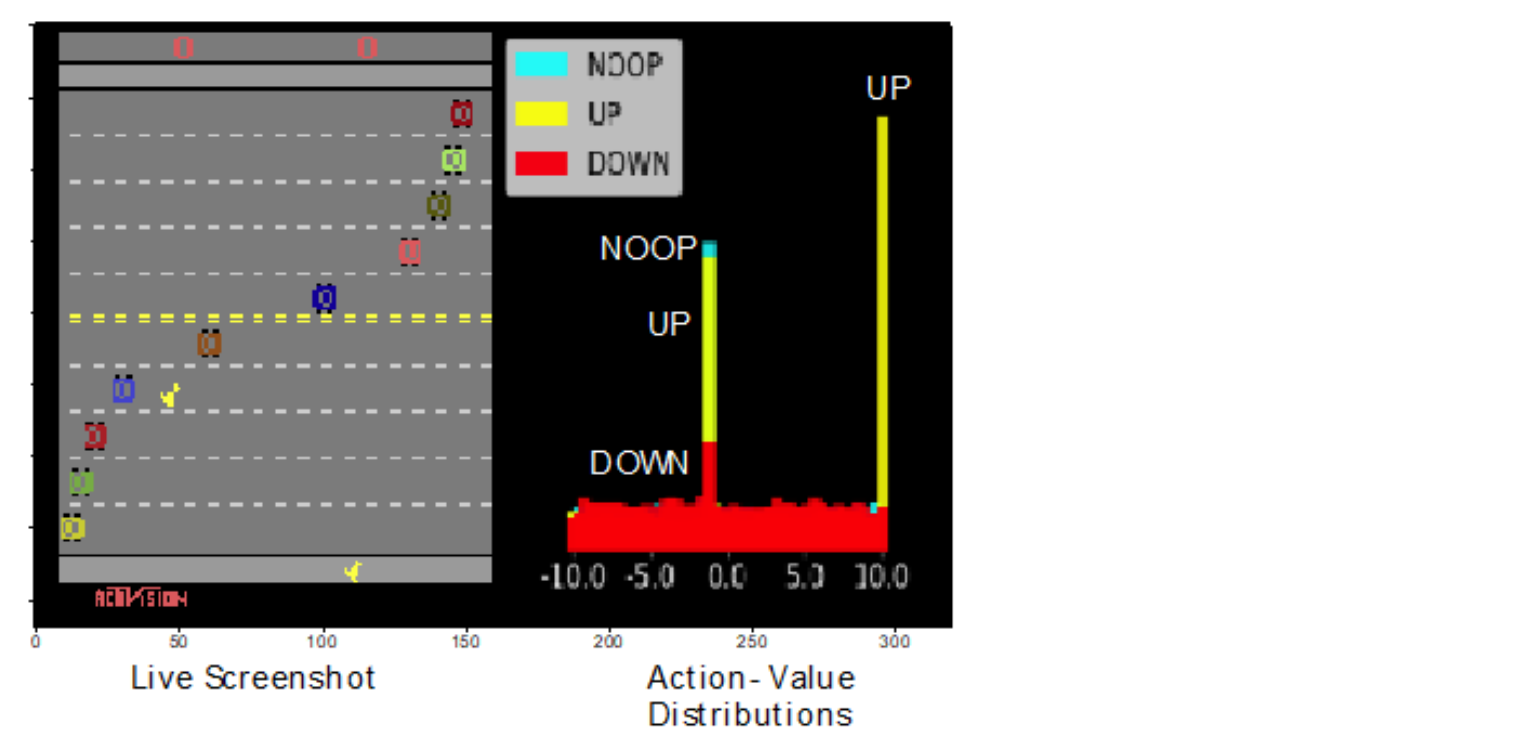
Figure 7.19 : Atari Freeway의 라이브 게임 플레이 스크린 샷. 오른쪽 : 각 Action의 해당 Action-value 분포가 중첩되어 있다. 오른쪽의 스파이크는 Action ‘UP’에 해당하고 왼쪽의 스파이크는 대부분을 차지하고 있는 Action ‘NO-OP’에 해당한다. 오른쪽 스파이크가 더 크므로 에이전트가 UP을 수행 할 가능성이 높아진다.이 경우 오른쪽 Action 이 수행될 것이다. 보기에 어렵지만 ‘UP’ Action에는 왼쪽의 ‘NO-OP’ 스파이크 위에 겹쳐진 스파이크가 있으므로 ‘UP’ Action-value 분포는 bi-modal이므로 ‘UP’ 동작을 수행하면 다음 중 하나가 발생할 수 있다. -1 Reward 또는 +10 Reward 이지만, ‘Up’에 대한 스파이크가 더 높기 때문에 +10 Reward를 받을 확률이 더 높다.
“UP” Action에 대한 Action-value 분포에는 두 가지 모드(최빈값, 피크)가 있다. 하나는 -1에 있고 다른 하나는 +10.0에 있. 이 분포의 기대값이 다른 조치보다 훨씬 높으므로 이 Action이 선택된다. 그리고 Experience Replay buffer로 부터 학습한 분포에서 피크를 치는 모습을 볼 수 있다.
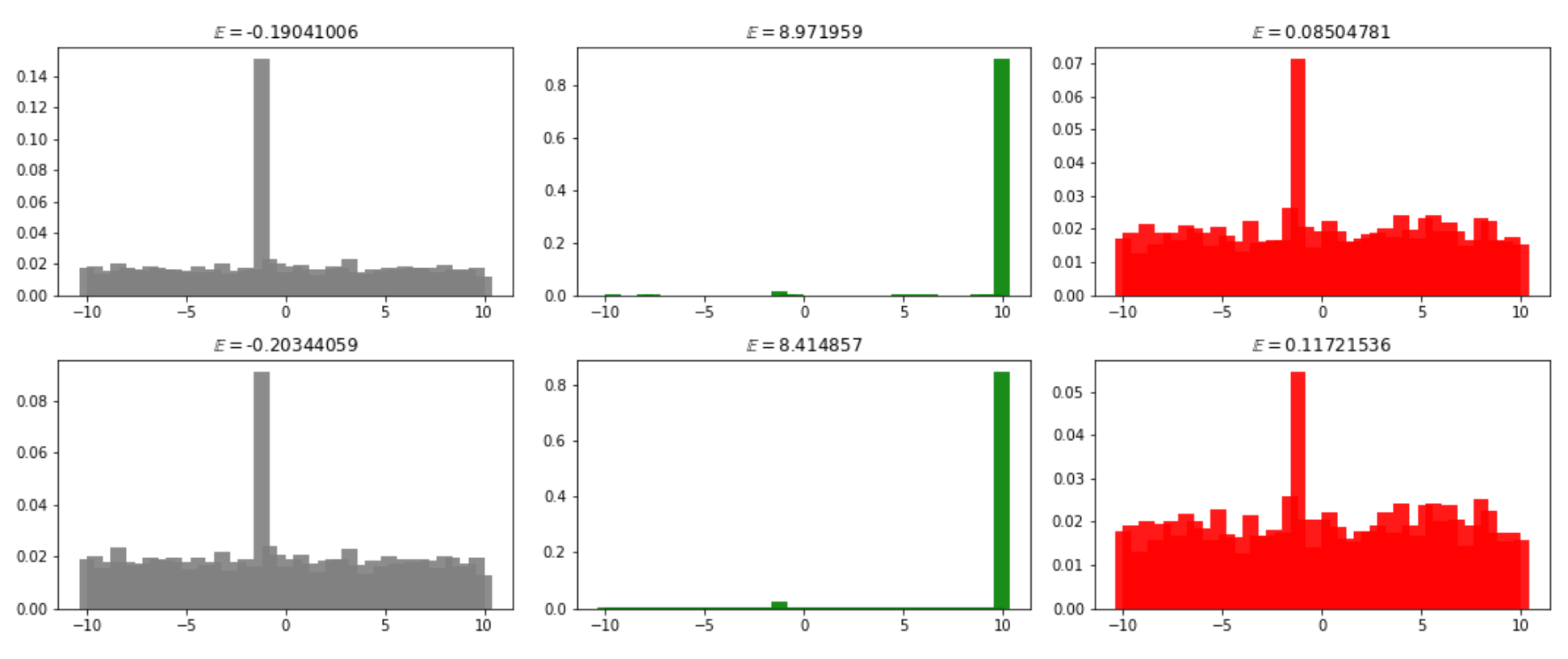
Figure 7.20 : 각 열에는 주어진 State(각 행)에 대한 특정 Action에 대한 Action-value 분포가 있다. 각 그림 위의 숫자는 해당 분포에 대한 가중 평균 값인 해당 분포에 대한 기대값이다. 각 분포는 눈으로 상당히 비슷해 보이지만 기대값은 상당히 다른 동작 선택을 초래할 수 있을 정도로 뚜렷하다.
각 행은 단일 State와 관련된 Replay Buffer의 샘플이다. 행은 각각 “NOOP”, “UP”, “DOWN” Action에 대한 Action-value 분포를 나타낸다. Figure 마다 위에 해당 분포의 기대값이 있다. 모든 샘플에서 “UP” Action의 기대값이 가장 높으며 -1과 +10에 각각 두 개의 명확한 피크가 있음을 알 수 있다. 다른 Action에 대한 분포는 분산이 훨씬 더 크다. 에이전트가 “UP”이 가장 좋은 Action이라는 것을 알게 되면 다른 두 Action을 사용하는 경험이 점점 줄어들어 상대적으로 균일하게 유지되기 때문이다. 더 오랫동안 학습을 계속한다면, 그들은 Epsilon-Greedy Policy 으로 여전히 몇 가지 무작위 Action을 취할 것이기 때문에 결국 -1에서 최고점으로 수렴하고 아마도 -10에서 크기가 작은 또 다른 최고점으로 수렴하게 될 것이다.
앞에서 언급했듯이 Distributional Q-learning은 지난 몇 년 동안 Q-learning에서 가장 크게 개선 된 알고리즘들 중 하나이며 여전히 활발히 연구되고 있다. Dist-DQN을 일반 DQN과 비교해 보고 Dist-DQN으로 전반적인 성능을 향상시켜야 한다. 실제로 Dist-DQN의 성능이 왜 더 나은지 잘 이해하지 못하게 되는 경우가 있는데, 특히 기댓값을 기반으로 작업을 선택하는 경우가 많아서 일수도 있지만 생각해 봐야할 몇 가지 이유가 있다. 하나는 동시에 여러 항목을 예측할 수 있도록 신경망을 훈련시키는 것이 일반화(Generalization)와 전반적인 성능(Overall Perfomance)을 향상시키는 것으로 나타났으며, Dist-DQN은 단일 Action-value가 아닌 3개의 전체 확률 분포를 예측하는 것을 학습하고 있다. 일반적으로 알고리즘이 더 강력한 추상화(Abstraction)를 배우도록 해야 한다.
또한 Dist-DQN을 구현한 방식중에서 중요성 제한(Significance Limitation), 즉 유한한 서포트(Finite Support)로 이산 확률 분포를 사용하고 있으므로 -10에서 10 사이의 매우 작은 범위 내에서만 Action-value를 나타낼 수 있다는 점에 대해서도 논의했다. 물론 더 많은 계산 처리 비용을 투입해서 이 범위를 더 넓게 만들 수 있지만, 이 방법으로는 절대적으로 작거나 큰 값을 표현할 수 없다. 우리가 구현한 방식은 고정된 서포트 집합을 사용하여 관련된 확률의 집합을 학습하는 것이다. 이 문제에 대한 한 가지 해결책은 (학습된)변수 서포트 집합에 대해 고정된 확률 집합을 대신 사용하는 것이다.
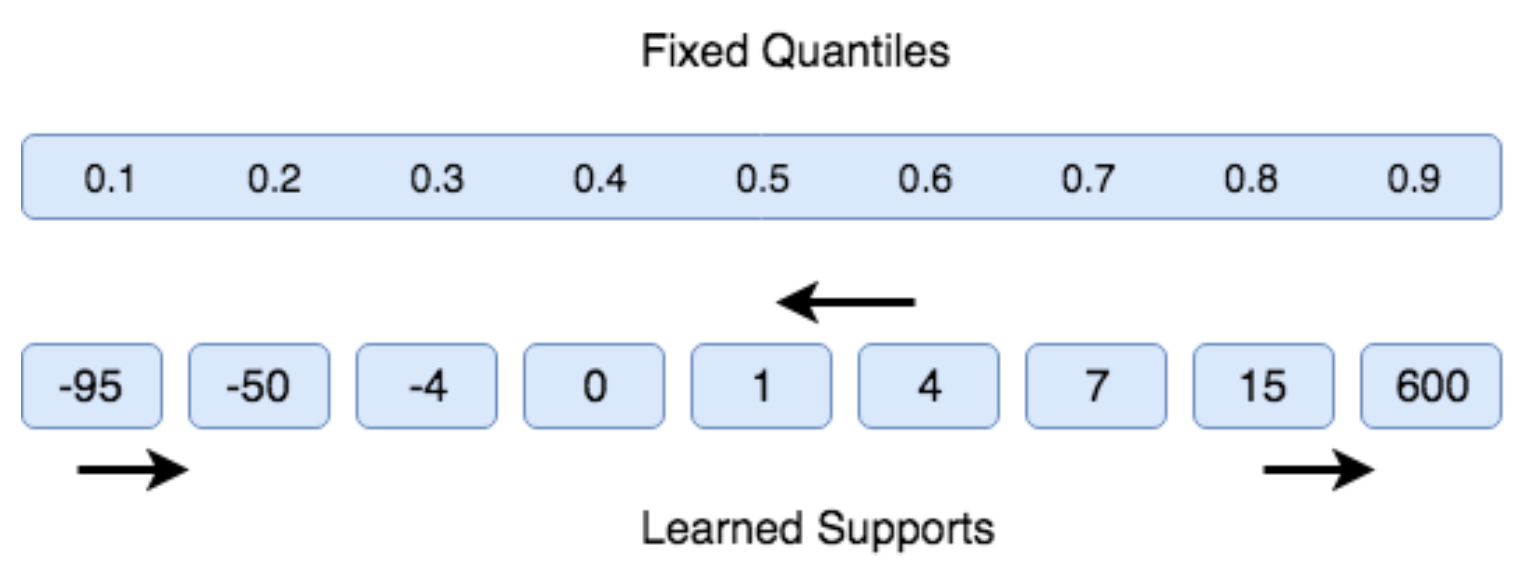
Figure 7.21 : Quantile regression에서 고정 서포트 집합에 할당된 확률을 학습하기보다는 고정 확률 집합 (quantiles)에 해당하는 서포트 집합을 학습한다. 50번째 백분위 수이므로 중앙값이 1임을 알 수 있습니다.
예를 들어, 확률 텐서를 0.1에서 0.9 사이로 고정시킬 수 있다. array ([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]) 대신 Dist-DQN이 고정 확률과 관련된 서포트 집합을 예측하도록 한다. 즉, Dist-DQN이 서포트 값의 확률 0.1, 0.2 등이 무엇인지 학습하도록 하고 있다. 고정된 확률은 분포의 Quantile을 나타 내기 때문에 Quantile Regression이라고 한다. 즉, 50번째 백분위 수 (확률 0.5), 60번째 백분위 수 등에서 서포트를 학습한다. 이 접근 방식을 사용하면 여전히 이산 확률 분포를 가지고 있지만, 가능한 모든 Action-value를 나타낼 수 있다. 즉, 임의로 작거나 클 수 있으며 고정 범위(fixed range)가 없다.
7.8 Summary
- Distributional Q-leaning 의 장점은 성능 향상뿐만 아니라 위험에 민감한 정책을 활용할 수 있는 방법을 제공한다.
- Prioritized-replay은 Experience Replay buffer에서 고도로 유익한 경험의 비율을 높여 학습 속도를 높일 수 있다.
- Bellman 방정식은 Q-function 을 업데이트하는 정밀한 방법을 제공한다.
- OpenAI Gym에는 원시 비디오 프레임이 아닌 RAM State를 생성하는 대체 환경이 포함되어 있다. 이러한 환경은 일반적으로 차원이 훨씬 낮기 때문에 학습하기에 더 쉽다.
- 확률 변수(Random Variable)는 기본 확률 분포(Underlying Probability Distribution)에 의해 가중된 일련의 Outcome(사건)을 취할 수 있는 변수이다.
- 확률 분포의 엔트로피(Entropy)는 포함된 정보의 양을 설명한다.
- KL 발산(KL-divergence)과 교차 엔트로피(Cross-Entropy)는 두 확률 분포 사이의 손실을 측정하는 데 사용할 수 있다.
- 확률 분포의 서포트(Support)는 0이 아닌 확률을 갖는 값의 집합이다. Quantile regression은 확률 집합이 아닌 서포트의 집합을 학습함으로써 매우 유연한 이산 분포를 학습하는 방법이다.

Leave a comment