DRL Curiosity-driven exploration

Chapter 8. Curiosity-driven exploration

(호기심 주도 탐험)

(Orinial Book = ‘Deep Reinforcement Learning in Action’ by Alexander Zai and Brandon Brown)

이 장에서 다룰 내용 :

• 희소 보상 문제(Sparse Reward Problem) 이해
• 호기심(Curiosity)이 본질적 보상(Intrinsic Reward)으로 어떻게 작용할 수 있는지 이해
• OpenAI Gym에서 Super Mario Bros. 플레이
• PyTorch에서 본질적 호기심(Intrinsic Curiosity) 모듈 구현
• DQN 에이전트를 학습시켜 호기심(Curiosity)만으로 Super Mario Bros. 플레이

DQN 및 PG method와 같이 지금까지 연구한 기본 강화 학습 알고리즘은 많은 상황에서 매우 강력한 기술이지만 또 다른 환경에서는 크게 실패한다. Google DeepMind는 Deep Q-learning을 사용하여 에이전트가 초인적 성능(Superhuman Performance) 수준에서 여러 Atari 게임을 하도록 학습하여 2013년 심층 강화 학습(Deep Reinforcement Learning) 분야를 개척했다. 그러나 에이전트의 성능은 여러 유형의 게임에서 매우 다양했다. DeepMind의 DQN 에이전트는 Atari 게임 Breakout(벽돌깨기)에 있어서는 인간의 수준보다 훨씬 더 잘 수행했지만, Montezuma ‘s Revenge(몬테주마의 복수)를 플레이하는 데 있어서는 인간의 수준에 비해서 훨씬 더 나빴다.

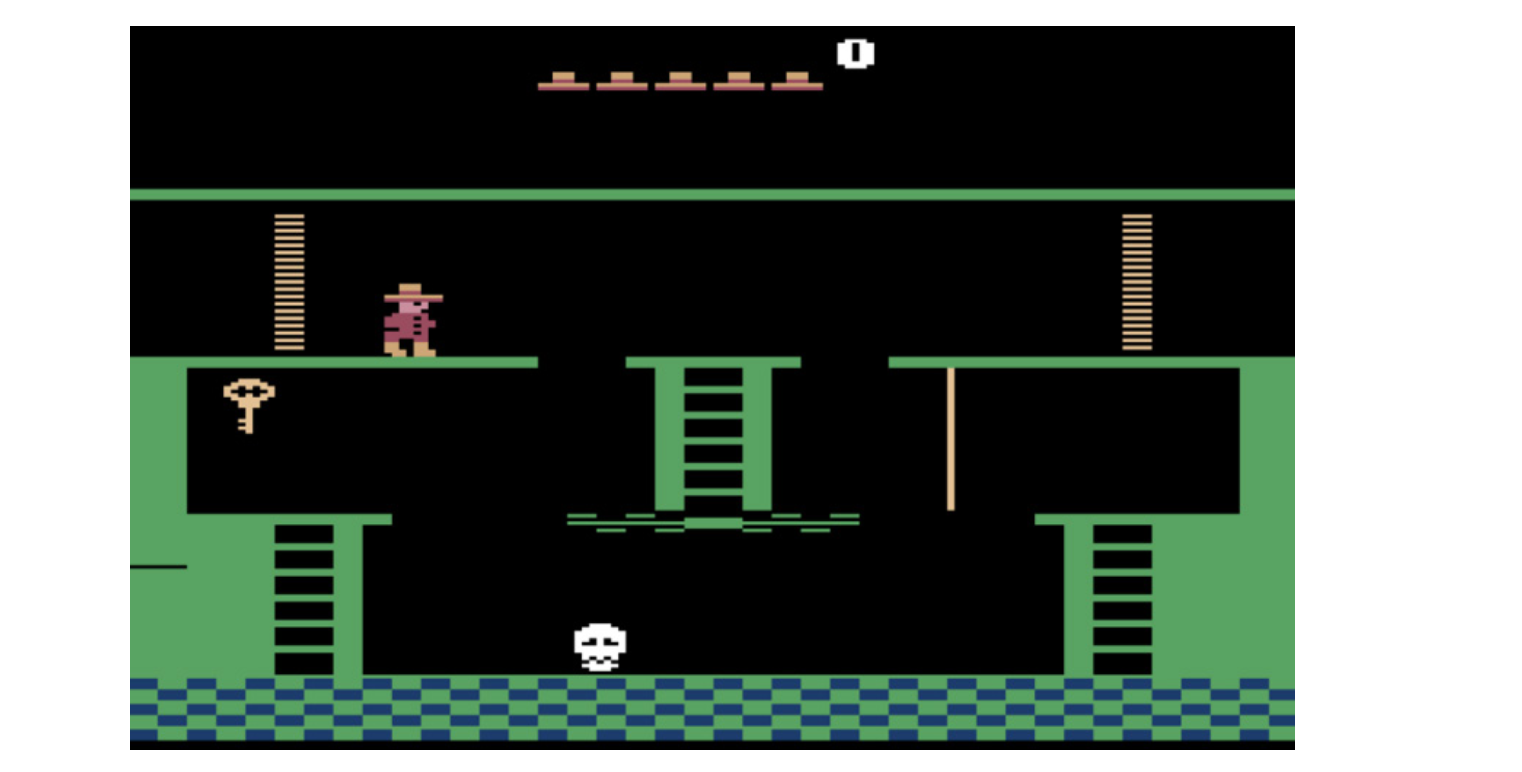
Figure 8.1: Montezuma ‘s Revenge Atari 게임의 스크린 샷. Reward를 받기 위해 열쇠를 얻으려면 먼저 장애물을 탐색해야 한다.

WANT TO LEARN MORE ? 심층 강화 학습 분야에 큰 관심을 받게 된 논문은 2015년 Google DeepMind의 Mnih et al. 이 수행한 “Human-level control through deep reinforcement learning” 이다.이 논문은 읽기 쉽고 결과를 다시 재현할 때 필요한 내용이 매우 자세히 포함되어 있다.

이러한 성능 차이를 만드는 환경의 차이점은 무엇일까? DQN이 성공한 게임은 게임 플레이 중에 비교적 자주 Reward를 받았고 장기적인 계획이 필요하지 않았다. 반면에 몬테 주마의 복수는 방에서 열쇠를 찾은 후에만 Reward를 주는데, 여기에는 수많은 장애물과 적도 포함된다. Vanilla DQN을 사용하면 에이전트가 기본적으로 임의로 탐험을 시작한다. 그것은 임의의 Action을 취하고 Reward를 기다릴 것이며, 그 Reward는 환경에 가장 적합한 행동을 강화시킨다. 그러나 몬테 주마의 복수의 경우, 에이전트가 무작위 탐험 정책(Random Exploration Policy)으로 열쇠를 찾아 Reward를 받을 가능성이 거의 없으므로 Reward에 대한 관찰없고 학습이 되지 않는다.

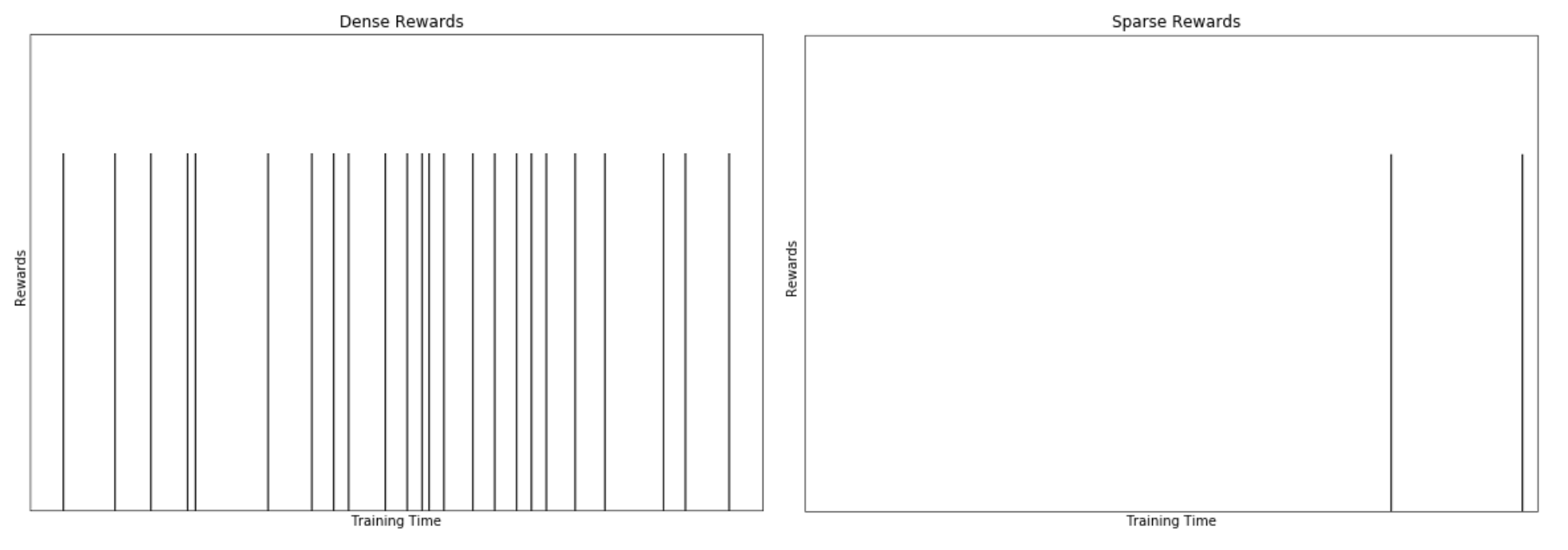
Figure 8.2 : Dense Reward 환경에서는 학습 시간 동안 Reward가 상당히 빈번하게 관찰되어 Action을 쉽게 강화할 수 있다. Sparse Reward 환경에서는 많은 하위 목표(Sub-Goal)가 완료된 후에만 Reward를 받을 수 있어, 에이전트가 Reward만으로 학습하는 것이 어렵거나 불가능하다.

환경의 Reward가 드물게 분포되어 있기 때문에 이 문제를 Sparse Reward Problem 이라고 한다. 에이전트가 자신의 Action을 강화하기에 충분한 Reward를 관찰하지 못하면 학습할 수 없다. 동물과 인간의 학습과정은 인간에게 자연에서 볼수 있는 지능 시스템의 사례를 보여주며, 인간은 이 사례들로 부터 영감을 얻는다. 실제로, 이 Sparse Reward Problem를 해결하려는 연구자들은 인간이 음식과 섹스와 같은 외적(Extrinsic 즉, 외부 환경으로부터) Reward을 극대화 할뿐만 아니라 사물이 어떻게 작동하는지 이해하기 위해 탐험하려는 동기인 본질적 호기심(Intrinsic Curiosity)에 대해서도 실험을 했다.

이 장에서는 인간 지능의 근본 원리, 특히 선천적 호기심을 사용하여 Sparse Reward 환경에서 강화 학습 에이전트를 성공적으로 학습시키는 방법에 대해 공부한다. 호기심이 어떻게 에이전트가 하위 목표를 달성하고 Sparse Reward를 찾는 데 사용할 수 있는 기본 기술의 발전을 이끌 수 있는지 살펴볼 것이다.

8.1 예측 코딩(Predictive Coding)으로 Sparse Rewards 해결하기

신경 과학(Neuroscience), 특히 계산 신경 과학(Computational Neuroscience)의 분야에는 예측 코딩(Predictive Coding) 모델이라고 하는 높은 수준의 신경 시스템을 이해하기 위한 프레임워크가 있다. 이 예측 코딩 모델의 이론은 본질적으로 개별 뉴런부터 대규모 신경망까지 모든 신경 시스템이 입력을 예측하는 알고리즘을 실행하고 있어 예측 오류를 최소화하려고 시도한다고 알려저 있다. 이에 따르면 두뇌가 높은 수준에서 환경으로 부터 많은 감각 정보를 입력받고 감각 정보가 어떻게 관여하는 지 예측하는 학습을 하고 있기 때문에 실제 원시 데이터로 부터 들어오는 데이터로 부터 한 발 더 앞선 예측이 가능하다고 한다.

일상적이지 않은 놀라운 일이 발생하면 (예 : 예기치 않은) 뇌에서 큰 예측 오류가 발생한 후 예기치 않은 상황이 다시 발생하지 않도록 일부 매개 변수 업데이트를 수행한다. 예를 들어, 당신이 방금 만난 사람과 이야기하고 있는 상황을 생각해 보자. 뇌는 방금 만나 사람이 말하기 전에 다음에 할 다음 단어를 예측하려고 노력하고 있을 것이다. 아마도 당신이 모르는 사람이기 때문에 예측시에 뇌는 아마도 평균 예측 오류가 상대적으로 높을 것이다. 그러나 그 사람이 가장 친한 친구라면 문장을 예측하여 완성하는 데 능숙할 것이다. 호기심은 환경의 불확실성을 줄이고(그에 따라 예측 오류를 줄이려는) 일종의 욕구(Desire)라고 생각할 수 있다. 예를 들어, 당신이 소프트웨어 엔지니어이고 머신 러닝이라는 이 흥미로운 분야에 대한 온라인 게시물을 본 적이 있다면 이와 같은 책을 읽는 것에 대한 호기심은 머신 러닝에 대한 불확실성을 줄일 것이다.

예측 오류 메커니즘을 사용하는 것은 호기심을 가진 강화 학습 에이전트에 적용하려는 초기 시도들 중 하나였다. 아이디어는 외적(Intrinsic, 즉, 환경이 제공하는) Reward을 극대화하려고 노력할뿐만 아니라, Action이 주어진 환경의 다음 State를 예측하려고 시도하고 예측 오류를 줄이려고 한다는 것이다. 매우 친숙한 환경에서 에이전트는 작동 방식을 학습하고 예측 오류가 낮다. 이 예측 오류를 다른 종류의 Reward로 사용함으로써 에이전트는 새롭고 알려지지 않은 환경 영역을 방문하도록 장려받는다. 즉, 예측 오류가 높을수록 State가 더 새로운 것이므로 에이전트는 이러한 높은 예측 오류 상태를 방문하도록 인센티브를 받아야 한다. Figure 8.3은 이 접근법의 기본 프레임 워크를 보여준다.

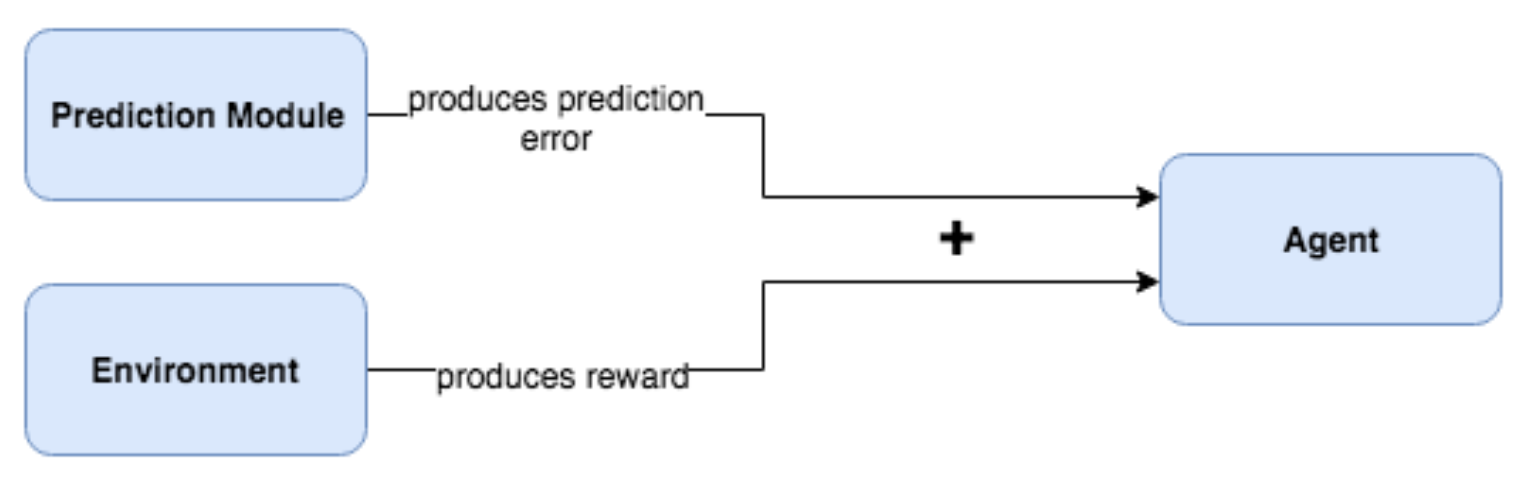
Figure 8.3: 예측 오류는 에이전트가 사용할 외부 환경 Reward와 합산된다.

아이디어는 예측 오차(본질적 보상, Intrinsic Reward 이라고 부를 것임)를 외부 보상(Extrinsic Reward)과 합산하여 이를 환경에 대한 새로운 Reward로 사용하는 것이다. 이제 에이전트는 환경 보상을 극대화하는 방법을 알아낼뿐만 아니라 환경에 대해 호기심을 갖도록 장려받는다. 예측 오차는 Figure 8.4에 따라 계산된다.

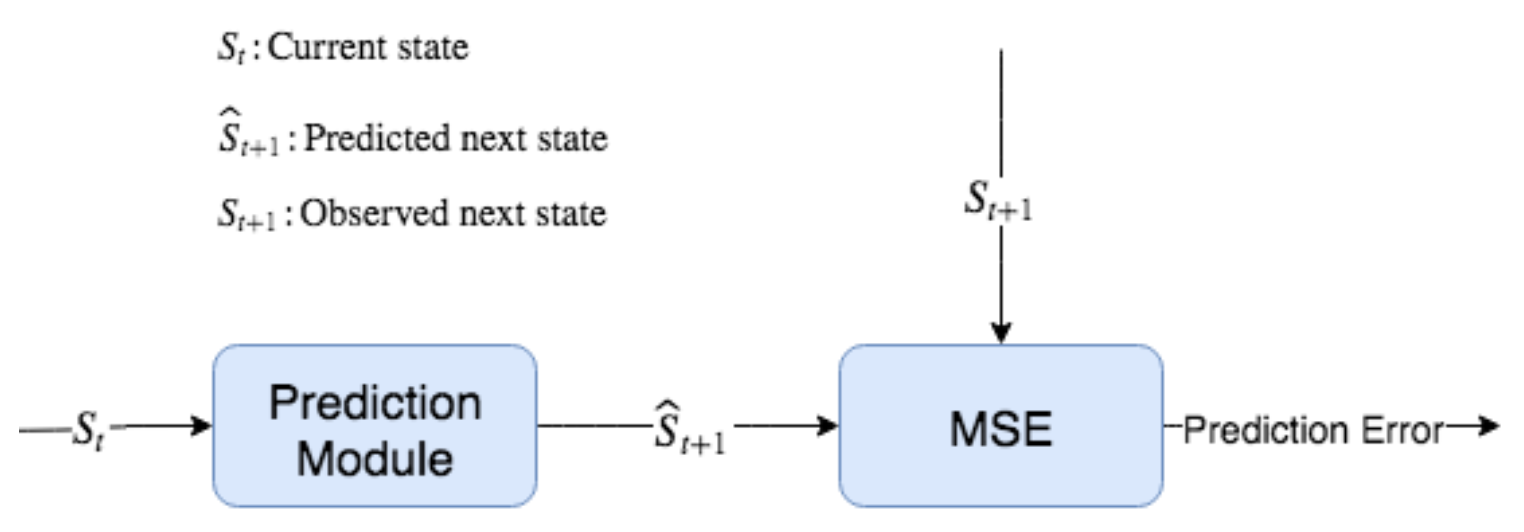
Figure 8.4: 예측 모듈은 State(St)를 취하고 Action(At)을 취하여 다음 State(St + 1)에 대한 예측(S^t+1)을 생성한다. 실제 관측된 다음 State(St + 1)와 함께 이 예측은 예측 에러를 생성하는 평균 제곱 에러(Mean-Squared Error, 또는 다른 에러가 될수도 있음) 함수로 전달된다.

따라서 이 본질적 보상(Intrinsic Reward)은 환경으로 부터 오는 State의 예측 오류를 기반으로 한다. 처음에는 이것이 잘 작동하는 것으로 나타났지만, 이것이 종종 “시끄러운 TV 문제(Noisy TV Problem)”라고 하는 또 다른 문제에 부딪친다는 것을 알게 되었다. 랜덤 노이즈를 재생하는 TV 화면과 같이 일정한 임의의 소스(constant source of randomness)가 있는 환경에서 이러한 에이전트를 학습하면 에이전트는 지속적으로 높은 예측 오류가 발생하여 오류를 줄일 수 없으므로 랜덤 노이즈를 재생하는 TV를 무기한적으로 쳐다볼 수 밖에 없다. 많은 실제 환경에는 이러한 종류의 임의의 소스(예 : 바람에 날리는 나무 잎)가 있기 때문에 이러한 문제는 학문적 문제(Academic Problem)를 넘어선 문제가 된다.

이 시점에서 예측 오류가 많은 잠재력을 가지고 있는 것처럼 보이지만 시끄러운 TV 문제는 큰 결함이라고 봐야 한다. 절대 예측 오차(Absolute Prediction Error)에 주의를 기울이지 말고 예측 오차의 변화율(Rate of Change)에 주의를 기울여야 한다. 에이전트가 예측할 수 없는 State로 전환되면 일시적으로 예측 오류가 발생하지만 사라진다. 마찬가지로 에이전트가 시끄러운 TV 문제를 만나면 처음에는 예측할 수 없으므로 높은 예측 오류가 발생하지만 높은 예측 오류가 계속 유지되므로 변화율은 0이다. 이런 형태는 더 좋지만 여전히 몇 가지 잠재적 인 문제가 있다. 에이전트가 밖에서 바람에 날리는 나뭇잎이 있는 나무를 본다고 상상해 보자. 나뭇잎이 무작위로 바람에 흔들리는 경우 예측 오류가 높다. 바람이 부는 것을 멈추고 나뭇잎이 더 이상 움직이지 않는 경우 예측 오차가 줄어 든다. 그런 다음 바람이 다시 불기 시작하면 예측 오류가 발생한다. 이런 패턴인 경우 예측 오류율(Prediction Error Rate)을 사용하더라도 바람이 부는 것과 함께 변화율이 변동한다. 더 강력한 것이 필요하다.

Figure 8.5: 시끄러운 TV 문제(Noisy TV Problem)는 단순하게 설계된 호기심기반 강화 학습 에이전트가 시끄러운 TV를 통해 학습하지 못한다는 이론적으로 실용적으로 만날 수 있는 문제이다. 이는 예측 불가능성에 의해 Intrinsic Reward를 받게 되고 화이트 노이즈(White Noise)는 예측하기 매우 힘들기 때문이다.

우리는 이 예측 오류 아이디어를 사용하려고 하지만 환경에서 무작위성 또는 예측 불가능성에 취약하지 않기를 바란다. 예측 오류 모듈에 “무관(Doesn’t matter)”제약 조건을 어떻게 추가해야 할까? 문제가 된다고 말할 때, 그것은 우리에게 영향을 미치지 않거나 제어 할 수 없는 것을 의미한다. 바람에 나뭇잎이 무작위로 불면 에이전트의 Action은 나뭇잎에 영향을 미치지 않으며 나뭇잎은 에이전트의 Action에 영향을 미치지 않는다. 이 아이디어는 State 예측 모듈 외에 별도의 모듈로 구현할 수 있으며 이 장의 주제이다. 이 장은 지금까지 논의한 문제를 성공적으로 해결하는 “Curiosity-driven Exploration by Self-supervised Prediction” 논문의 아이디어를 설명하고 이를 구현 한 것을 기반으로 한다.

우리는 이 논문이 Sparse Reward 문제를 해결하는 데 가장 큰 기여를 한 논문중 하나이기 때문에 이 논문을 근접해서 따라가 보기로 한다. 또한 이 분야의 많은 다른 알고리즘들 중에서 가장 쉬운 알고리즘 중 하나이기도 하다. 이 책의 목표 중 하나는 강화 학습의 기초 지식과 기술을 가르치는 것뿐만 아니라 강화 학습 논문을 읽고 이해하고 스스로 구현할 수 있는 충분한 수학 배경을 제공하는 것이다. 물론 일부 논문은 이 책의 범위를 벗어난 고급 수학이 필요하기도 하지만, 강화 학습 분야에서 영향력 있는 논문들을 이해하는 대는 기본 미적분학, 대수학, 선형 대수학에 대한 이해만으로도 충분하다. 따라서 유일한 장벽은 실제로 수학 표기법을 아는 것이다. 물고기를 주는 대신 물고기를 잡는 방법을 알려주고 싶다.

8.2 인버스 역학 예측(Inverse Dynamics Prediction)

예측 모듈 내부를 살펴 보도록 하자. 마지막 섹션의 예측 오류 모듈은 State와 취한 Action를 취하여 예측 된 다음 State를 리턴하는 함수 f : (St, at) → Ŝt + 1로 구현된다. 환경의 역학을 예측하고 있고 미래 상태를 예측하므로 순방향 예측 모델(Forward Prediction Model)이라고 한다.

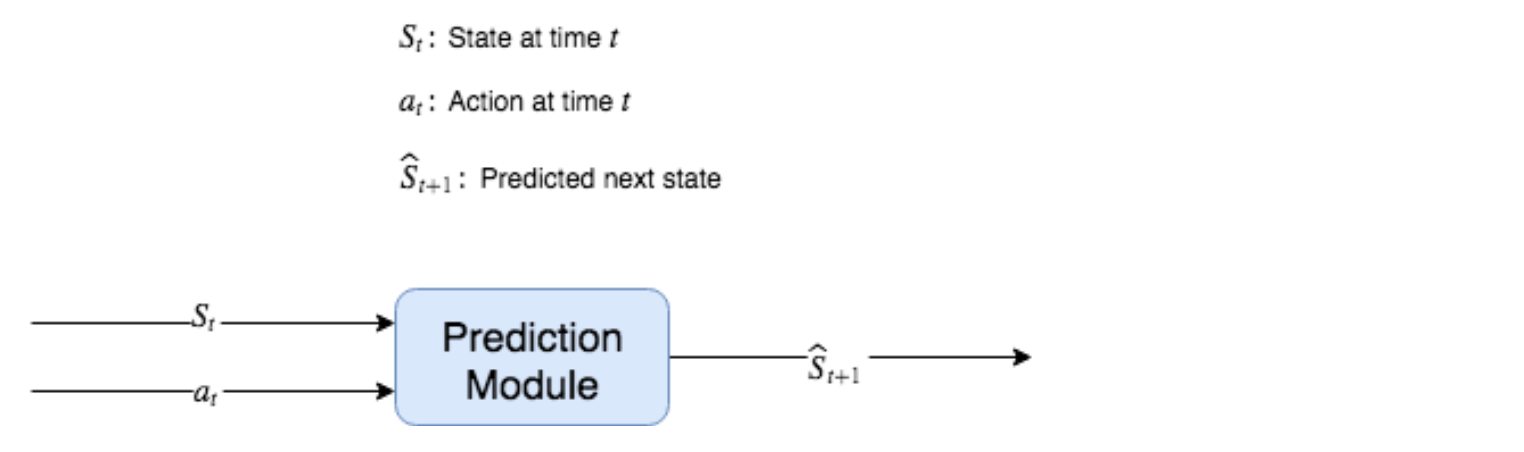
Figure 8.6: 현재 State와 Action을 예측된 다음 State로 매핑하는 순방향 예측 모듈 함수 f : (St, at) → Ŝt + 1의 다이어그램..

우리는 사소하거나 잡음이 많은 부분이 아니라 실제로 중요한 State의 측면만을 예측하고 싶다는 것을 기억하자. 예측 모델에 “무관(Doesn’t matter)”제약 조건을 구축하는 방법은 인버스 모델(Inverse Model) : (St, St + 1) → ât, 즉 State를 취하는 함수 ɡ이다. 다음 State로 전환한 다음 해당 전환이 St에서 St + 1로 이어진 Action을 수행한 예측(A^)을 반환한다.

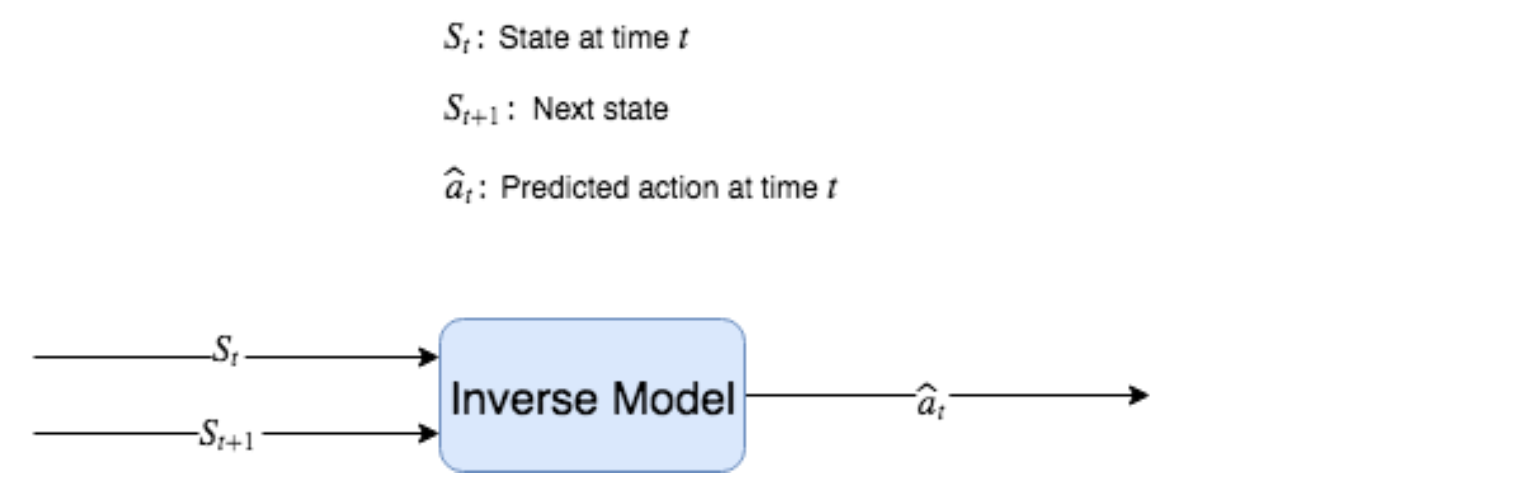
Figure 8.7: 인버스 모델은 두 개의 연속적인 State를 취하고 수행된 Action를 예측하려고 한다.

모델 자체만으로만 본다면 인버스 모델은 실제로 유용하지 않다. 인코더 모델(Encoder Model)이라는 인버스 모델에 밀접하게 결합된 추가 모델이 있다 (이 인코더 모델을 φ 라고 표기한다). 인코더는 φ : St → Ŝt의 함수이다. 즉, 이 함수는 State(St)를 입력으로 받고 인코딩된 State(Ŝt)를 반환한다. 이 때 RAW State인 St보다 현저히 차원이 낮은 인코딩 된 상태 Ŝt를 반환한다. RAW State는 Height, Width, Channel 을 가진 RGB 비디오 프레임을 예로 들 수 있다. φ는 해당 상태를 낮은 차원의 벡터로 인코딩한다. 예를 들어, 총 30,000 개의 요소를 가진 벡터로 100 픽셀 x 100 픽셀 x 3 개의 색상 채널 을 가진 프레임이다. 픽셀들 중 많은 부분이 중복되어 유용하지 않으므로 인코더가 이 State를 High-level 피처를 가진 200 요소 벡터로 인코딩하게 된다.

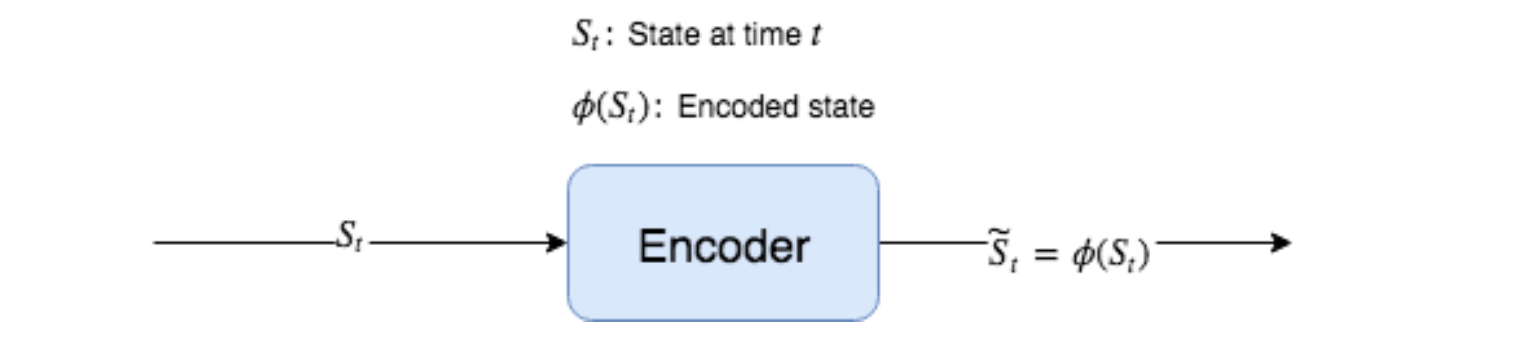
Figure 8.8 : 인코더 모델은 RGB 배열과 같은 고차원 State 표현을 입력받아 저차원 벡터로 인코딩한다.

NOTATION 물결표(~) 기호가 있는 변수는 차원이 다른 기본 변수의 변형된 버전을 나타낸다. 모자(^) 기호가 있는 변수는 기본 State의 근사값(또는 예측)을 나타내며 동일한 차원이다.

엔코더 모델은 인버스 모델을 통해 학습된다. 순방향 및 인버스 모델 f 및 g에 대한 입력으로 RAW State가 아닌 인코딩된 State를 사용하기 때문이다. 즉, 순방향 모델은 함수 f가 된다 f: φ(St) × at → φ^(St+1 ) 여기서 φ^(St + 1)은 인코딩된 State의 예측을 나타내고, 인버스 모델은 함수 ɡ : φ(St ) × φ(St + 1) → (at) 이다.

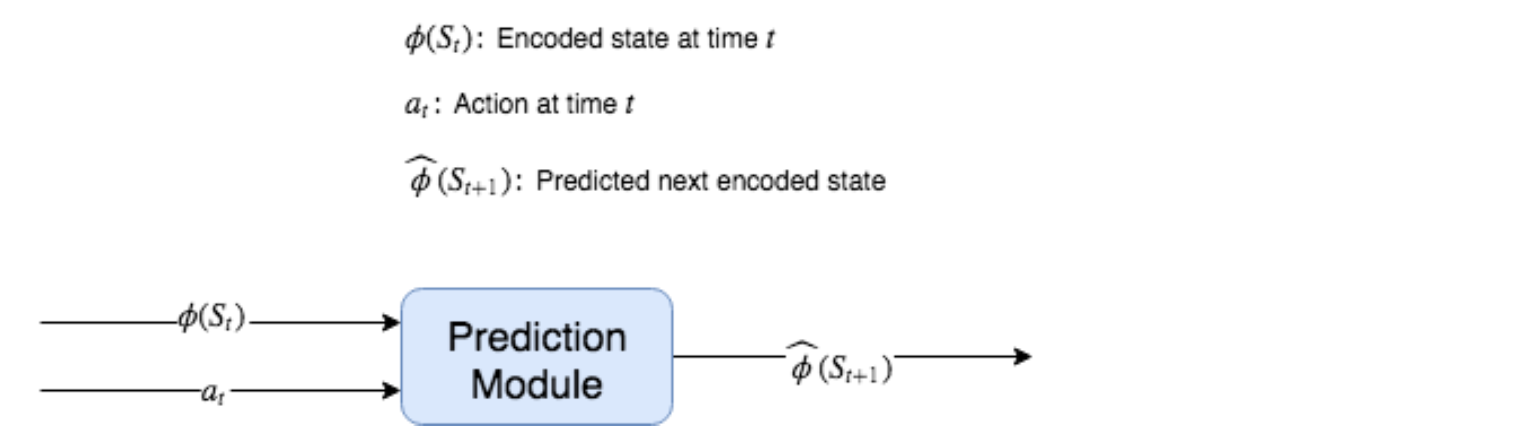
Figure 8.9: 순방향 예측 모듈은 실제로 RAW State가 아닌 인코딩된 State를 사용한다. 인코딩된 상태는 φ(St)로 표시된다.

인코더 모델은 직접 학습되지 않고 Autoencoder가 아니며 인버스 모델을 통해서만 학습된다. 인버스 모델은 인코딩된 상태를 입력으로 사용하여 한 State에서 다음 State로 전환하기 위해 수행된 Action을 예측하려고 시도하며 자체 예측 오류를 최소화하기 위해 오류는 인코더 모델뿐만 아니라 자체로도 역전파(Backpropagation)된다. 그런 다음 인코더 모델은 인버스 모델 작업에 유용한 방식으로 State를 인코딩하는 방법을 학습한다. 순방향 모델은 인코딩된 State를 입력으로 사용하지만 순방향 모델에서 인코더 모델로 역전파되지는 않는다. 만약 그렇다면, 순방향 모델은 모든 State를 단일 고정 출력으로 매핑하도록 인코더 모델을 강제하게 된다. 강제하는 이유는 예측하기 가장 쉬워질 것이기 때문이다. 그림 8.10은 이러한 구성 요소의 전체 그래프 구조를 보여준다.

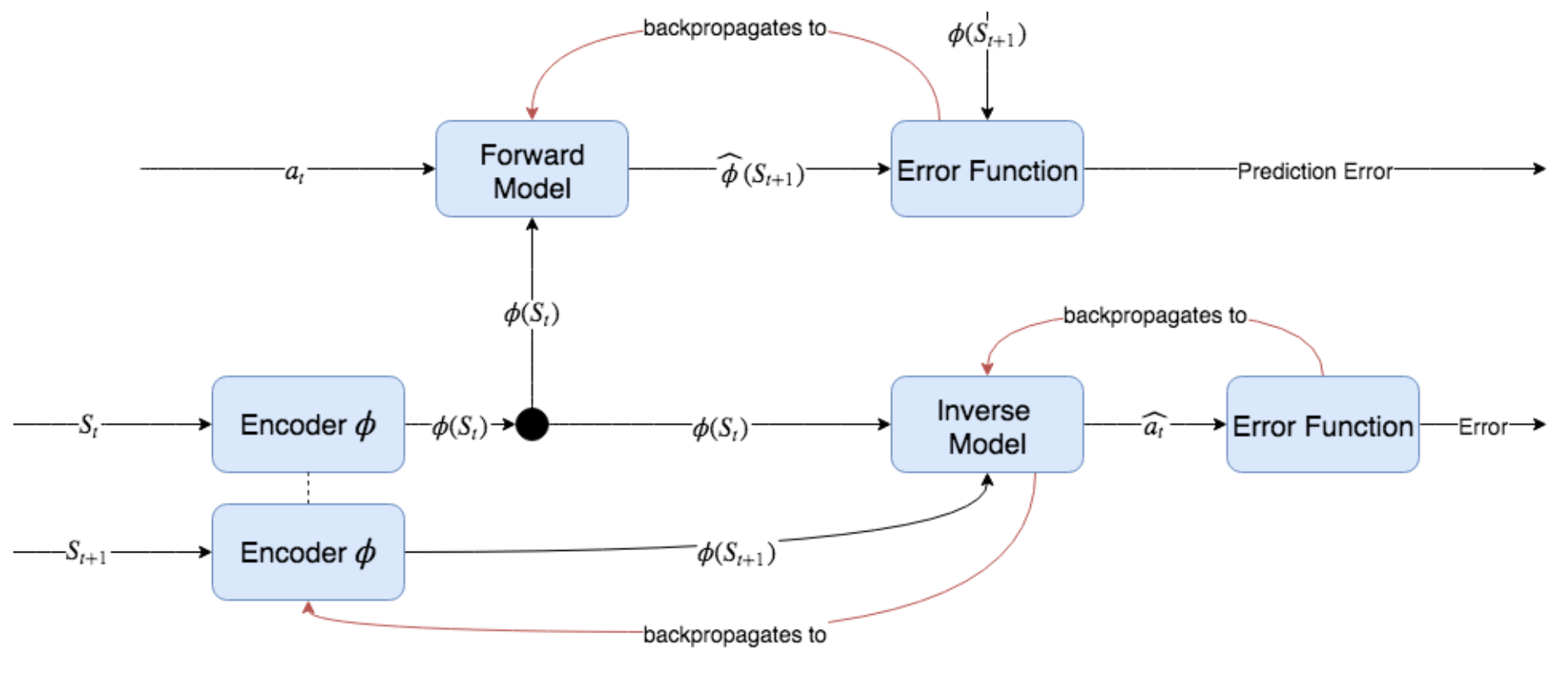
Figure 8.10: 호기심 모듈. 먼저 인코더는 State St 및 St + 1을 각각 저 차원 벡터 φ(St) 및 φ(St + 1)로 인코딩한다. 인코딩된 State는 순방향 및 인버스 모델로 전달된다. 인버스 모델은 인코딩된 모델로 역 전파되어 자체 오류를 통해 학습한다. 순방향 모델은 자체 오류 함수에서 역전파를 통해 학습되지만 인버스 모델과 같이 인코딩된 State로 역전파되지는 않는다. 이를 통해 인코더는 수행된 Action을 예측하는 데만 유용한 State 표현을 생성하는 방법을 학습한다. 검은 색 원은 엔코더의 출력을 복사하고 복사를 순방향 및 인버스 모델로 전달하는 복사 작업을 나타낸다.

Figure 8.10은 이러한 모든 구성 요소의 순방향 패스와 모델 매개 변수를 업데이트하기위한 역방향(역전파) 패스를 보여준다. 인버스 모델은 인코더 모델로 역전파되고 인코더 모델은 인버스 모델과 함께 학습되는 것을 반복한다. 인코더에서 역전파되지 않도록 PyTorch의 detach() 메소드를 사용하여 인코더에서 순방향 모델을 분리해야한다. 엔코더의 목적은 성능 향상을 위해 저차원 입력을 제공하는 것이 아니라 Action 예측과 관련된 정보만 포함한 표현을 사용하여 State를 인코딩하는 방법을 학습하는 것에 있다. 이는 무작위로 변화하고 에이전트의 Action에 영향을 미치지 않는 State의 어떤 측면이 이 인코딩 된 표현에서 제거됨을 의미한다. 이론적으로 이러한 메카니즘이 시끄러운 TV 문제(Noisy TV Problem)를 피하게 해 준다.

순방향 모델과 인버스 모델의 경우 입력 State 데이터 전체 전환을 위해 데이터에 액세스해야 한다. 즉, (St, At, … , St + 1) 전체가 필요하다. 하지만 Deep Q-learning 장에서 사용한 Experience Replay를 사용할 때는 이런 문제가 없다. Replay Buffer 라는 메모리에 이런 종류의 튜플을 저장하기 때문이다.

8.3 슈퍼 마리오(Super Mario Bros.) 게임 설정

순방향, 인버스 및 인코더 모델이 함께 내부 호기심 모듈 (ICM, Internal Curiosity Module)을 형성하며 이 장의 뒷부분에서 자세히 다룰 것이다. ICM의 구성 요소는 에이전트의 호기심을 유발하는 본질적 보상(Intrinsic Reward)을 생성하기 위한 목적으로만 함께 작동한다. ICM은 환경 정보를 기반으로 새로운 본질적 보상(Intrinsic Reward)만 생성하므로 에이전트 모델이 구현되는 방식과 무관하다. A3C(5 장에서 다루는 Actor-Critic Policy Gradient 방법) 모델과 같이 원하는 에이전트 모델 구현을 사용할 수 있지만 여기서는 Q-learning 모델을 사용하여 작업을 단순하게 유지하고 ICM 구현에 집중한다 . ICM은 모든 유형의 환경에 사용할 수 있지만 Sparse Reward 환경에 가장 유용하다. Super Mario Bros.를 테스트 베드로 사용한다.

Super Mario Bros.는 Sparse Reward 문제가 그렇게 심각하지는 않다. 우리가 사용할 특정 환경 구현은 게임을 통한 진행 상황에 따라 부분적으로 보상을 제공하므로 Positive Reward가 거의 지속적으로 제공된다. 그러나 Super Mario Bros.는 외부(Extrinsic, 환경이 제공하는) Reward “끄기”를 선택하여 에이전트가 호기심에 따라 환경을 얼마나 잘 탐험하는지 확인할 수 있기 때문에 여전히 ICM을 테스트하기 위한 훌륭한 환경이다. Super Mario Bros.의 구현에는 NO-OP (no-operation, 즉 아무 것도하지 않음) Action을 포함하여 각 단계마다 수행 할 수 있는 12개의 개별 Action이 있다. 전체 Action 리스트는 다음과 같다.

Table 8.1: Actions in Super Mario Bros.

A = jump, B = run

pip로 Super Mario Bros.를 설치할 수 있다 :

>>> pip install gym-super-mario-bros

설치 한 후 임의의 에이전트를 실행하여 (임의의 Action 수행) 환경을 테스트 할 수 있다 (예 : Jupyter Notebook에서이 코드 실행). 이 장의 모든 코드는 이 책의 GitHub 저장소에 있다. https://github.com/DeepReinforcementLearning/DeepReinforcementLearningInAction/

OpenAI Gym 사용 방법을 다시 보려면 4장을 참조바란다.

Listing 8.1 슈퍼 마리오 환경 설정

import gym
from nes_py.wrappers import JoypadSpace #A
import gym_super_mario_bros
from gym_super_mario_bros.actions import SIMPLE_MOVEMENT, COMPLEX_MOVEMENT #B
env = gym_super_mario_bros.make('SuperMarioBros-v0')
env = JoypadSpace(env, COMPLEX_MOVEMENT) #C

done = True
for step in range(2500): #D
    if done:
        state = env.reset()
    state, reward, done, info = env.step(env.action_space.sample())
    env.render()
env.close()


#A Action을 결합하여 Action 공간을 더 작게 만드는 래퍼 모듈이다.
#B 가져올 수있는 Action 공간에는 5가지 단순 Action과 12가지 복잡 Action이 있다.
#C 환경의 Action 공간을 12 개의 Discrete Action으로 줄인다.
#D 임의의 Action을 취하여 환경을 테스트한다.

환경은 env라는 클래스 객체로 인스턴스화되고 사용해야 할 주요 메소드는 step (…) 메소드입니다. step 메소드는 수행 할 Action를 나타내는 정수를 사용한다. 모든 OpenAI Gym 환경과 마찬가지로 각 Action이 수행 된 후 state, reward, done 및 info 데이터를 반환한다. State는 RGB 비디오 프레임을 나타내는 크기 (240, 256, 3)를 가진 numpy 배열이다. Reward는 -15와 15 사이이며 Forward Process 정도에 따라 결정된다. done 변수는 게임이 끝났는지 여부를 나타내는 부울이다 (예 : Mario가 죽는 경우). info 변수는 다음 메타 데이터가 포함된 파이썬 dictionary 객체이다.

Table 8.2: info 변수 설명 - 각 Action 후에 반환된 메타 데이터

Source: https://github.com/Kautenja/gym-super-mario-bros

x_pos 키 / 값만 사용하면 된다. step 메소드를 호출한 후 state를 얻는 것 외에도 env.render(“rgb_array”)를 호출하여 언제든지 State를 검색 할 수 있다. 이것이 에이전트를 학습시키기 위해서 기본적으로 환경에 대해 알아야 할 모든 것이다.

8.4 전처리 및 Q-Network

전처리를 하지 않은 State는 크기 (240, 256, 3)를 가진 RGB 비디오 프레임으로, 불필요하게 높은 차원이며 이득없이 계산 비용이 많이 든다. 이러한 RGB 상태를 그레이 스케일로 변환하고 크기를 42 x 42로 조정한다.

Listing 8.2 : State 다운샘플링 및 그레이 스케일로 변환

import matplotlib.pyplot as plt
from skimage.transform import resize #A
import numpy as np

def downscale_obs(obs, new_size=(42,42), to_gray=True):
    if to_gray:
        return resize(obs, new_size, anti_aliasing=True).max(axis=2) #B
    else:
        return resize(obs, new_size, anti_aliasing=True)


#A scikit-image 라이브러리에는 이미지 크기 조정 기능이 내장되어 있다.
#B 그레이 스케일로 변환하기 위해 단순히 채널 차원에서 최대값을 가져 와서 대비를 높힌다.

이 함수는 State 배열(obs), 높이와 너비의 새로운 크기를 나타내는 튜플 및 회색조로 변환할지 여부에 대한 부울을 허용한다. 그레이 스케일을 테스트하기 위해 기본적으로 True로 설정한다. scikit-image 라이브러리의 크기 조정 기능을 사용하므로 https://scikit-image.org/download의 지침에 따라 아직 설치하지 않은 경우 설치해야 할 수도 있다. 다차원 배열 형태의 이미지 데이터 작업에 매우 유용한 라이브러리이다.

matplotlib을 사용하여 State의 프레임을 시각화 할 수 있다.

>>> plt.imshow(env.render("rgb_array"))
>>> plt.imshow(downscale_obs(env.render("rgb_array")))

다운샘플링된 이미지는 매우 흐릿하게 보이지만 여전히 게임을 하기에 충분한 시각적 정보가 포함되어 있다.

이러한 RAW State를 유용한 형식으로 변환하기 위해 수행할 다른 데이터 처리 기능이 몇 가지 있다. 우리는 모델에 단일 42x42 프레임을 전달할뿐만 아니라 게임의 마지막 3 프레임 (채널 차원 추가)을 전달하므로 상태는 3x42x42가됩니다. 마지막 3 개의 프레임을 사용하면 모델이 위치 정보가 아닌 속도 정보 (즉, 물체가 얼마나 빠르고 어떤 방향으로 움직이는 지)에 액세스 할 수 있다.

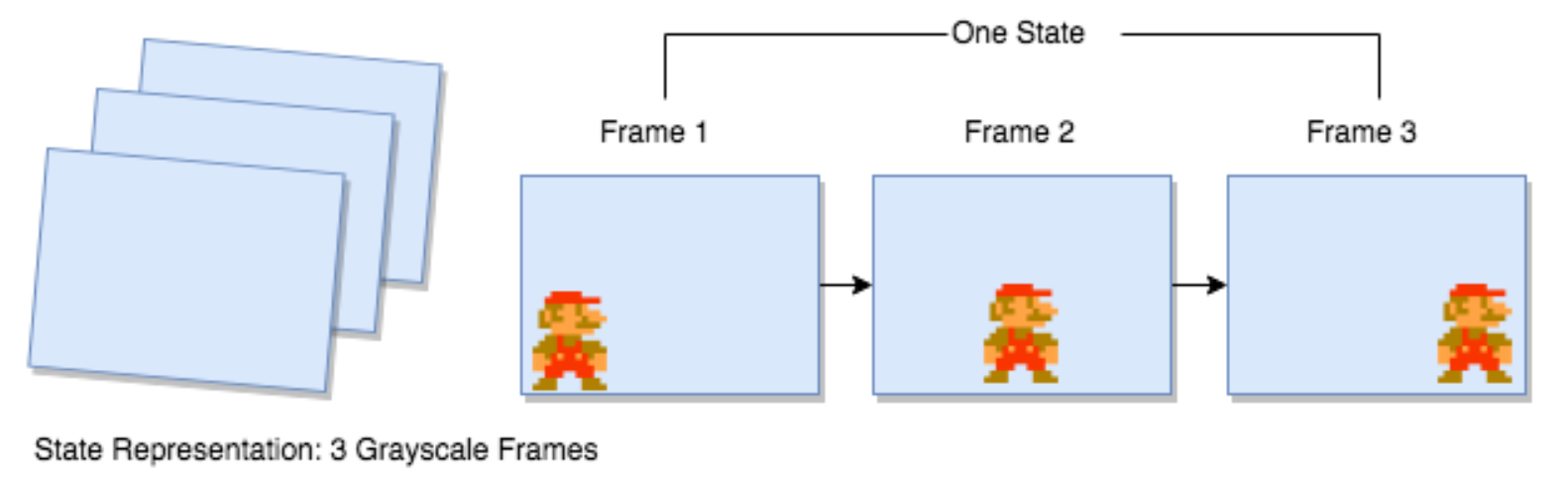
Figure 8.11: 에이전트에게 주어진 각 State는 게임에서 가장 최근 프레임 (회색조) 3개를 연결 한 것이다. 이것은 모델이 물체의 위치뿐만 아니라 이동 방향에도 접근 할 수 있도록 하기 위해 필요하다.

게임이 처음 시작되면 첫 번째 프레임에만 액세스할 수 있으므로 동일한 프레임를 3번 연결하여 3x42x42 State를 얻음으로써 초기 State를 준비합니다. 이 최초 프레임이 복사된 State 후에는 상태의 마지막 프레임을 환경에서 가장 최근의 프레임으로 바꾸고 두 번째 프레임을 이전 마지막 프레임으로 바꾸고 첫 번째 프레임을 이전 초로 바꿉니다. 기본적으로 우리는 고정 길이의 선입 선출 데이터 구조를 가지고 있으며 오른쪽에 추가하면 왼쪽이 자동으로 튀어 나옵니다. Python에는 maxlen 속성이 3으로 설정된 경우이 동작을 구현할 수있는 collection 라이브러리의 deque라는 내장 데이터 구조가 있다.

아래 함수들은 에이전트와 인코더 모델이 사용할 함수로 RAW State를 준비하는 데 사용할 세 가지 함수이다. prepare_state 함수는 이미지 크기를 조정하고, 회색조로 변환하고, numpy에서 PyTorch Tensor로 변환하고 .unsqueeze (dim =) 메서드를 사용하여 배치 차원을 추가한다. prepare_multi_state는 Batch x Channel x Height x Width 차원의 텐서를 가져 와서 새 프레임으로 채널 차원을 업데이트합니다. 이 기능은 훈련된 모델을 테스트하는 동안에 만 사용되며 훈련하는 동안 deque 데이터 구조를 사용하여 프레임을 지속적으로 추가(append)하고 팝(pop)합니다.

Listing 8.4 : State 준비하기

import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
from collections import deque

def prepare_state(state): #A
    return torch.from_numpy(downscale_obs(state, to_gray=True)).float().unsqueeze(dim=0)

def prepare_multi_state(state1, state2): #B
    state1 = state1.clone()
    tmp = torch.from_numpy(downscale_obs(state2, to_gray=True)).float()
    state1[0][0] = state1[0][1]
    state1[0][1] = state1[0][2]
    state1[0][2] = tmp
    return state1

def prepare_initial_state(state,N=3): #C
    state_ = torch.from_numpy(downscale_obs(state, to_gray=True)).float()
    tmp = state_.repeat((N,1,1))
    return tmp.unsqueeze(dim=0)


#A State 다운스케일 및 그레이 스케일로 변환한 다음 PyTorch Tensor로 변환하고 배치 차원을 추가한다.
#B 기존 3프레임 state1 및 새 단일 프레임 2가 주어졌을 때, 최신 프레임을 대기열에 추가한다.
#C 동일한 프레암 사본 3개로 State를 만들고 배치 차원을 추가한다.

8.5 Q-network 과 Policy Function 설정

앞에서 언급했듯이 에이전트로 DQN (Deep Q-network)을 사용한다. DQN은 State를 취하고 Action-value, 즉 각각의 가능한 Action을 취하는 것에 대한 Expected Reward에 대한 예측을 생성한다는 것을 상기하자. 이러한 Action-value을 사용하여 어던 Action을 선택할 것인지에 대한 Policy를 결정한다. 이 게임에는 12개의 개별 Action이 있으므로 DQN의 출력 레이어는 길이가 12인 벡터를 생성한다. 여기서 첫 번째 요소는 Action 0을 취했을 때의 예측되는 값이다.

Action-value는 일반적으로 어느 방향으로든 제한이 없으며, Reward가 Positive이거나 Negative이면 Action-value가 Positive이거나 Negative일 수 있으므로 마지막 레이어에 활성화 함수(Activation function)을 적용하지 않는다 . DQN에 대한 입력은 Batch x 3 x 42 x 42 모양의 텐서이며, 여기서 채널 크기(3)는 가장 최근 3개 프레임의 게임 플레이를 위한 것이다.

DQN의 경우 4개의 컨볼루션 레이어와 2개의 선형 레이어로 구성된 아키텍처를 사용한다. 지수 선형 단위 (ELU, Exponential Linear Unit) 활성화 함수는 각 컨볼루션 레이어와 첫 번째 선형 레이어 다음에 사용된다(마지막 선형 레이어 이후에는 활성화 한수가 없음). 아키텍처는 그림 8.4에 다이어그램으로 표시되어 있다. 실습에서는 에이전트가 long-term temporal 패턴을 학습 할 수있는 LSTM 또는 GRU 계층을 추가 할 수 있다.

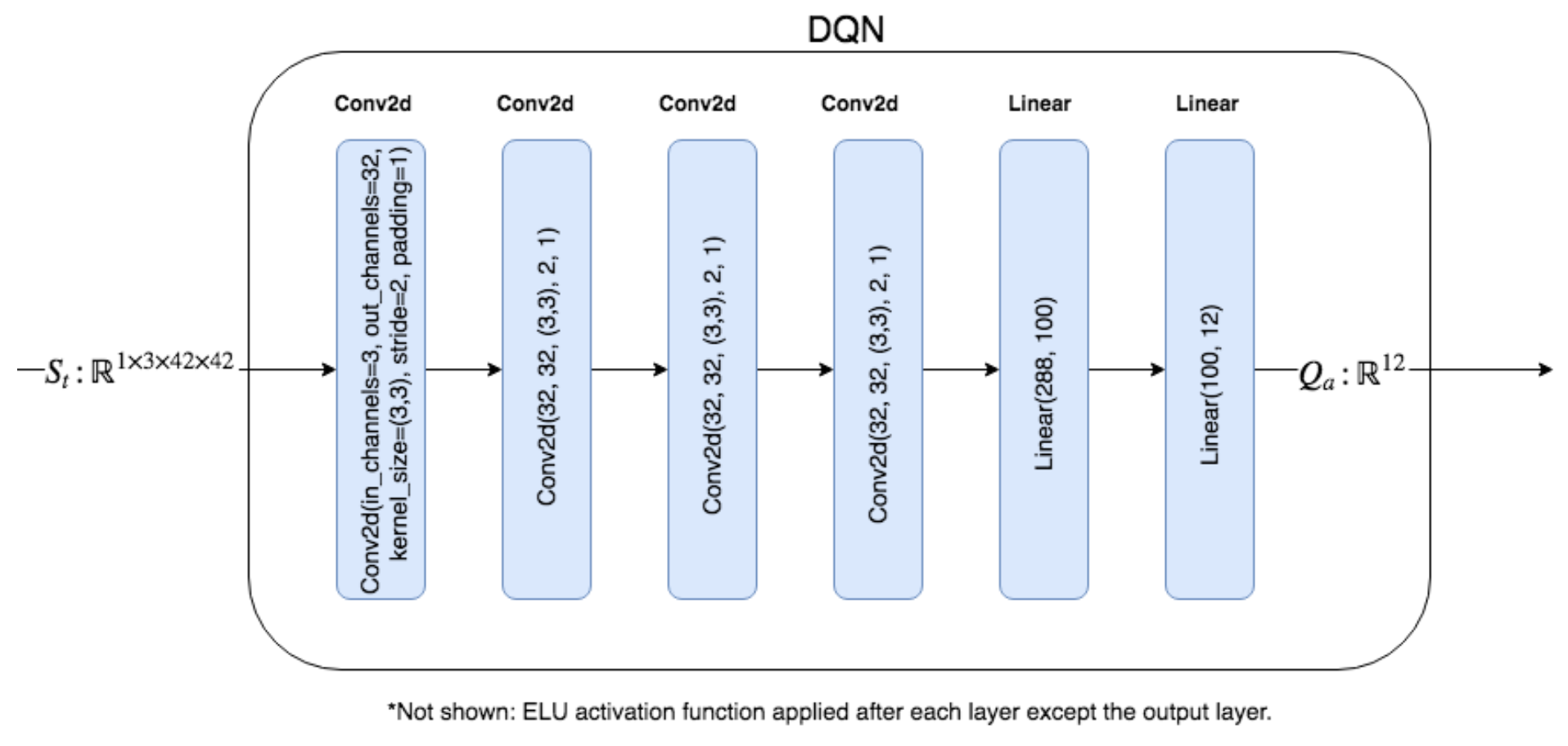
Figure 8.12: DQN 아키텍처 다이어그램이다. State 텐서는 입력이며 4개의 컨볼루션 레이어를 통과한 다음 2개의 선형 레이어를 통과한다. ELU 활성화 함수는 출력이 임의로 스케일된 Q-value을 생성할 수 있어야하기 때문에 처음 5개의 레이어 뒤에 적용되지만 출력 레이어에는 적용되지 않는다.

따라서 DQN은 State에 주어진 각 가능한 Action (예 : Action-value 또는 Q-value)에 대해 Expected Reward를 예측하는 법을 배우고, 이러한 Action-value를 이용하여 어떤 행동을 취할 것인지 결정한다. 안일하게 생각하면 우리는 Maximum Value인 Action를 취해야하지만, DQN은 학습 초기에는 정확한 Action-value를 생성하지 않으므로 DQN이 더 나은 Action-value 추정을 학습 할 수 있도록 약간의 탐험을 허용하는 Policy가 필요하다.

앞에서 확률이 ε인 Random Action을 취하고 확률이 1-ε인 가장 높은 값을 갖는 Action을 취하는 엡실론 탐욕 정책(Epsilon-Greedy Policy)의 사용에 대해 설명했다. 일반적으로 ε을 0.1과 같이 합리적으로 작은 확률로 설정하고 학습 중에 ε을 천천히 감소시켜 Maximum Value Action을 선택할 가능성이 점점 높아지게 만든다.

또한 Policy로서 softmax 함수에서의 샘플링에 대해 설명했다. softmax 함수는 기본적으로 임의의 실수로 벡터를 입력으로 들어가면 각 요소가 확률이고 모든 요소의 합이 1 인 동일한 크기의 벡터를 출력한다. 입력 벡터가 Action-value이면 Softmax 함수는 이산 확률 분포를 반환한다. Action-value가 가장 높은 액션에 가장 높은 확률이 할당되도록 만들고 반환되는 것은 Action-value를 기반으로 하는 Action에 대한 분포다. 이 분포에서 샘플링하면 가장 높은 값을 가진 Action이 더 자주 선택되지만 다른 Action도 선택된다. 이 접근법의 문제점은 Best Action(Action-value에 따른)이 다른 옵션보다 약간 우수할 경우, 상당히 높은 빈도로 더 나쁜 Action이 여전히 선택된다는 것이다. 예를 들어, 아래에서는 5개의 Action에 대해 Action-value 텐서를 가져 와서 PyTorch의 함수 모듈에서 softmax 함수를 적용한다.

>>> torch.nn.functional.softmax(th.Tensor([3.6, 4, 3, 2.9, 3.5]))
tensor([0.2251, 0.3358, 0.1235, 0.1118, 0.2037])

보시다시피 최상의 Action(인덱스 1)은 다른 Action보다 약간 우수하므로 모든 Action의 가능성이 매우 높으며이 Policy는 Uniform Random Policy와 크게 다르지 않다. 학습 초기단계에서는 탐험을 장려하기 위해 Softmax Policy로 시작할 것이며, 고정 된 수의 단계 이후에는 엡실론 탐욕 전략(Epsilon-Greedy Policy)으로 전환하여 탐험을 계속하지만 대부분 Best Action을 취할 것이다.

Listing 8.5 : Policy 함수

def policy(qvalues, eps=None): #A
    if eps is not None:
        if torch.rand(1) < eps:
            return torch.randint(low=0,high=7,size=(1,))
        else:
            return torch.argmax(qvalues)
    else:
        return torch.multinomial(F.softmax(F.normalize(qvalues)), num_samples=1) #B


#A Policy 함수는 Action-value 벡터와 엡실론(eps) 매개 변수를 사용한다.
#B eps가 제공되지 않으면 Softmax Policy를 사용한다. multinomial 함수를 사용하여 softmax에서 샘플링한다.

DQN에 필요한 또 다른 큰 구성 요소는 Experience Replay Memory이다. 그라디언트가 너무 노이지하기 때문에 한 번에 하나의 데이터 샘플만 전달하면 그라디언트 기반 최적화(Gradient-based Optimization)가 제대로 작동하지 않는다. 노이지한 그래디언트를 평균하기 위해 충분히 큰 샘플(배치 또는 미니 배치라고 함)을 가져와 모든 샘플의 그래디언트를 평균 또는 합산한다. 게임을 할 때는 한 번에 하나의 데이터 샘플만 볼 수 있기 때문에 대신 Experience을 “메모리(Memory)” 저장소에 저장한 다음 메모리에서 미니 배치를 샘플링하여 학습한다. 각 튜플의 형식 (St, at, rt, St + 1)인 튜플의 Experience를 저장하는 List가 포함된 Experience Replay 파이썬 클래스를 만든다. 이 클래스에는 메모리를 추가하고 미니 배치를 샘플링하는 메소드도 있다.

Listing 8.6 : Experience Replay

from random import shuffle
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F

class ExperienceReplay:
    def __init__(self, N=500, batch_size=100):
        self.N = N #A
        self.batch_size = batch_size #B
        self.memory = []
        self.counter = 0

    def add_memory(self, state1, action, reward, state2):
        self.counter +=1
        if self.counter % 500 == 0: #C
            self.shuffle_memory()

        if len(self.memory) < self.N: #D
            self.memory.append( (state1, action, reward, state2) )
        else:
            rand_index = np.random.randint(0,self.N-1)
            self.memory[rand_index] = (state1, action, reward, state2)

    def shuffle_memory(self): #E
        shuffle(self.memory)

    def get_batch(self): #F
        if len(self.memory) < self.batch_size:
            batch_size = len(self.memory)
        else:
            batch_size = self.batch_size
        if len(self.memory) < 1:
            print("Error: No data in memory.")
            return None
        #G
        ind = np.random.choice(np.arange(len(self.memory)),batch_size,replace=False)
        batch = [self.memory[i] for i in ind] #batch is a list of tuples
        state1_batch = torch.stack([x[0].squeeze(dim=0) for x in batch],dim=0)
        action_batch = torch.Tensor([x[1] for x in batch]).long()
        reward_batch = torch.Tensor([x[2] for x in batch])
        state2_batch = torch.stack([x[3].squeeze(dim=0) for x in batch],dim=0)
        return state1_batch, action_batch, reward_batch, state2_batch


#A N은 메모리 List의 최대 크기이다.
#B batch_size는 get_batch (...) 메소드를 사용하여 메모리에서 생성할 샘플 수이다.
#C 메모리에 튜플을 추가시 500회 반복 할 때마다 메모리 샘플을 섞어서 보다 랜덤한 샘플을 만든다.
#D 메모리가 가득 차지 않았으면 List에 추가한다. 메모리가 가득찼으면 임의의 메모리를 새 것으로 교체한다.
#E Python의 내장 셔플 함수를 사용하여 메모리 List를 셔플링한다.
#F 메모리 List에서 미니 배치를 무작위로 샘플링한다.
#G 인덱스를 나타내는 임의의 정수 배열을 만든다.

Experience Replay 클래스는 기본적으로 List을 Wrapping했기 때문에 List의 추가 함수들을 사용할 수 있다. List의 추가 함수는 튜플을 추가 할 때 최대 수(maximum number가 정해져 있음)까지만 가능하며, List에서 샘플링도 할 수 있어야 한다. get_batch(…) 메소드로 샘플링하면 메모리 List의 인덱스를 나타내는 임의의 정수 배열을 만든다. 이 인덱스를 사용하여 메모리 List에 인덱스를 생성하여 임의의 메모리 샘플을 검색한다. 각 샘플은 튜플 (St, at, rt, St + 1)이므로 서로 다른 구성 요소를 분리하여 St 텐서, at 텐서 등에 쌓으려고 한다. 여기서 배열의 첫 번째 차원이 배치 크기(Batch size)이다. 예를 들어, 반환하려는 St 텐서의 크기는 batch_size × 3 (채널) × 42 (높이) × 42 (폭) 이어야 한다. PyTorch의 stack (…) 함수는 개별 텐서 List를 단일 텐서로 연결한다. 또한 크기 1의 차원을 제거하고 추가하기 위해 squeeze (…) 및 unsqueeze (…) 메소드를 사용한다.

이러한 이 모든 설정을 통해 학습 루프 자체 외에도 vanilla DQN을 학습하는 데 필요한 것을 다루었다. 다음 섹션에서는 본질적 호기심 모듈 (ICM, Intrinsic Curiosity Module)을 구현할 것이다.

8.6 본질적 호기심 모듈(Intrinsic Curiosity Module)

앞에서 설명한 것처럼 ICM은 3개의 독립적인 신경망 모델 (순방향 모델, 인보스 모델 및 인코더)로 구성된다. 순방향 모델은 현재 (인코딩 된) State와 Action이 주어진 다음 (인코딩 된) State를 예측하도록 훈련된다. 인버스 모델은 두 개의 연속적인 (인코딩 된) State φ(St) 및 φ(St + 1)가 주어진 Action을 예측하도록 훈련된다. 인코더는 단순히 원시 3채널 State를 단일 저차원 벡터로 변환한다. 인버스 모델은 Action 예측과 관련된 정보만 보존하는 방식으로 인코더가 State를 인코딩하는 것을 학습하도록 간접적으로 작동한다.

Figure 8.13: 본질적 호기심 모듈 (ICM)에 대한 상위수준 개요. ICM에는 각각 별도의 신경망인 3개의 구성 요소가 있다. 인코더 모델은 State를 저차원 벡터로 인코딩하며, 두 개의 연속 State 사이에서 수행된 Action을 예측하려고 하는 인버스 모델을 통해 간접적으로 학습된다. 순방향 모델은 다음 인코딩된 State를 예측하고 그 오류는 본질적 보상(Intrinsic Reward)으로 사용되는 예측 오류이다.

순방향 모델은 선형 레이어가 있는 간단한 2계층 신경망이다. 순방향 모델에 대한 입력은 State φ(St)를 Action at와 연결하여 구성된다. 인코딩된 State φ(St)는 텐서 B x 288이고 Action at∶B × 1 은 액션 인덱스를 나타내는 정수의 배치이므로, 크기가 12인 벡터를 만들고 at 의 인덱스를 12로 설정하여 one-hot 인코딩된 벡터를 만든다. 그런 다음이 두 텐서를 연결하여 배치 x 288 + 12 = 배치 x 300 차원 텐서를 만든다. 첫 번째 레이어 뒤에 ReLU(Rectified Linear Unit) 활성화 유닛(Activation Unit)를 사용하지만 출력 레이어 뒤에는 활성화 함수를 사용하지 않는다. 출력 레이어는 B × 288 텐서를 생성한다.

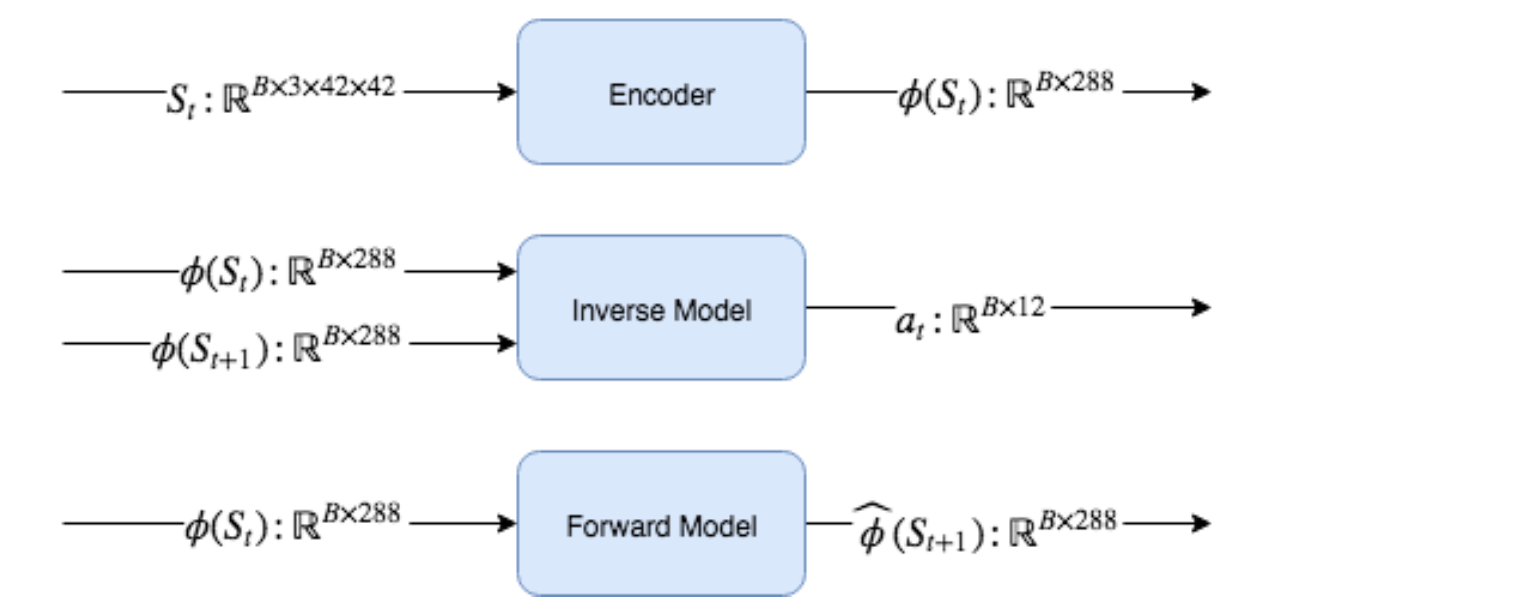
Figure 8.14 : ICM의 각 구성 요소에 대한 입력 및 출력의 유형과 차원을 보여준다.

인버스 모델은 선형 레이어가 있는 간단한 2 계층 신경망이다. 입력은 배치 x 288 + 288 = 배치 x 576 차원의 텐서를 만들기 위해 함께 연결된 두 개의 인코딩된 State St 및 St + 1이다. 첫번째 레이어 다음에 ReLU 활성화 함수를 사용한다. 출력 레이어는 Softmax 함수가 적용된 Batch x 12 차원의 텐서를 생성하여 동작에 대한 이산 확률 분포를 생성한다. 인버스 모델을 학습시킬 때, Action에 대한 이산 분포와 취해진 실제 행동의 one-hot 인코딩 벡터 사이의 오차를 계산한다.

인코더는 각 레이어 다음에 ELU 활성화 함수가 있는 4개의 컨볼루션 레이어(DQN과 동일한 아키텍처)로 구성된 신경망입니다. 그런 다음 최종 출력을 평탄화(Flatten)하여 288 차원의 평탄화된 벡터 출력을 얻는다.

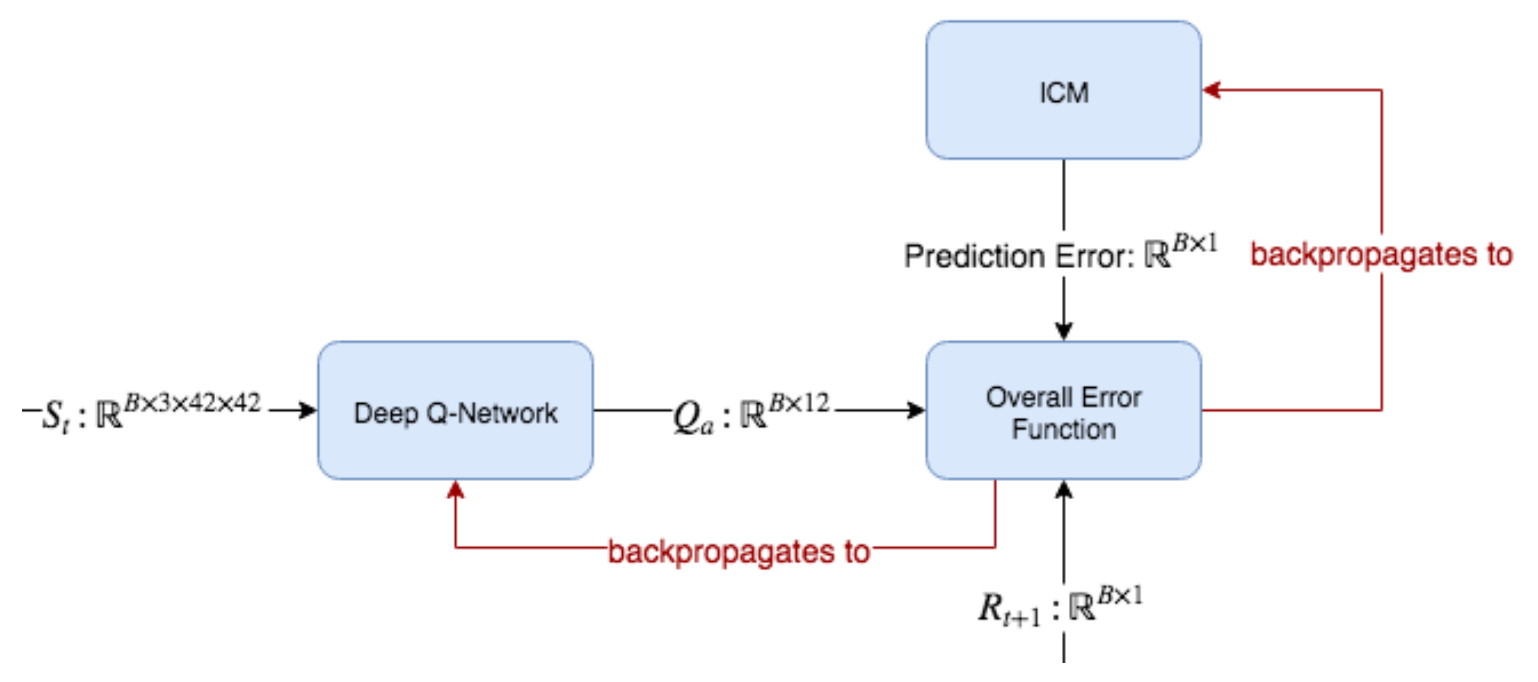
Figure 8.15: DQN 및 ICM은 DQN 및 ICM 매개 변수(parameter)를 최소화하기 위해 Optimizer에 제공되는 단일 전체 손실 함수(single overall loss function)에 기여한다. DQN의 Q-value 예측은 관측된 Reward와 비교된다. 그러나 관찰된 Reward는 새로운 Reward value를 얻기 위해 ICM의 예측 오류와 함께 합산된다.

ICM의 요점은 단일 수량(Single Quantity), 순방향 모델 예측 오류를 생성하는 것이다. 말 그대로 손실 함수에서 생성된 오류를 DQN의 본질적 보상(Intrinsic Reward)으로 사용한다. 최종 보상(Final Reward) rt = ri + re를 얻기 위해 이 본질적 보상(Intrinsic Reward)을 외적 보상(Extrinsic Reward)에 추가 할 수 있다. 최총 보상의 비율을 제어하기 위해 본질적 보상 또는 외적 보상을 조정할 수 있다.

다음은 에이전트 모델 (DQN)을 포함하여 보다 자세하게 표현한 ICM의 다이어그램이다.

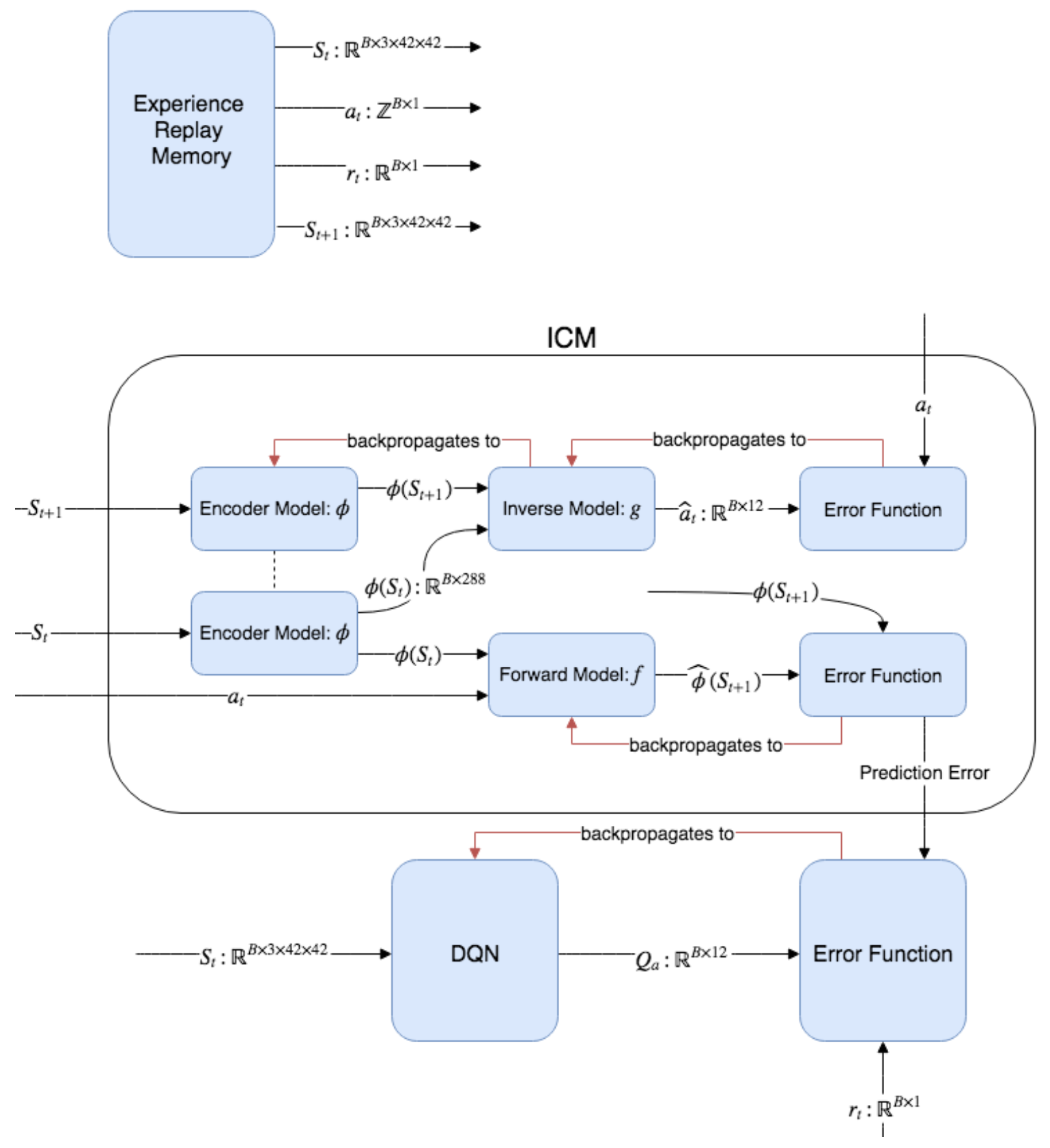
Figure 8.16: ICM을 포함한 전체 알고리즘 모습. 먼저 Experience Replay 메모리에서 샘플을 생성하여 ICM 및 DQN에서 사용한다. ICM을 순방향으로 실행하여 예측 오류를 생성한 다음 DQN의 오류 함수에 제공한다. 그런 다음 DQN은 외적(Extrinsic, 환경이 제공) Reward뿐만 아니라 본질적(Intrinsic, 예측 오류 기반) Reward를 반영하는 Action-value를 예측하는 법을 학습한다.

ICM의 구성 요소에 대한 코드를 보자.

Listing 8.7 : ICM 구성 요소

class Phi(nn.Module): #A
    def __init__(self):
        super(Phi, self).__init__()
        self.conv1 = nn.Conv2d(3, 32, kernel_size=(3,3), stride=2, padding=1)
        self.conv2 = nn.Conv2d(32, 32, kernel_size=(3,3), stride=2, padding=1)
        self.conv3 = nn.Conv2d(32, 32, kernel_size=(3,3), stride=2, padding=1)
        self.conv4 = nn.Conv2d(32, 32, kernel_size=(3,3), stride=2, padding=1)

    def forward(self,x):
        x = F.normalize(x)
        y = F.elu(self.conv1(x))
        y = F.elu(self.conv2(y))
        y = F.elu(self.conv3(y))
        y = F.elu(self.conv4(y)) #size [1, 32, 3, 3] batch, channels, 3 x 3
        y = y.flatten(start_dim=1) #size N, 288
        return y

class Gnet(nn.Module): #B
    def __init__(self):
        super(Gnet, self).__init__()
        self.linear1 = nn.Linear(576,256)
        self.linear2 = nn.Linear(256,12)

    def forward(self, state1,state2):
        x = torch.cat( (state1, state2) ,dim=1)
        y = F.relu(self.linear1(x))
        y = self.linear2(y)
        y = F.softmax(y,dim=1)
        return y

class Fnet(nn.Module): #C
    def __init__(self):
        super(Fnet, self).__init__()
        self.linear1 = nn.Linear(300,256)
        self.linear2 = nn.Linear(256,288)

    def forward(self,state,action):
        action_ = torch.zeros(action.shape[0],12) #D
        indices = torch.stack( (torch.arange(action.shape[0]), action.squeeze()), dim=0)
        indices = indices.tolist()
        action_[indices] = 1.
        x = torch.cat( (state,action_) ,dim=1)
        y = F.relu(self.linear1(x))
        y = self.linear2(y)
        return y

class Qnetwork(nn.Module):
    def __init__(self):
        super(Qnetwork, self).__init__()
        #in_channels, out_channels, kernel_size, stride=1, padding=0
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=32, kernel_size=(3,3), stride=2, padding=1)
        self.conv2 = nn.Conv2d(32, 32, kernel_size=(3,3), stride=2, padding=1)
        self.conv3 = nn.Conv2d(32, 32, kernel_size=(3,3), stride=2, padding=1)
        self.conv4 = nn.Conv2d(32, 32, kernel_size=(3,3), stride=2, padding=1)
        self.linear1 = nn.Linear(288,100)
        self.linear2 = nn.Linear(100,12)

    def forward(self,x):
        x = F.normalize(x)
        y = F.elu(self.conv1(x))
        y = F.elu(self.conv2(y))
        y = F.elu(self.conv3(y))
        y = F.elu(self.conv4(y))
        y = y.flatten(start_dim=2)
        y = y.view(y.shape[0], -1, 32)
        y = y.flatten(start_dim=1)
        y = F.elu(self.linear1(y))
        y = self.linear2(y) #size N, 12
        return y


#A Phi는 인코더 네트워크이다.
#B Gnet은 인버스 모델이다.
#C Fnet은 순방향 모델이다.
#D Action은 Replay Memory에 정수(Integer)로 저장되고 one-hot 인코딩된 벡터로 변환된다.

이러한 구성 요소 중 어느 것도 복잡한 아키텍처를 가지고 있지 않으며 상당히 평범하지만 구성 요소들이 모여 강력한 시스템을 만든다. ICM 구성 요소에 대해 살펴 봤으니 이제 하나로 만들어 보자. (St, at, St + 1)를 입력으로 받는 함수를 정의하겠다. 순방향 모델 예측 오류 및 인버스 모델 오류를 반환한다. 순방향 모델 오류는 순방향 모델을 역전파 및 학습시킬뿐만 아니라 DQN에 대한 본질적 보상으로도 사용된다. 인버스 모델 오차는 인버스 모델 및 인코더 모델을 역전파하고 학습시키는 데만 사용된다. 먼저 하이퍼파라미터 설정 및 모델의 인스턴스화를 살펴보자.

Listing 8.8 : 하이퍼파라미터 및 모델 인스턴스화

params = {
    'batch_size':150,
    'beta':0.2,
    'lambda':0.1,
    'eta': 1.0,
    'gamma':0.2,
    'max_episode_len':100,
    'min_progress':15,
    'action_repeats':6,
    'frames_per_state':3
}

replay = ExperienceReplay(N=1000, batch_size=params['batch_size'])
Qmodel = Qnetwork()
encoder = Phi()
forward_model = Fnet()
inverse_model = Gnet()
forward_loss = nn.MSELoss(reduction='none')
inverse_loss = nn.CrossEntropyLoss(reduction='none')
qloss = nn.MSELoss()
all_model_params = list(Qmodel.parameters()) + list(encoder.parameters()) #A
all_model_params += list(forward_model.parameters()) + list(inverse_model.parameters())
opt = optim.Adam(lr=0.001, params=all_model_params)


#A 각 모델의 파라미터를 단일 List에 추가하고 단일 Optimizer에 전달한다.

params 파이썬 Dictionary의 일부 매개 변수(Parameter)는 batch_size와 같이 친숙한 것도 있지만 다른 매개 변수는 그렇지 않을 것이다. 매개 변수를 살펴 보기 전에 전체 손실 함수를 먼저 살펴 보자.

다음은 4가지 모델 (DQN 포함)의 전체 손실에 대한 공식이다.

이 공식은 계수에 의해 각각 스케일링된 순방향 및 인버스 모델 손실과 함께 DQN 손실이 추가되어 있다. DQN 손실에는 자유 스케일링 매개 변수(free scaling parameter) λ가 있으며, 정방향 및 인버스 모델 손실은 스케일링 매개 변수 β를 공유하므로 서로 관련이 있다. 전체 손실 공식은 우리가 역전파하는 유일한 손실 함수이므로 각 학습 단계에서 이 단일 손실 함수에서 시작하여 4가지 모델 모두를 통해 전파한다.

max_episode_len 및 min_progress 매개 변수는 마리오가 수행해야하는 최소 진행률을 설정하는 데 사용된다. 때로는 마리오가 장애물 뒤에 갇혀 영원히 같은 Action을 계속할 수도 있다. 마리오가 적당한 시간 내에 충분히 전진하지 않으면 우리는 그가 갇혀있다고 가정하고 환경을 재기동해야 한다.

학습 중에 Policy 함수가 Action 3을 수행하도록 지시하면 실제로 Action을 한 번만 수행하는 대신 Action을 6 번 반복해 수행한다(action_repeats 매개 변수에 따라 설정 됨). 이것은 DQN이 Action의 value를 더 빨리 배우는 데 도움이 된다. 테스트(추론,Inference) 중에는 한 번만 Action을 취한다. 감마 매개 변수는 DQN 에서 사용된 것과 동일한 감마 매개 변수이다. DQN을 학습 할 때 Target 값은 현재 Reward rt뿐만 아니라 다음 State에 대해 가장 높은 예상 Action-value이므로 전체 Target은 rt + γ⋅max⁡ (Q(St + 1))이다. 마지막으로 frames_per_state는 각 State가 게임 플레이의 마지막 3프레임으로 만들어지도록 3으로 설정된다.

Listing 8.9 : 손실 함수

def loss_fn(q_loss, inverse_loss, forward_loss):
    loss_ = (1 - params['beta']) * inverse_loss
    loss_ += params['beta'] * forward_loss
    loss_ = loss_.sum() / loss_.flatten().shape[0]
    loss = loss_ + params['lambda'] * q_loss
    return loss

ICM 함수를 보자.

Listing 8.10 : ICM 예측 오류 계산

def ICM(state1, action, state2, forward_scale=1., inverse_scale=1e4):
    state1_hat = encoder(state1) #A
    state2_hat = encoder(state2)
    state2_hat_pred = forward_model(state1_hat.detach(), action.detach()) #B
    forward_pred_err = forward_scale * forward_loss(state2_hat_pred, \
                        state2_hat.detach()).sum(dim=1).unsqueeze(dim=1)
    pred_action = inverse_model(state1_hat, state2_hat) #C
    inverse_pred_err = inverse_scale * inverse_loss(pred_action, \
                                        action.detach().flatten()).unsqueeze(dim=1)
    return forward_pred_err, inverse_pred_err


#A 먼저 인코더 모델을 사용하여 state1과 state2를 인코딩한다.
#B 인코딩된 State를 사용하여 순방향 모델을 실행한다. 이 때 그래프에서 detach하는 것을 잊으면 안된다.
#C 인버스 모델은 Action에 대한 Softmax 확률 분포를 반환한다.

ICM을 실행할 때 그래프에서 노드를 올바르게 detach하는 것이 얼마나 중요한지를 반복해서 이야기하겠다. PyTorch (및 거의 모든 다른 기계 학습 라이브러리)는 노드가 개별 텐서이고 노드 간 연결이 그 사이의 Operation인 계산 그래프(Computational Graph)를 만든다. .detach() 메소드를 호출하여 계산 그래프에서 텐서를 분리하고 원시 데이터(raw data)처럼 처리한다. 이는 PyTorch가 해당 노드를 통해 역전파되는 것을 방지한다. 순방향 모델과 그 손실 함수를 실행할 때 state1_hat 및 state2_hat 텐서를 분리하지 않으면 순방향 모델이 인코더로 역전파되어 인코더 모델이 손상된다.

이제 주요 학습 과정을 살펴보자. Experience Replay를 사용하고 있으므로 학습은 Replay Buffer에서 샘플링 할 때만 발생한다. Replay Buffer에서 샘플링하여 개별 모델 오류를 계산하는 함수를 설정할 것이다.

Listing 8.11 : Experience Replay를 사용한 미니 배치 학습

def minibatch_train(use_extrinsic=True):
    state1_batch, action_batch, reward_batch, state2_batch = replay.get_batch()
    action_batch = action_batch.view(action_batch.shape[0],1) #A
    reward_batch = reward_batch.view(reward_batch.shape[0],1)

    forward_pred_err, inverse_pred_err = ICM(state1_batch, action_batch, state2_batch) #B
    i_reward = (1. / params['eta']) * forward_pred_err #C
    reward = i_reward.detach() #D
    if use_explicit: #E
        reward += reward_batch
    qvals = Qmodel(state2_batch) #F
    reward += params['gamma'] * torch.max(qvals)
    reward_pred = Qmodel(state1_batch)
    reward_target = reward_pred.clone()
    indices = torch.stack( (torch.arange(action_batch.shape[0]), \ #G
    action_batch.squeeze()), dim=0)
    indices = indices.tolist()
    reward_target[indices] = reward.squeeze()
    q_loss = 1e5 * qloss(F.normalize(reward_pred), F.normalize(reward_target.detach()))
    return forward_pred_err, inverse_pred_err, q_loss


#A 모델과 호환되도록 단일 차원을 추가하기 위해 텐서의 형태를 변경한다.
#B ICM 실행
#C eta 매개 변수를 사용하여 순방향 예측 오류를 스케일한다.
#D Reward의 합을 구한다. i_reward 텐서를 detach하는 것을 잊지 말아야 한다.
#E use_explicit 부울 변수를 사용하면 본질적 보상(Intrinsic Reward) 외에 명시적 보상(Explicit Reward)을 사용할지 여부를 결정할 수 있다.
#F 다음 State에 대한 Action-value를 계산하고 이것을 Target Reward 식에 추가하기 위해 사용한다.
#G action_batch는 정수의 Action 인덱스 텐서이므로 이를 one-hot 인코딩 벡터의 텐서로 변환한다.

주요 학습 과정을 알아 보겠다. 앞에서 정의한 prepare_initial_state(…) 함수를 사용하여 첫번째 State를 초기화한다. 이 함수는 첫번째 프레임만 가져 와서 채널 차원을 따라 3번 반복한다. 또한 각 프레임을 관찰 할 때 추가 할 deque 인스턴스도 설정했다. deque는 maxlen이 3으로 설정되므로 가장 최근 3개의 프레임만 저장된다. Q-network로 전달하기 전에 먼저 deque를 List로 변환한 다음 1x3x42x42 차원의 PyTorch 텐서로 변환한다.

Listing 8.12 : 학습 루프

epochs = 5000
env.reset()
state1 = prepare_initial_state(env.render('rgb_array'))
eps=0.15
losses = []
episode_length = 0
switch_to_eps_greedy = 1000
state_deque = deque(maxlen=params['frames_per_state'])
e_reward = 0.
last_x_pos = env.env.env._x_position #A
ep_lengths = []
use_explicit = False
for i in range(epochs):
    opt.zero_grad()
    episode_length += 1
    q_val_pred = Qmodel(state1) #B
    if i > switch_to_eps_greedy: #C
        action = int(policy(q_val_pred,eps))
    else:
        action = int(policy(q_val_pred))
    for j in range(params['action_repeats']): #D
        state2, e_reward_, done, info = env.step(action)
        last_x_pos = info['x_pos']
        if done:
            state1 = reset_env()
            break
        e_reward += e_reward_
        state_deque.append(prepare_state(state2))
    state2 = torch.stack(list(state_deque),dim=1) #E
    replay.add_memory(state1, action, e_reward, state2) #F
    e_reward = 0
    if episode_length > params['max_episode_len']: #G
        if (info['x_pos'] - last_x_pos) < params['min_progress']:
            done = True
        else:
            last_x_pos = info['x_pos']
    if done:
        ep_lengths.append(info['x_pos'])
        state1 = reset_env()
        last_x_pos = env.env.env._x_position
        episode_length = 0
    else:
        state1 = state2
    if len(replay.memory) < params['batch_size']:
        continue
    forward_pred_err, inverse_pred_err, q_loss = minibatch_train(use_extrinsic=False) #H
    loss = loss_fn(q_loss, forward_pred_err, inverse_pred_err) #I
    loss_list = (q_loss.mean(), forward_pred_err.flatten().mean(),\
    inverse_pred_err.flatten().mean())
    losses.append(loss_list)
    loss.backward()
    opt.step()


#A 순방향 프로세스에 처리할 데이터가 없는 경우에는 Reset해야 하는데, 이를 위해서는  마지막 x 위치가 어디인지 추적해야 한다.
#B Action-value 예측을 얻기 위해 DQN을 순방향 실행한다.
#C 첫 1000 Epoch 후 Epsilon-Greedy Policy로 전환한다.
#D 학습 속도를 높이기 위해 Policy에 따른 Action을 6번 반복한다.
#E deque 객체를 텐서로 변환한다.
#F Replay Buffer에 단일 Experience를 추가한다.
#G 마리오가 앞으로 진행하지 않은 경우 게임을 Reset하고 다시 시도한다.
#H Replay Buffer로 부터 오는 한 개의 미니 배치로 부터 오류를 가져온다.

조금 길지만, 이 학습 루프는 매우 간단하다. State를 준비하고, DQN에 입력하고, Action-value(Q-value)를 얻고, Policy에 입력하고, 수행할 Action을 얻은 다음 env.step(action) 메소드를 호출하여 Action을 수행하기 만하면 된다. 그런 다음 다음 State와 다른 메타 데이터를 얻는다. 이 전체 Experience를 튜플 (St, at, rt, St + 1) 형태로 Experience Replay에 추가한다. 대부분의 Action은 이미 다룬 미니 배치 학습 함수에서 이루어지고 있으니 참고한다.

Super Mario Bros.를 학습하기 위해 End-to-End DQN 및 ICM을 구축하는 데 필요한 모든 주요 코드는 MacBook Air에서 실행되어 약 30 분 정도 걸리는 5000 epoch 학습 과정을 통해 테스트 해 볼 수 있다. (GPU 없이 테스트 가능함). 우리는 minibatch 함수에서 use_extrinsic = False를 사용하여 학습 할 것이므로 본질적 보상(Intrinsic Reward)에 대해서만 학습하고 있다. 다음 코드를 사용하여 각 ICM 구성 요소 및 DQN에 대한 개별 손실을 시각화 할 수 있다. 손실 데이터를 로그 스케일로 변환하여 비슷한 규모로 유지한다.

>>> losses_ = np.array(losses)
>>> plt.figure(figsize=(8,6))
>>> plt.plot(np.log(losses_[:,0]),label='Q loss')
>>> plt.plot(np.log(losses_[:,1]),label='Forward loss')
>>> plt.plot(np.log(losses [:,2]),label='Inverse loss')
>>> plt.legend()
>>> plt.show()

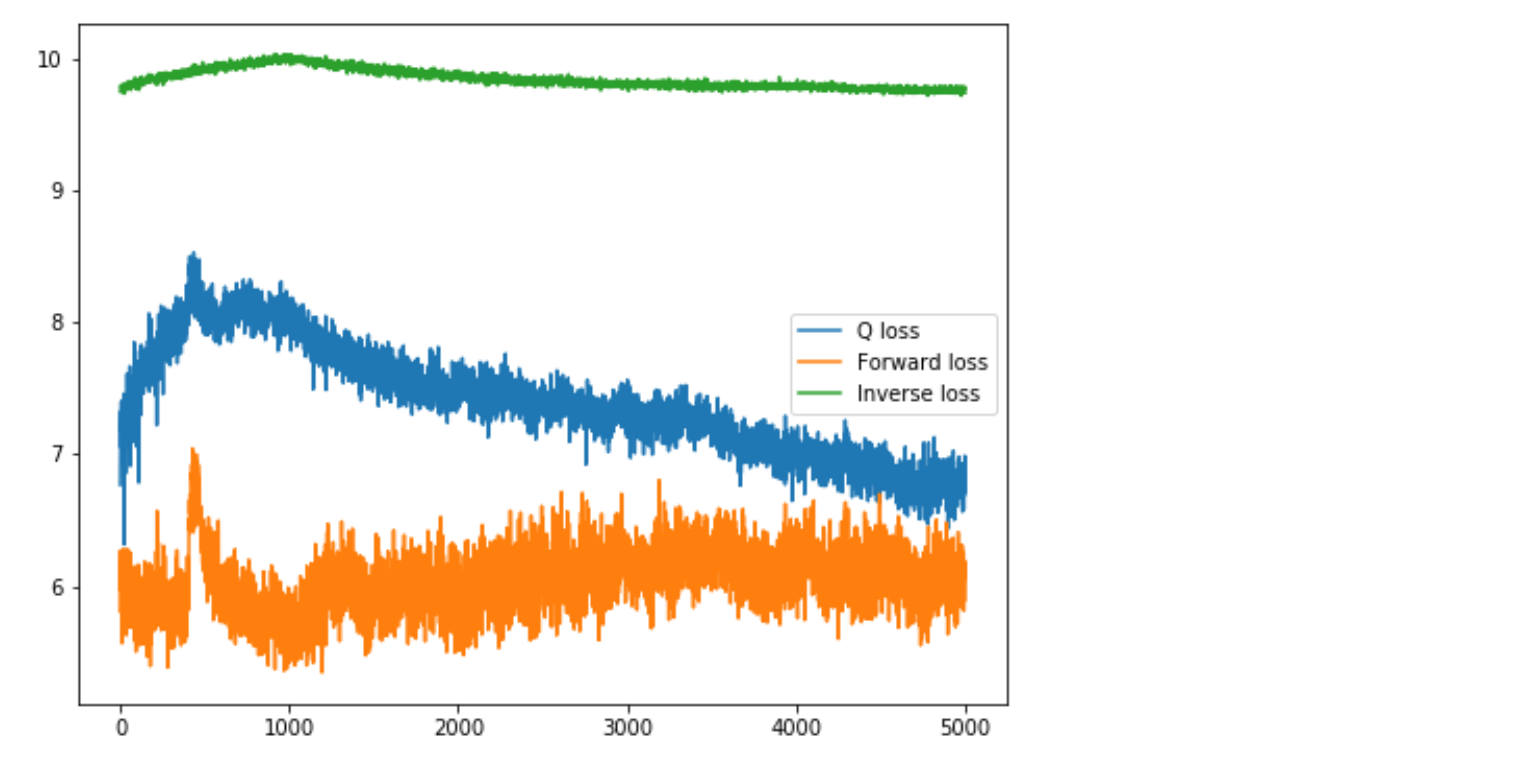
Figure 8.17: ICM 및 DQN의 개별 구성 요소에 대한 손실이다. DQN과 ICM이 적대적으로 학습되기 때문에 기존 단일 지도 신경망(supervised neural network)의 학습과정에서 익숙하게 보았던 것처럼 손실이 부드럽게 감소하지 않는다.

DQN 손실은 처음에 증가한 이후 분명하게 하락 추세이다. 순방향 손실은 급격한 상승 또는 하락 추세없이 노이지해 보인다. 인버스 모델은 다소 평탄한 것처럼 보이지만 확대하면 시간이 지남에 따라 매우 느리게 감소하는 것처럼 보인다. use_extrinsic = True를 설정하고 외적 보상을 사용하면 손실 그래프가 훨씬 좋아 보인다. 그러나 손실 그래프에 실망하지 않아도 된다. 학습된 DQN을 테스트하면 손실 그래프가 보여주는 것보다 훨씬 더 잘 수행된다. 순방향 모델이 예측 오류를 낮추려고 하지만 DQN은 예측 오류를 최대화하려고 하기 때문에 에이전트를 예측할 수 없는 환경의 State로 몰아감으로써 ICM과 DQN이 적대적 동적 시스템(Adversarial Dynamical System)처럼 작동하기 때문이다.

GAN(Generative Adversarial Network)에 대한 손실 그래프를 보면 생성기(Generator) 와 판별기(Discriminator) 손실은 DQN 및 use_extrinsic = False를 사용한 순방향 모델 손실과 다소 유사해 보인다. 단일 머신 러닝 모델을 학습 과정에서 익숙하게 보았던 것처럼 손실이 부드럽게 감소하지 않는다.

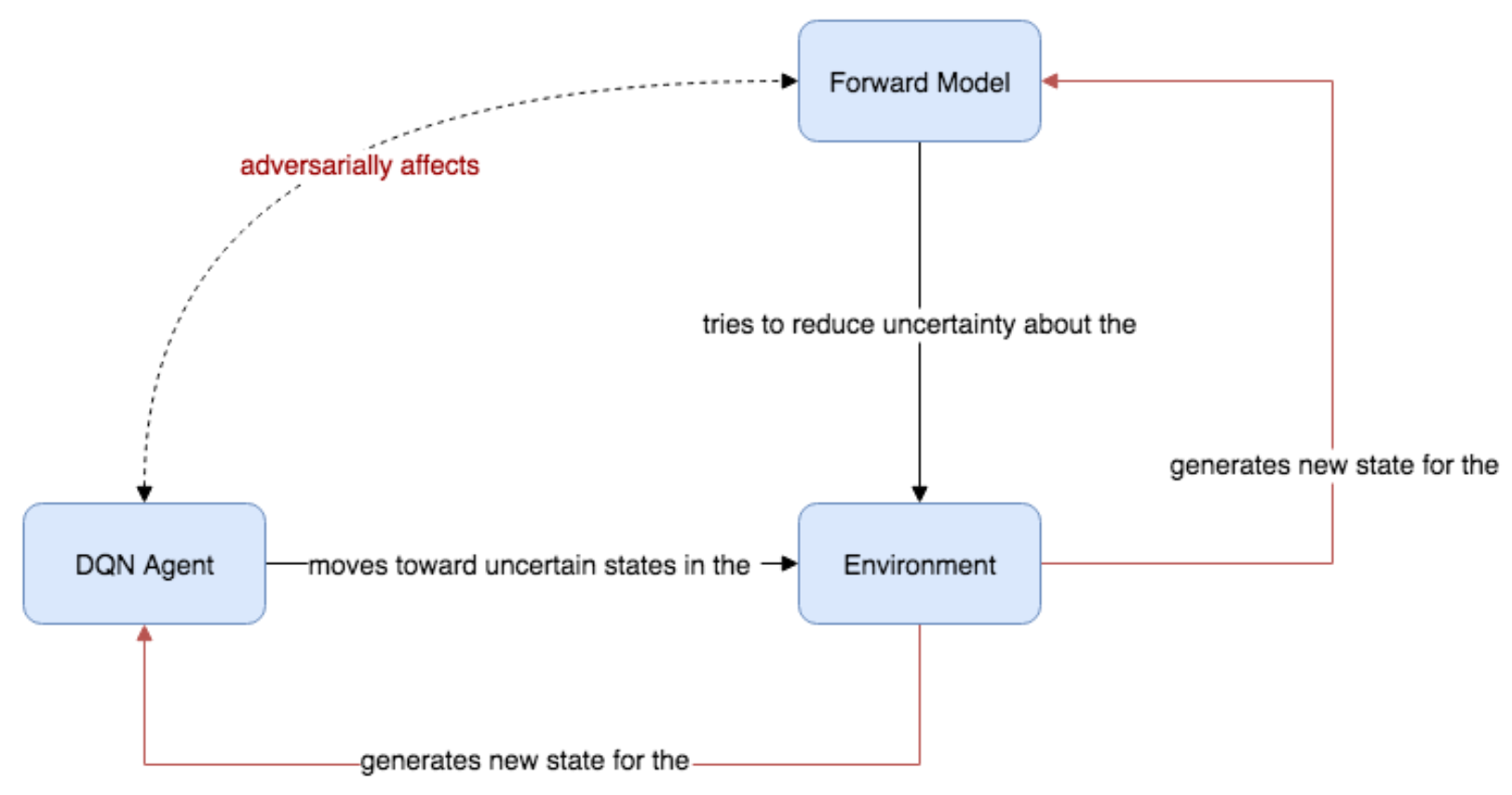
Figure 8.18: DQN 에이전트와 순반향 모델은 적대적 목적(antagonistic objectives)를 최적화하여 적대적 쌍(Adversarial Pair)을 구성한다.

전체 학습이 얼마나 잘 진행되고 있는지에 대한 더 나은 평가방법은 시간이 지남에 따라 에피소드 길이를 추적하는 것이다. 에이전트가 환경을 보다 효과적으로 진행하는 방법을 학습한 경우라면 에피소드 길이가 증가해야 한다. 학습 과정에서 에피소드가 끝날 때마다 (즉, 에이전트가 사망하거나 에이전트가 충분한 단계로 진행하지 않았는데 done 변수가 True가 되버리는 경우) 현재 info[ ‘x_pos’]를 ep_lengths List에 저장한다. 학습 시간이 지남에 따라 최대 에피소드 길이가 점점 길어질 것이다.

>>> plt.figure()
>>> plt.plot(losses_[:,3], label=’Episode length’)

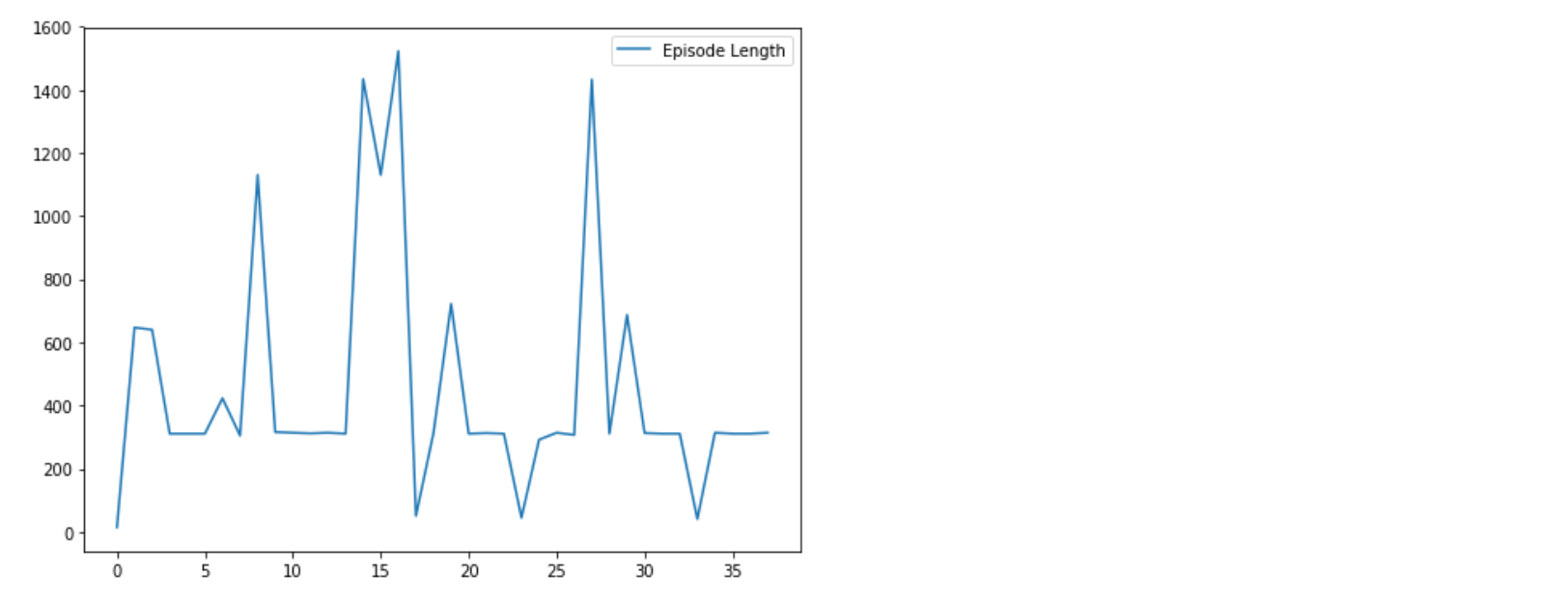
Figure 8.19: 학습 시간은 x축이며 에피소드 길이는 Y축이다. 학습 시간이 지남에 따라 점점 더 크게 급증하는 것을 볼 수 있다.

가장 큰 스파이크가 초기에 650점(게임에서 x 포지션)에 도달하고 있지만 15번째 에피소드까지 학습 시간이 지났을 때를 보면 에이전트는 x 포지션인 1500 보다 더 멀리 갈 수 있다.

에피소드 길이에 대한 시각화는 좋아 보인다. 실제로 Super Mario Bros를 플레이하는 학습된 에이전트의 비디오를 렌더링해 보겠다. 자신의 컴퓨터에서 이 게임을 실행하는 경우 OpenAI Gym은 라이브 게임 플레이로 새 창을 여는 렌더링 기능을 제공합니다.. 불행히도 원격 컴퓨터 또는 클라우드 가상 컴퓨터를 사용하는 경우 작동하지 않는다. 이 경우 가장 쉬운 대안은 루프에서 plt.imshow(env.render(“rgb_array”))를 사용하는 것이다.

Listing 8.13 : 학습된 에이전트 테스트

done = True
state_deque = deque(maxlen=params['frames_per_state'])
for step in range(5000):
    if done:
        env.reset()
        state1 = prepare_initial_state(env.render('rgb_array'))
    q_val_pred = Qmodel(state1)
    action = int(policy(q_val_pred,eps))
    state2, reward, done, info = env.step(action)
    state2 = prepare_multi_state(state1,state2)
    state1=state2
    env.render()

학습 루프로 부터 네트워크를 실행하고 Action을 취하는 코드 부분을 뽑아 왔기때문에 학습 루프를 따랐다면 여기에 설명할 것이 많지 않다. 여전히 Epsilon이 0.1로 설정된 Epsilon-Greedy Policy을 사용한다. 추론(Inference) 중에도 에이전트는 에이전트가 고착되는 것을 막기 위해 약간의 임의성(Randomness)이 필요하다. 주목해야 할 한 가지 차이점은 테스트(또는 추론) 모드에서 학습 모드에서 한 것처럼 6회가 아니라 한 번만 Action을 시행한다는 것이다. 여러분이 동일한 결과를 얻었다고 가정하면, 학습한 에이전트가 상당히 일관된 발전을 이루어 장애물들을 뛰어 넘을 수 있어야 한다. 축하한다!

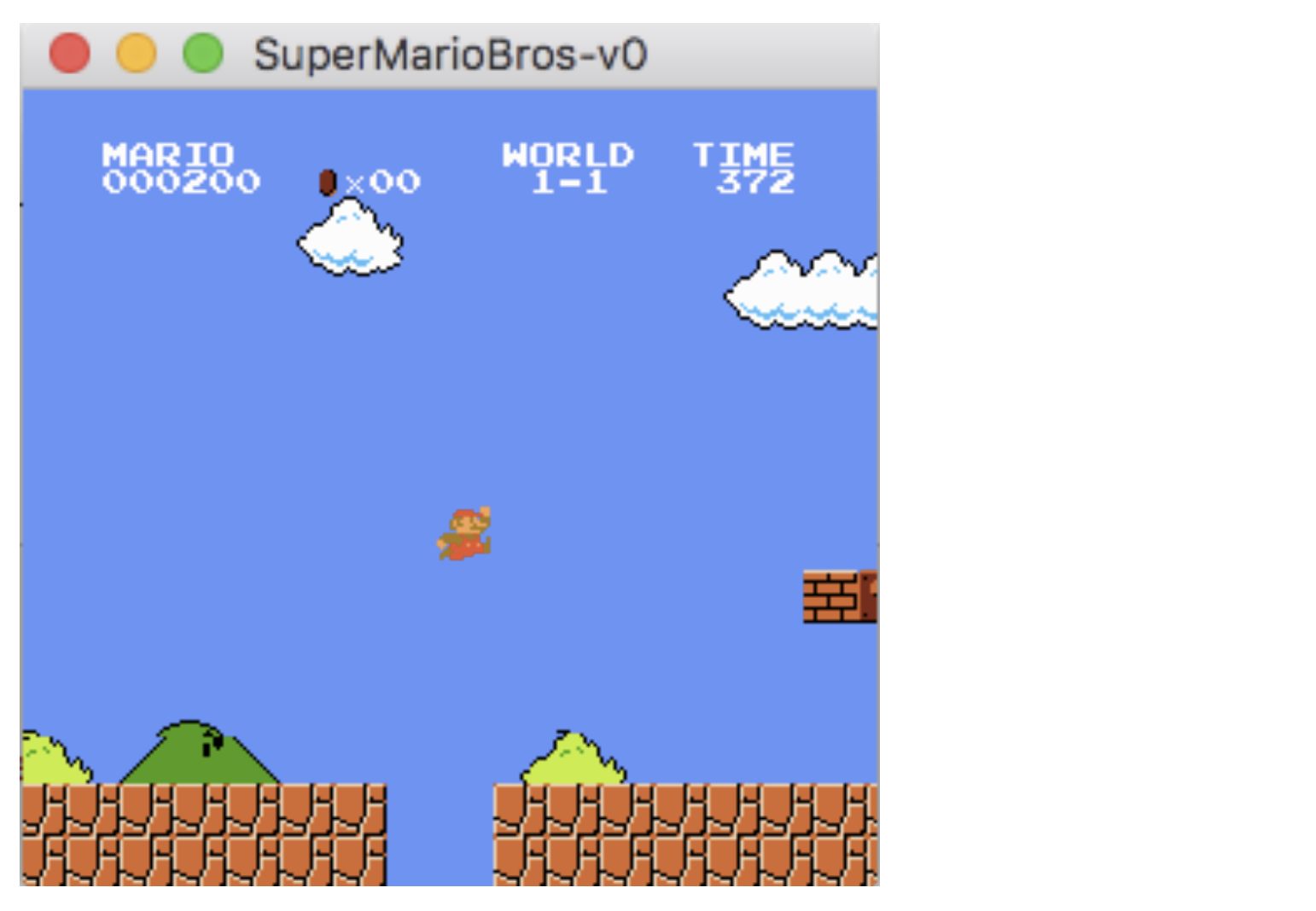
Figure 8.20: 마리오 에이전트가 본질적 보상(Intrinsic Reward)으로만 학습하여 구덩이를 성공적으로 뛰어 넘었다. 이를 통해 명백한 보상(Explicit Reward)없이 기본 기술을 익혔음을 알 수 있다. Random Policy로 에이전트는 앞으로 나아갈 수 없었다.

같은 결과를 얻지 못하면 하이퍼파라미터, 특히 학습 속도(learning rate), 미니 배치 크기(minibatch size), 최대 에피소드 길이(maximum episode length) 및 최소 진행률(minimum forward process)을 변경해 보자. 본질적 보상(Intrinsic Reward)이 있는 5000 Epoch 학습은 효과가 있지만 다양한 실험으로부터 경험한 바로는 하이퍼파라미터에 민감하다.

다른 환경에서는 어떻게 작동하는가?

우리가 “Super Mario Bros.” 라는 단일 게임 환경에서 ICM 기반 Reward로 DQN 에이전트를 학습하여 연구하는 동안 Burda et al. 팀은 “Large-Scale Study of Curiosity-Driven Learning” 논문을 통해서 2018년 본질적 보상(Intrinsic Reward)이 얼마나 효과적인지 입증했다. 그들은 여러 게임에서 Curiosity-based Reward를 사용하여 수많은 실험을 수행하여 호기심 많은 에이전트가 Super Mario Bros.에서 11 레벨을 진행하고 탁구(Pong) 등을 학습 있음을 발견했다. 기본적으로 방금 구축한 것과 동일한 ICM을 사용했지만 DQN 대신 PPO(Proximal Policy Optimization)라는 보다 정교한 에이전트 모델을 사용했다. 시도 할 수 있는 실험은 인코더 네트워크를 Random Projection으로 교체하는 것이다. Random Projection은 입력 데이터에 랜덤 초기화 매트릭스(randomly initializing matrix, 예 : 고정되고 학습되지 않은 랜덤하게 초기화된 신경망)를 곱하는 것을 말한다. Burda at al. 2018 논문은 학습된 인코더뿐만 아니라 Random Projection도 효과가 있음을 보여주었다.

8.7 본질적 보상(Intrinsic Reward) 메커니즘의 다른 대안들

이 장에서는 Reward이 적은 환경에서 RL 에이전트가 직면한 심각한 문제에 대해 설명했다. 이 문제를 호기심을 가진 에이전트를 이용해서 풀수 있다고 생각했다. 이 장에서는 최근 몇 년 동안 강화 학습 연구에서 가장 널리 인용 된 논문 중 하나인 Pathak et al. 2017 논문의 접근 방식을 구현했다. 이 접근 방식이 대중적인 것 뿐만아니라 너무 많은 새로운 개념을 도입하지 않고도 이전 장에서 배운 내용을 구축할수 있기 때문에 이 방법을 구현해 보기로 선택했다. 호기심 기반 학습(Curiosity-based learning, 이 외에도 여러 다른 이름으로 불림)은 매우 활발한 연구 분야이며, 많은 대안이 있으며, 그 중 일부는 ICM보다 낫다.

다른 흥미로운 방법들 중 다수는 베이지안 추론과 정보 이론을 이용하여 호기심을 유발할 수 있는 새로운 메커니즘을 제시한다. 이 장에서 우리가 사용한 예측 오류 (Prediction Error, PE) 접근 방식은 더 넓은 PE 우산 아래에 있는 구현물 중 하나이다. 우리가 지금 알고 있듯이, 기본적인 아이디어는 에이전트가 PE를 줄이려고 하거나 (즉, 환경에 대한 불확실성을 줄이려고 하거나) 예상치 못한 일에 놀라지 않도록 경험하지 않은 새로운 것들을 적극적으로 찾아나가야 한다는 것이다.

또 다른 우산은 에이전트 권한 부여(Agent Empowerment)이다. 권한 부여 전략(Empowerment Strategies)은 예측 오류를 최소화하고 환경을 보다 예측 가능하게 만들려고 하지 않고 에이전트를 최적화하여 환경에 대한 제어를 최대화한다. 이 분야의 한 논문은 Mohamed et al. 의 2015 논문인 “Variational Information Maximisation for Intrinsically Motivated Reinforcement Learning” 이다. 환경에 대한 통제를 극대화하는 것에 관한이 비공식적인 진술(statement)을 정확한 수학적 진술(mathematical statement, 수학적으로 근사하는 공식)로 만들 수 있다.

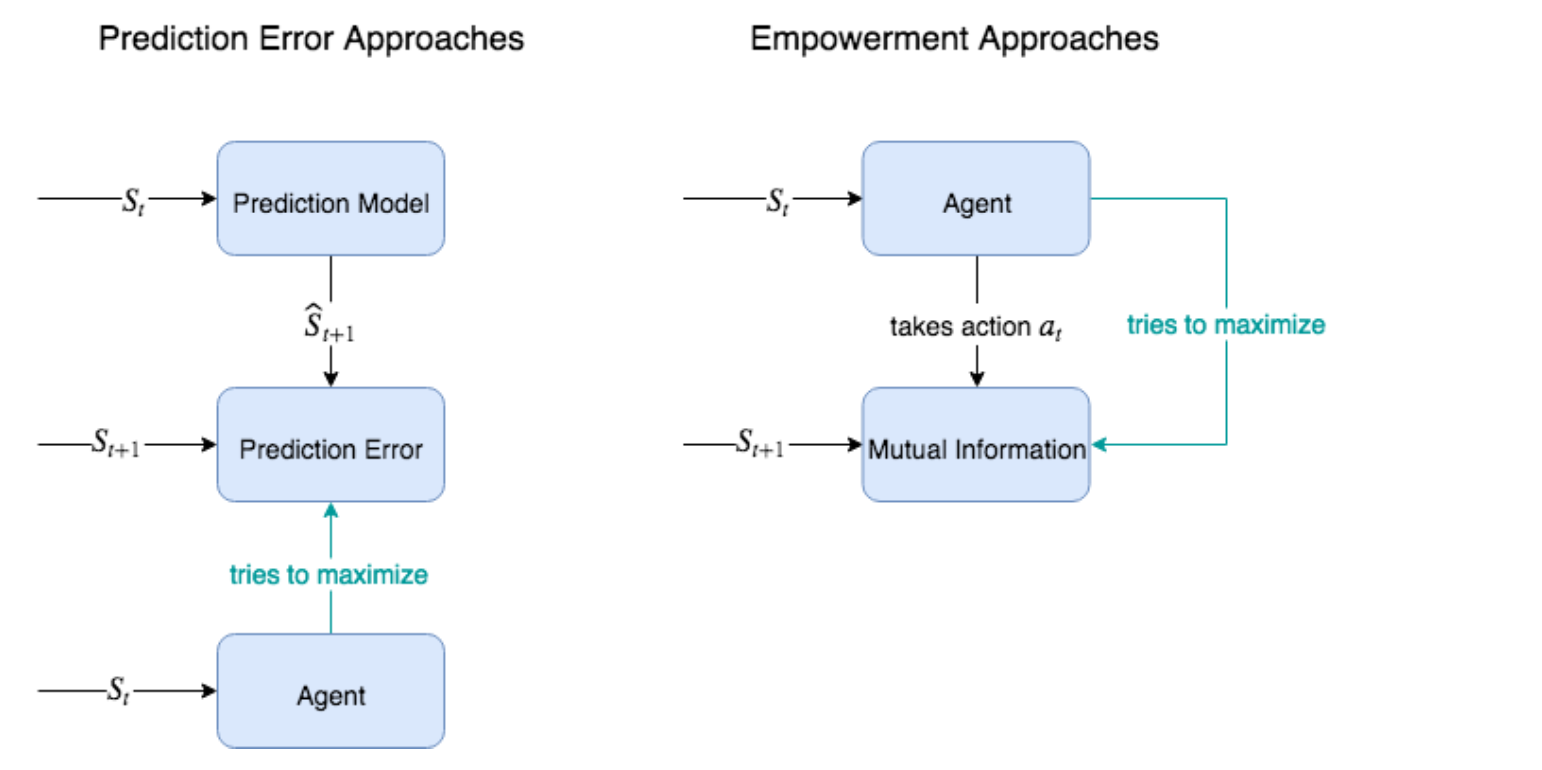
Figure 8.21 : 호기심과 유사한 방법으로 희소 보상 문제를 해결하기 위한 두 가지 주요 접근 방식은 이 장에서 사용한 것과 같은 예측 오류 방법과 권한 부여 방법이다. 특정 State와 다음 예측 State 사이의 예측 오류를 최대화하려는 것이 아니라 권한 부여 방법으로 에이전트의 Action과 다음 State 간의 상호 정보(MI, Mutual Information)를 최대화하는 것이 목표이다. 에이전트의 Action과 다음 State 사이의 MI가 높으면 에이전트가 다음 State에 대해 높은 수준의 제어(또는 권한)를 가짐을 의미한다. 즉, 에이전트가 어떤 Action을 수행했는지 알면 다음을 잘 예측할 수 있다. 이는 에이전트가 환경을 최대한 제어하는 방법을 학습하도록 한다.

기본 전제는 상호 정보(Mutual Information)라는 수량에 의존한다. 여기서는 수학적으로 정의하지는 않지만 비공식적으로 상호 정보(MI)는 확률 변수(Random Variable)라고 하는 두 데이터 소스간에 공유되는 정보의 양을 측정한다(일반적으로 임의의 무작위 또는 불확실성이 있는 데이터를 처리하기 때문에). 덜 체계적인 또다른 정의는 MI를 한 수량 x에 대한 불확실성이 다른 수량 y로 줄어드는 정도를 측정한다 고 정의한다.

정보 이론은 실제 통신 문제를 염두에 두고 처음 개발되었으며, 잡음이 많은 통신 채널에서 메시지를 잘 인코딩하여 수신된 메시지가 손상되지 않도록 하는 방법을 연구했다. 잡음이 있는 통신 회선(예 : 회선으로 전파를 사용함)을 통해 보내려는 원래 메시지 x를 가지고 있으며 x와 수신된 메시지 사이의 상호 정보(MI)를 최대화하고자 한다. 예를 들어, 잡음에 의해 데이터가 손상될 가능성을 최소화하는 전파 패턴으로 생성된 텍스트 문서가 한 사례이다. 따라서 다른 사람이 해독 된 메시지 y를 받으면 수신 된 메시지가 원본 메시지와 매우 가깝다는 것을 확신 할 수 있다.

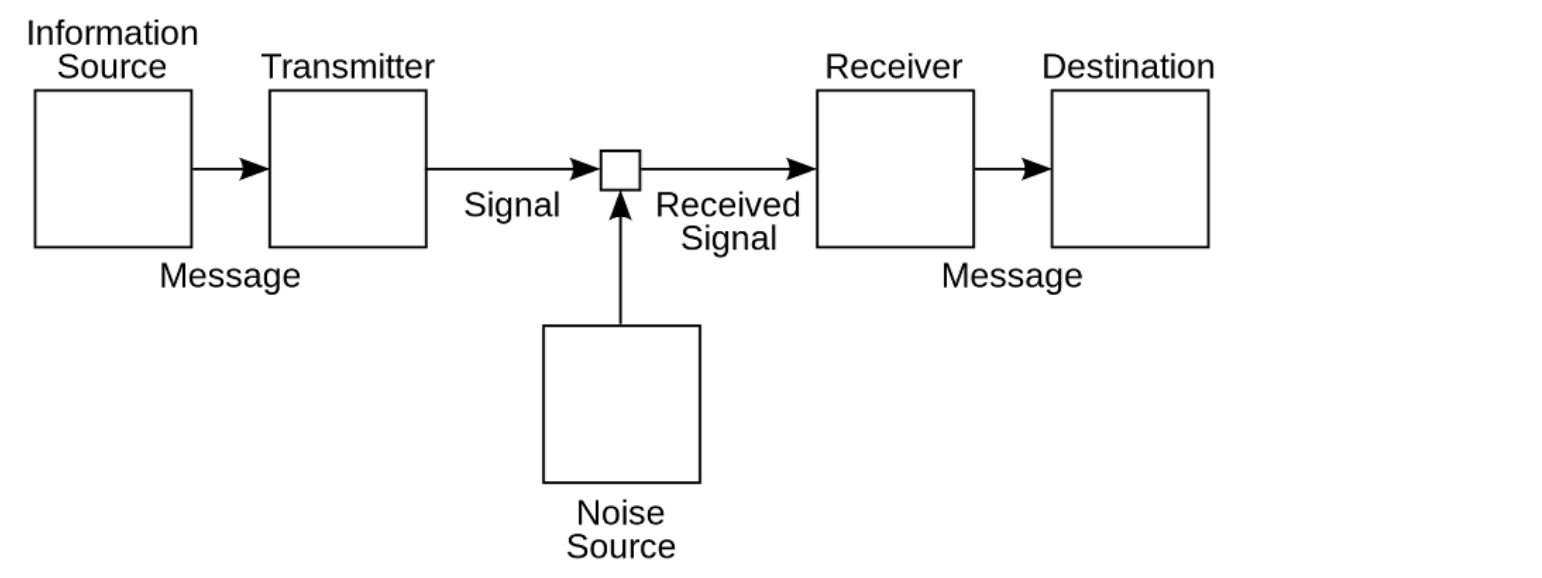
Figure 8.22: Claude Shannon은 설명된 것처럼 잡음이 많은 통신 채널에서 메시지를 효율적이고 강력하게 인코딩할 필요성에 의해 통신 이론을 개발했다. 수신된 메시지와 전송된 메시지 사이의 상호 정보가 최대가 되도록 메시지를 인코딩하는 것이 목표이다.

앞 예에서 x와 y는 모두 일종의 서면 메시지(written message)였지만 x와 y는 같은 유형의 양(quantity)일 필요는 없다. 예를 들어, 회사의 1년 주가 이력과 연간 수익간에 상호 정보가 무엇인지 물어볼 수 있다. 즉, 회사의 연간 매출에 대해서는 매우 불확실한 추정치로 시작한 다음 1년의 주가 이력을 학습할 경우, 불확실성이 얼마나 줄어 들까요? 많이 줄이면 MI가 높다. 이 둘은 양(quantity)의 유형이 다르지만 둘 다 달러 단위를 사용하고 있다. 심지어 단위가 같아야할 필요도 없다. 예를 들어, 온도와 아이스크림 가게의 판매량 사이에 상호 정보가 무엇인지 물어볼 수 있다.

강화 학습에서 에이전트 권한 부여의 경우, 목표는 Action(또는 Action 순서)와 결과적인 미래 State 사이의 상호 정보를 최대화하는 것이다. 이 목표를 최대화하면 에이전트가 수행한 Action을 알면 결과 State에 대한 확신이 높아진다. 즉, 에이전트는 해당 Action이 주어진 State에 안정적으로 도달 할 수 있기 때문에 환경에 대한 높은 수준의 제어 권한을 갖는다. 따라서 최대 권한을 부여한 에이전트는 최대 자유도를 갖는다.

PE를 최소화하면 직접적으로 탐험(Exploration)을 장려(Encourage)하는 반면, 권한 부여를 최대화하면 권한을 부여하는 기술(Behavior)을 학습하기 위한 수단으로 탐험적 Action을 유도할 수 있지만 간접적으로만 가능하다. 세상을 여행하여 가능한한 많이 탐험을 하고 있는 젊은 여성 사라가 있다고 생각해 보자. 사라는 세상에 대한 불확실성을 줄이고 있다. 그녀를 높은 수준의 파워를 가진 빌 게이츠 (Bill Gates)와 비교해 보면, 빌게이츠는 사라만큼 여행에 관심이 없을 수도 있지만, 원한다면 언제 어디로 가든 가고 싶은 곳으로 갈 수 있다.

권한 부여와 호기심은 둘 모두 사용 사례가 있다. 권한 부여 기반(Empowerment-based) 목적은 학습 에이전트가 외적 보상(예 : 로봇 작업 또는 스포츠 게임)없이 복잡한 기술을 습득하는 데 유용한 것으로 나타났다. 호기심 기반(Curiosity-based) 목적은 탐험(Exploration)에 더 유용한 경향이 있다 (예 : Super Mario Bros. 목표는 레벨을 진행하는 것이다). 어쨌든 이 두 메트릭은 서로 유사하다.

8.8 Summary

• 이 장에서는 희소 보상 문제를 살펴보고 이를 해결하기 위한 기술에 대해 배웠다.
• 우리는 DQN(Deep Q-network) 에이전트를 구현하고 본질적 호기심 모듈(ICM, Intrinsic Curiosity Module)과 페어링했다.
• 본질적 호기심 모듈(ICM, Intrinsic Curiosity Module)은 3개의 독립적인 신경망으로 구성된다 : 순방향 모델, 인버스 모델, 인코더.
• 인코더는 고차원 상태를 고차원 특징을 갖는 저차원 벡터로 인코딩한다(잡음 및 사소한 특징 제거).
• 순방향 모델은 다음 인코딩된 State를 예측하고 그 오류는 호기심 신호(Curiosity Signal)를 제공한다.
• 인버스 모델은 두 개의 연속된 인코딩 State를 취하고 수행된 Action을 예측하여 인코더를 학습시킨다.
• 우리는 강화 학습 에이전트의 본질적 동기(Intrinsic motivation)의 하위 분야에 대해 배웠고 ICM의 대안으로 권한 부여 접근법(Empowerment approach)에 대해 논의했다.