DRL Dynamic Programming

from IPython.display import Image
Image(filename='./images/1-0-0-1_opening.jpg')

Lesson 1-3: Dynamic Programming

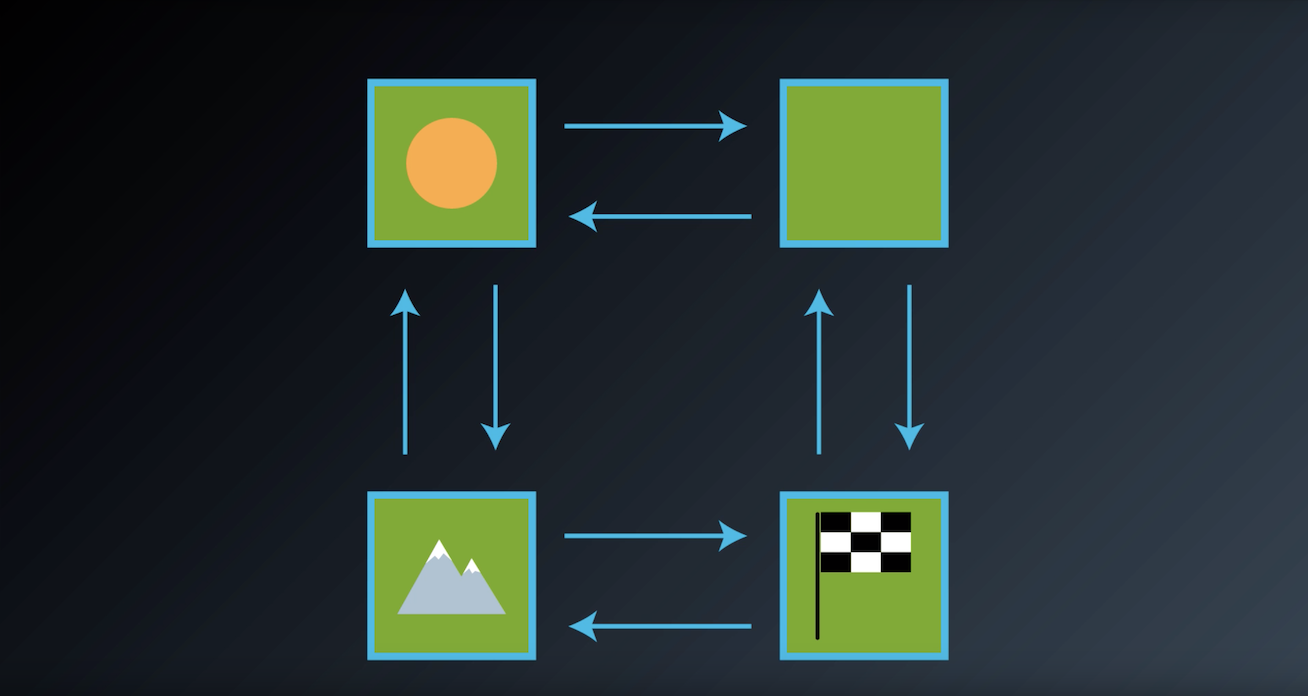
In the dynamic programming setting, the agent has full knowledge of the Markov decision process (MDP) that characterizes the environment. (This is much easier than the reinforcement learning setting, where the agent initially knows nothing about how the environment decides state and reward and must learn entirely from interaction how to select actions.)

This lesson covers material in Chapter 4 (especially 4.1-4.4) of the Sutton’s textbook.

1-3-1 : Grid Example

from IPython.display import Image
Image(filename='./images/1-3-1-1_grid_example.png')

from IPython.display import Image
Image(filename='./images/1-3-1-2_grid_example.png')

from IPython.display import Image
Image(filename='./images/1-3-1-3_grid_example.png')

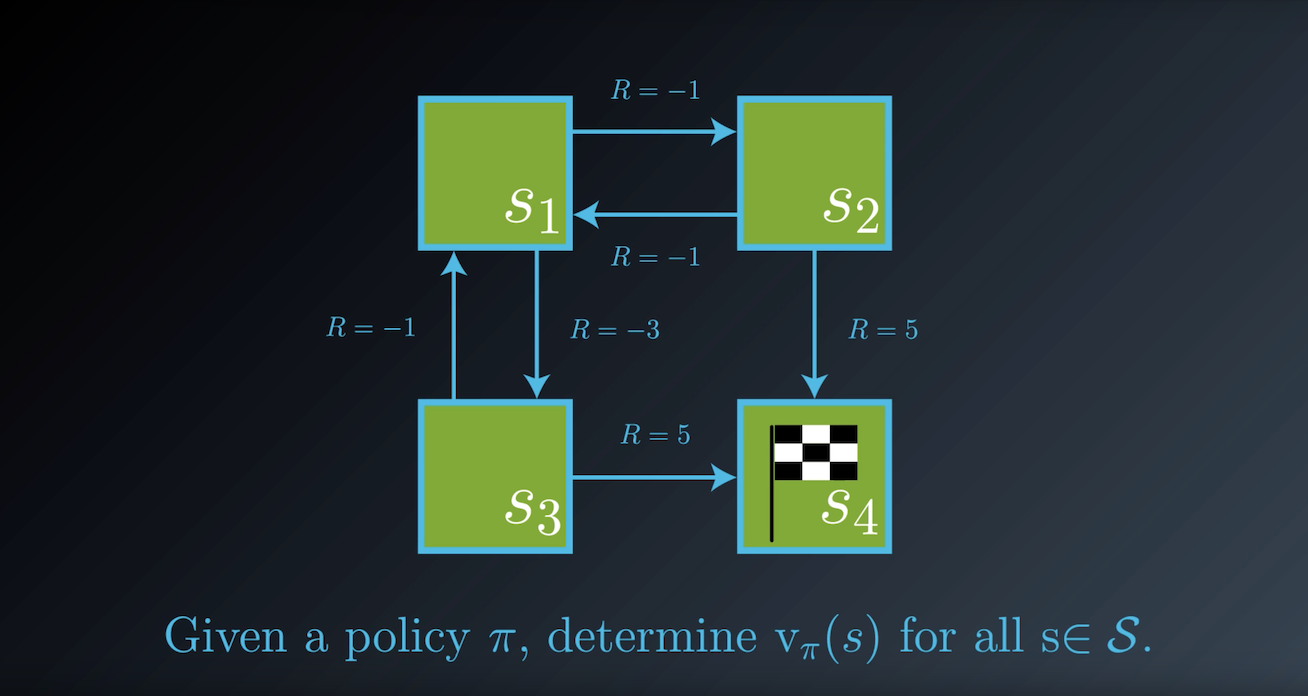
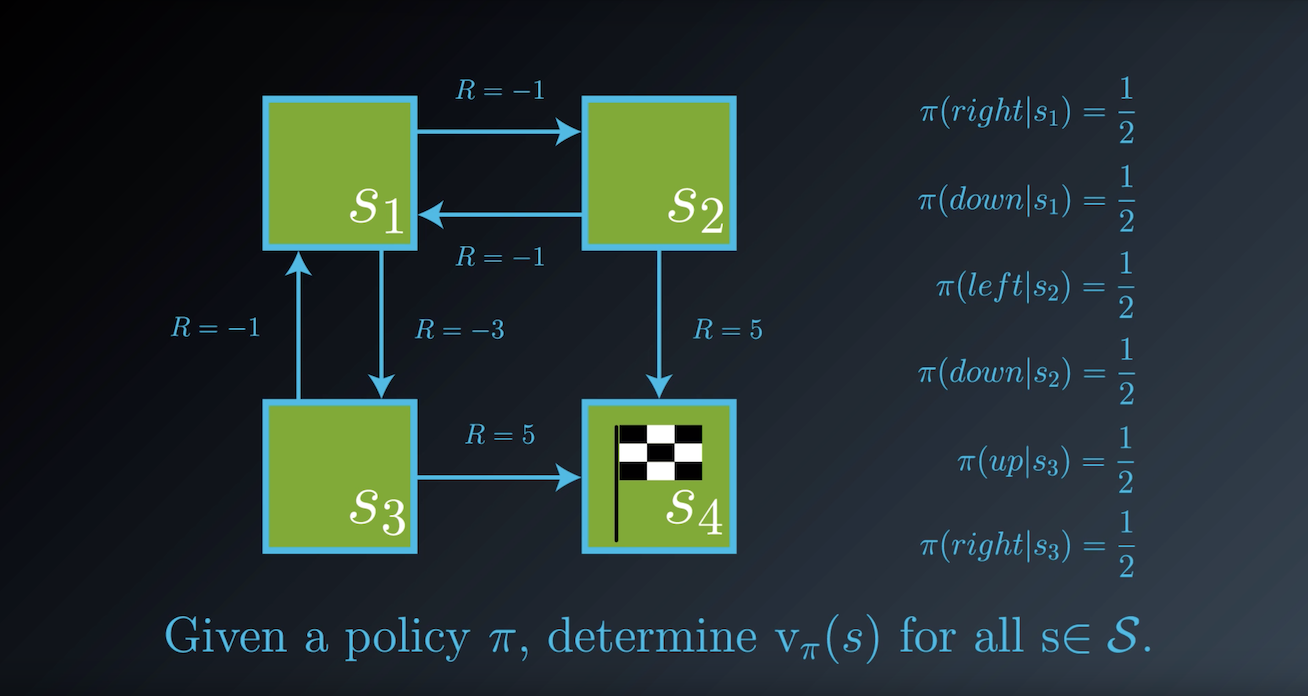
1-3-2 : Iterative Method

from IPython.display import Image
Image(filename='./images/1-3-2-1_dp_iterative_method_step1.png')

from IPython.display import Image
Image(filename='./images/1-3-2-2_dp_iterative_method_step2.png')

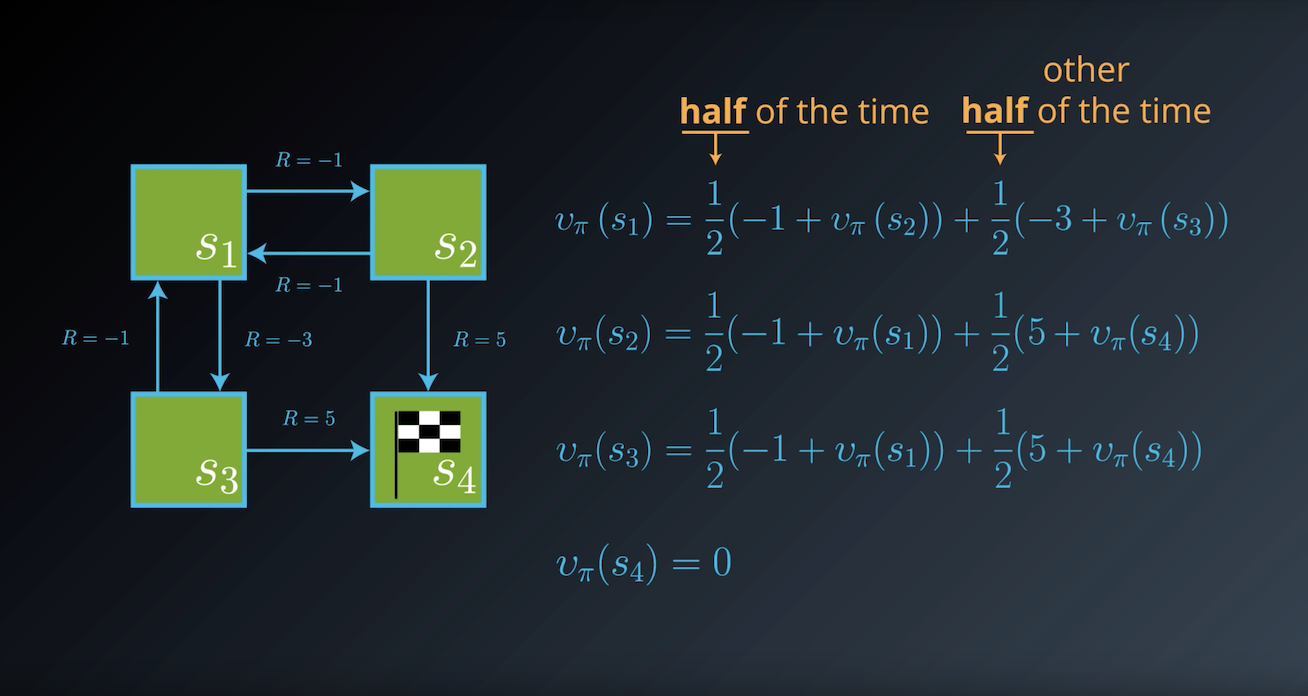
from IPython.display import Image
Image(filename='./images/1-3-2-3_dp_iterative_method_step3.png')

from IPython.display import Image
Image(filename='./images/1-3-2-4_dp_iterative_method_step4.png')

from IPython.display import Image
Image(filename='./images/1-3-2-5_dp_iterative_method_step5.png')

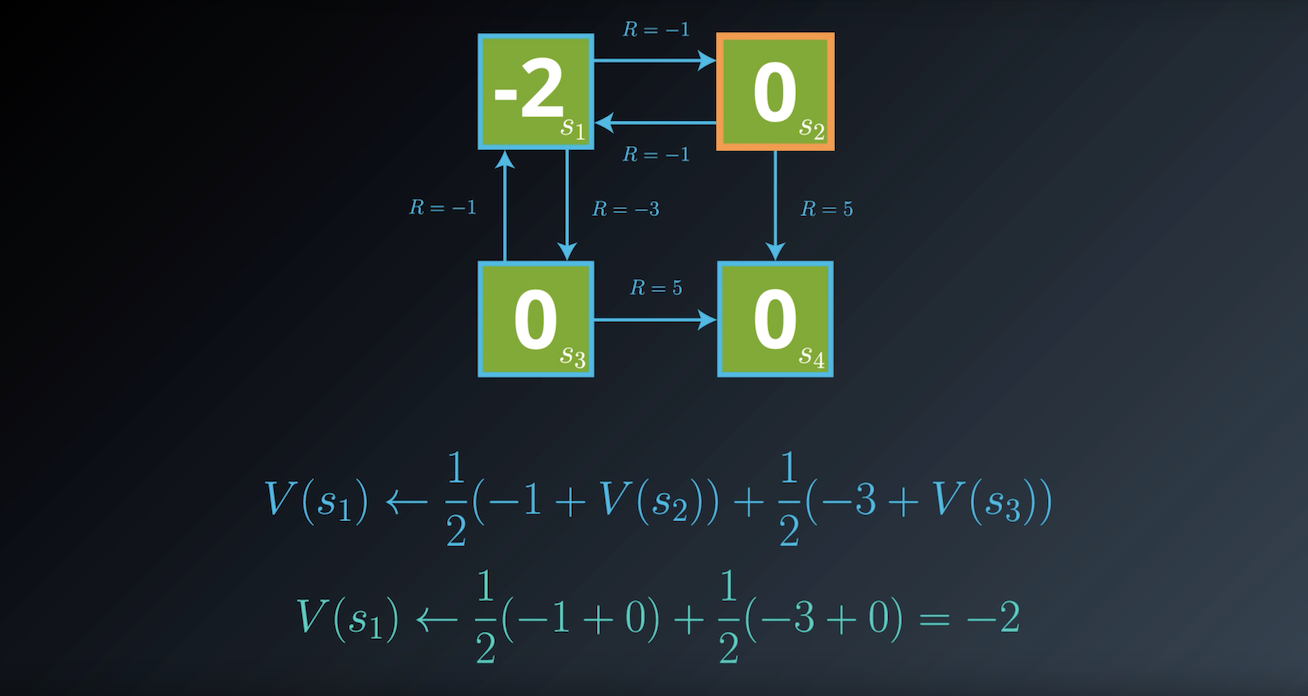
from IPython.display import Image
Image(filename='./images/1-3-2-6_dp_iterative_method_step6.png')

from IPython.display import Image
Image(filename='./images/1-3-2-7_dp_iterative_method_step7.png')

from IPython.display import Image
Image(filename='./images/1-3-2-8_dp_iterative_method_step8.png')

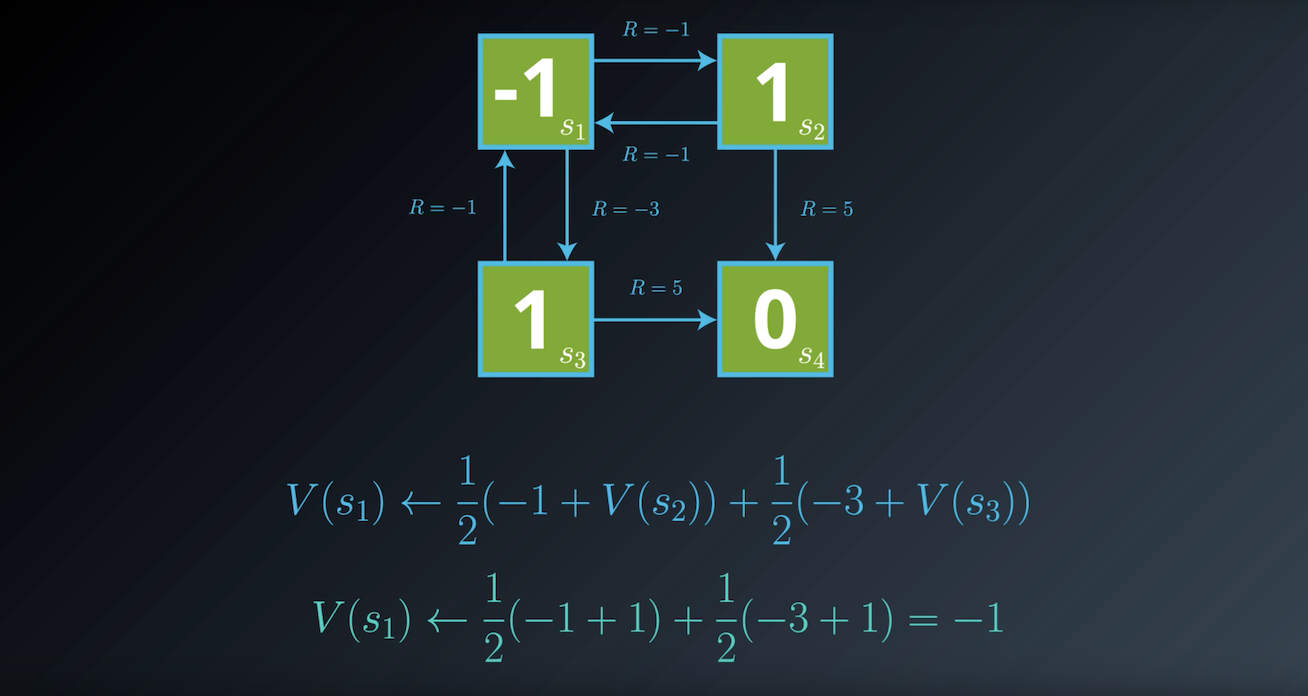
Notes on the Bellman Expectation Equation

In the previous example, we derived one equation for each environment state. For instance, for state s1 we saw that:

from IPython.display import Image
Image(filename='./images/1-3-2-9_dp_iterative_method_Notes_on_the_Bellman_Expectation_Equation.png')

from IPython.display import Image
Image(filename='./images/1-3-2-10_dp_iterative_method_Notes_on_the_Bellman_Expectation_Equation.png')

from IPython.display import Image
Image(filename='./images/1-3-2-11_dp_iterative_method_Notes_on_the_Bellman_Expectation_Equation.png')

Notes on Solving the System of Equations

from IPython.display import Image
Image(filename='./images/1-3-2-12_dp_iterative_method_Notes_on_Solving_the_System_of_Equations.png')

from IPython.display import Image
Image(filename='./images/1-3-2-13_dp_iterative_method_Notes_on_Solving_the_System_of_Equations.png')

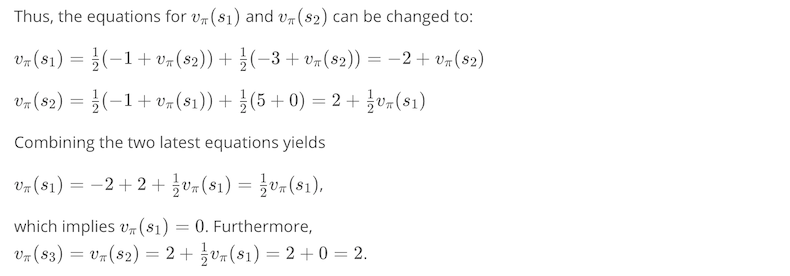
from IPython.display import Image
Image(filename='./images/1-3-2-14_dp_iterative_method_Notes_on_Solving_the_System_of_Equations.png')

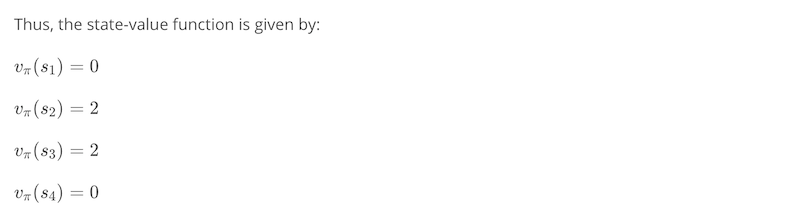
Note : This example serves to illustrate the fact that it is possible to directly solve the system of equations given by the Bellman expectation equation for vπ. However, in practice, and especially for much larger Markov decision processes (MDPs), we will instead use an iterative solution approach.

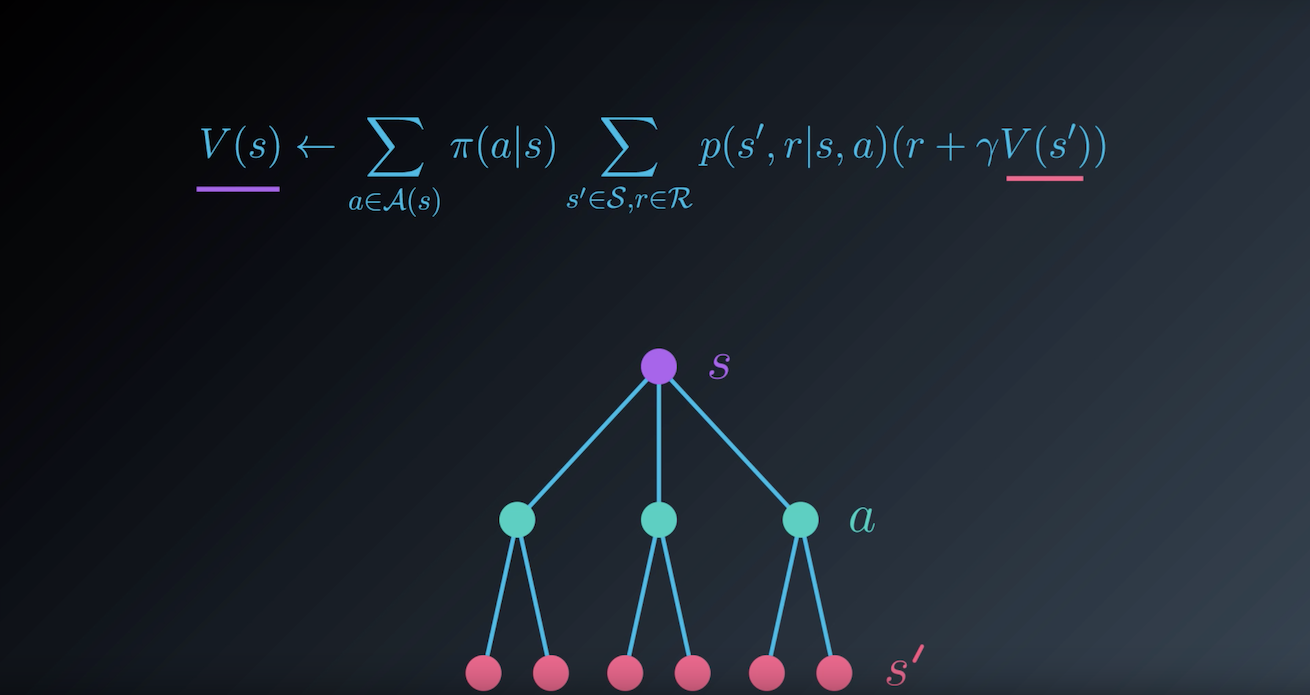
1-3-3. Iterative Policy Evaluation

from IPython.display import Image
Image(filename='./images/1-3-3-1_dp_Iterative-Policy-Evaluation_step1.png')

from IPython.display import Image
Image(filename='./images/1-3-3-2_dp_Iterative-Policy-Evaluation_step2.png')

from IPython.display import Image
Image(filename='./images/1-3-3-3_dp_Iterative-Policy-Evaluation_step3.png')

from IPython.display import Image
Image(filename='./images/1-3-3-4_dp_Iterative-Policy-Evaluation_step4.png')

from IPython.display import Image
Image(filename='./images/1-3-3-5_dp_Iterative-Policy-Evaluation_step5.png')

from IPython.display import Image
Image(filename='./images/1-3-3-6_dp_Iterative-Policy-Evaluation_step6.png')

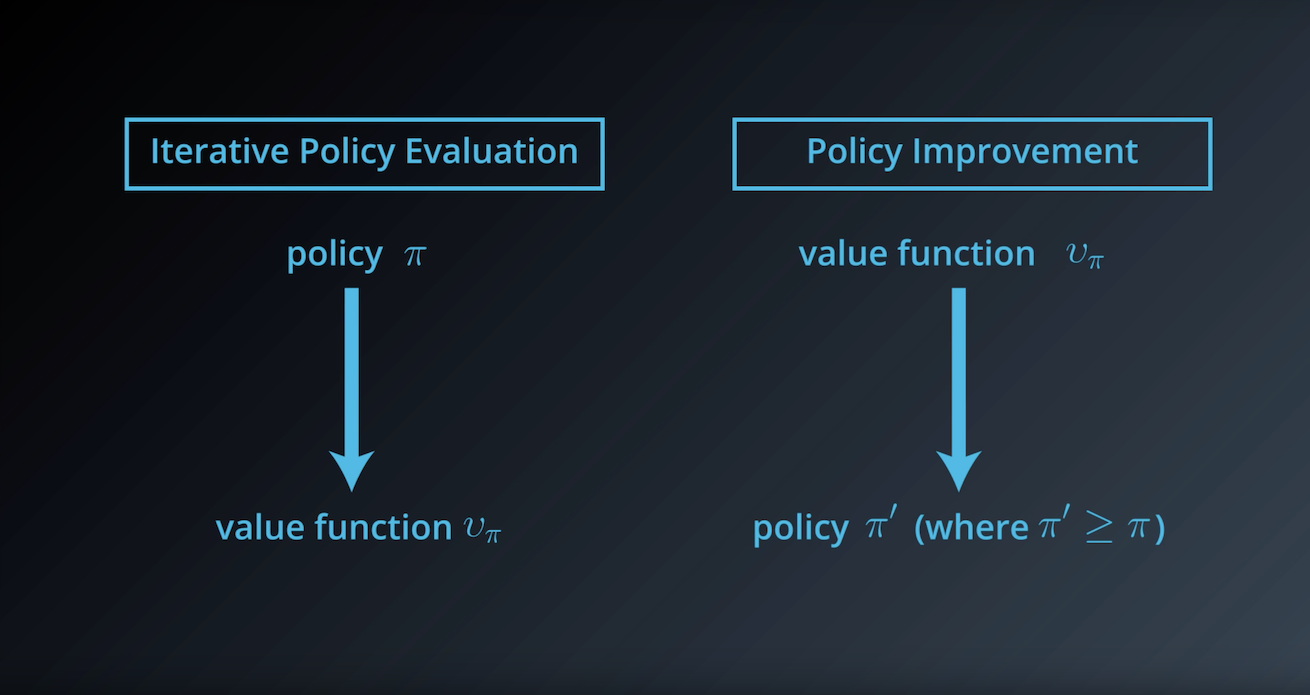
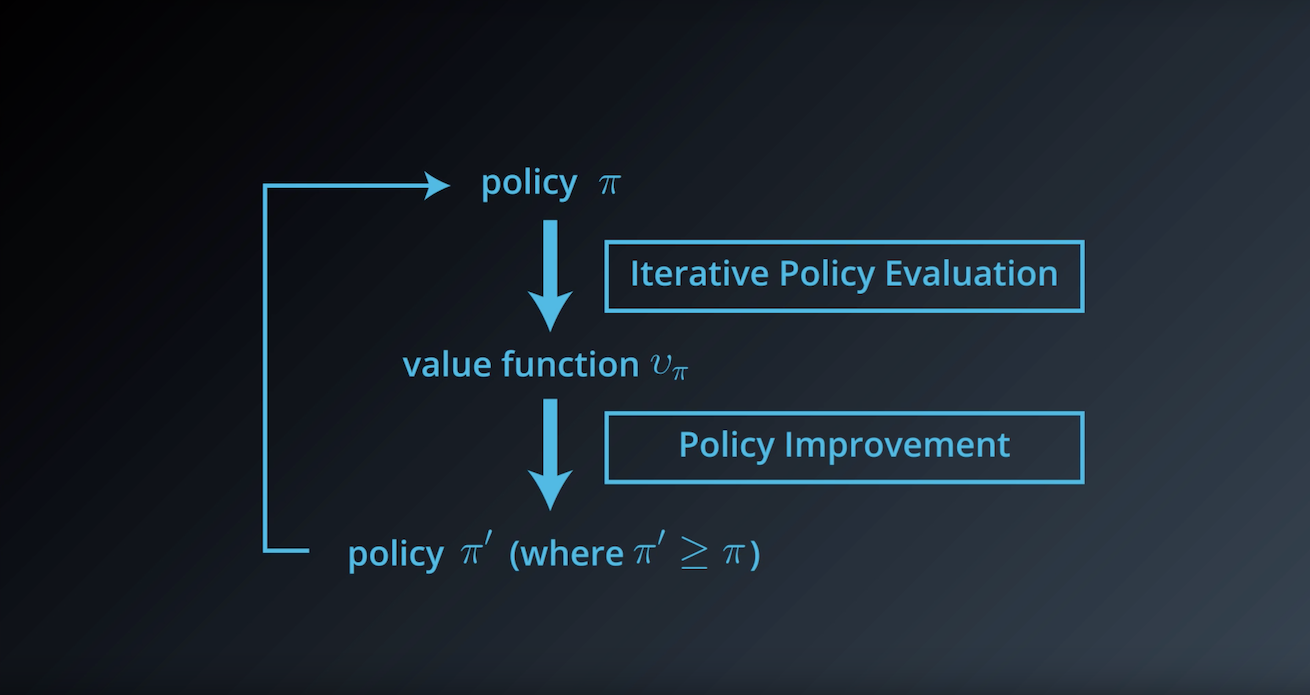
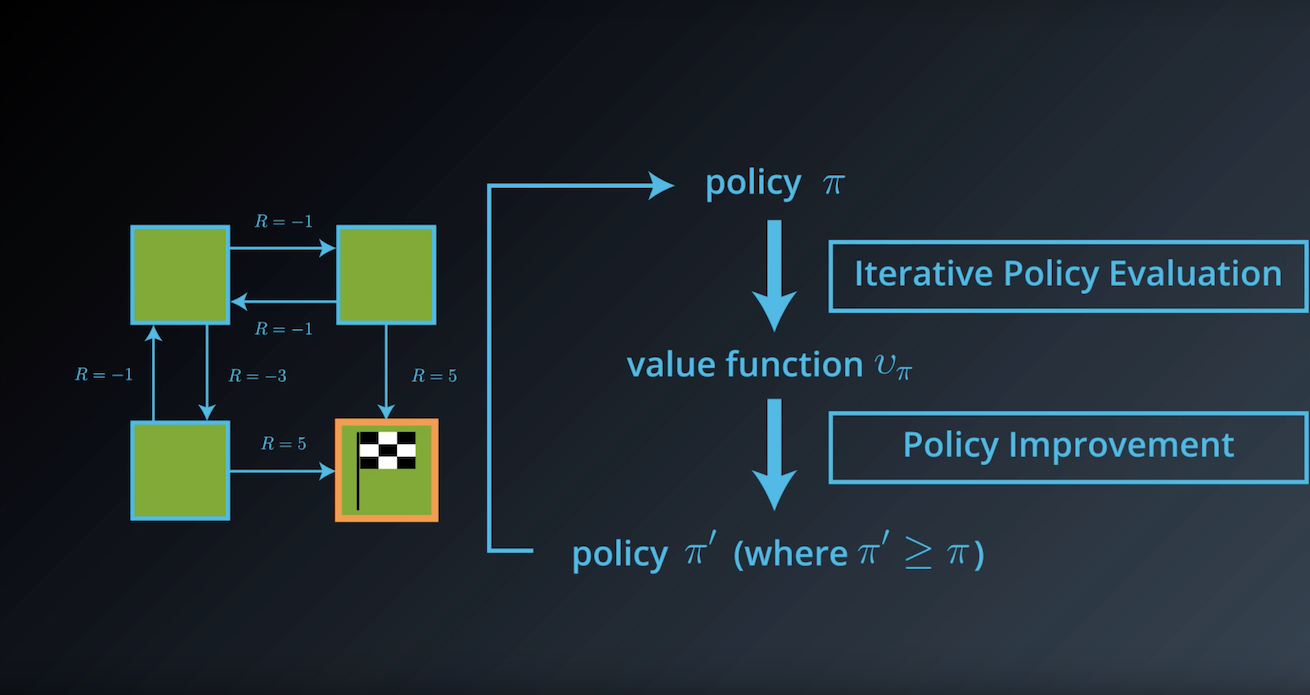
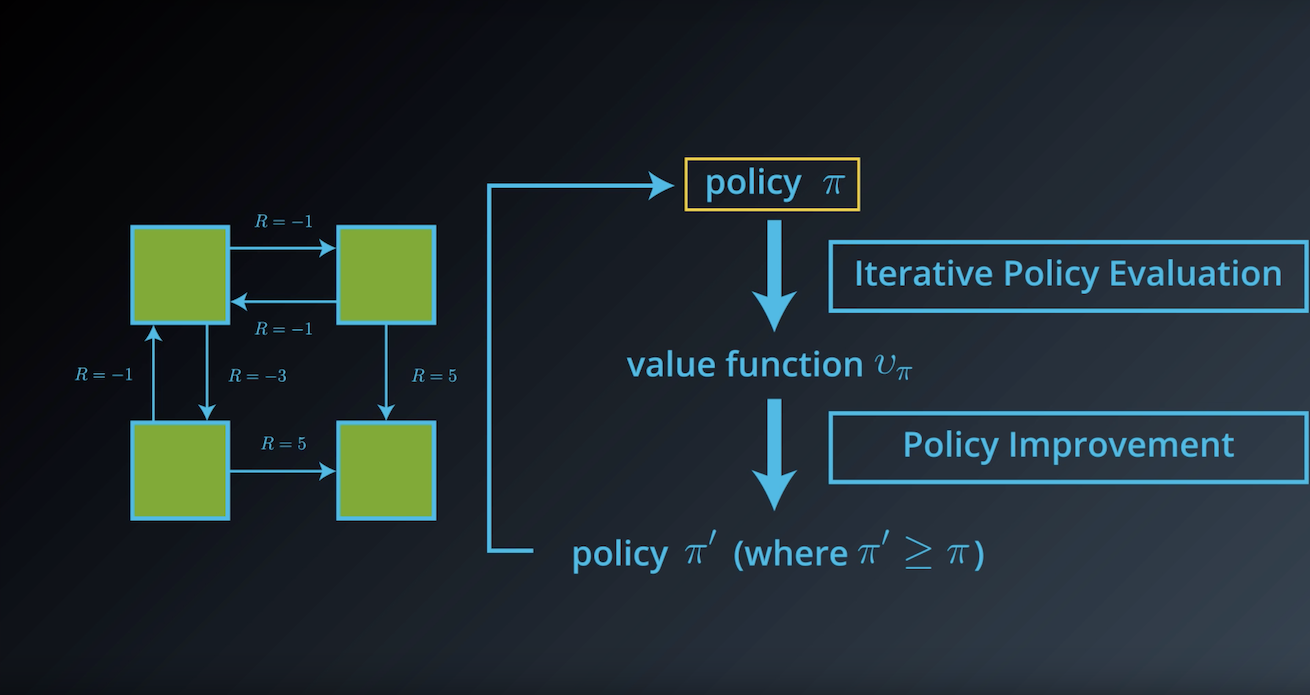
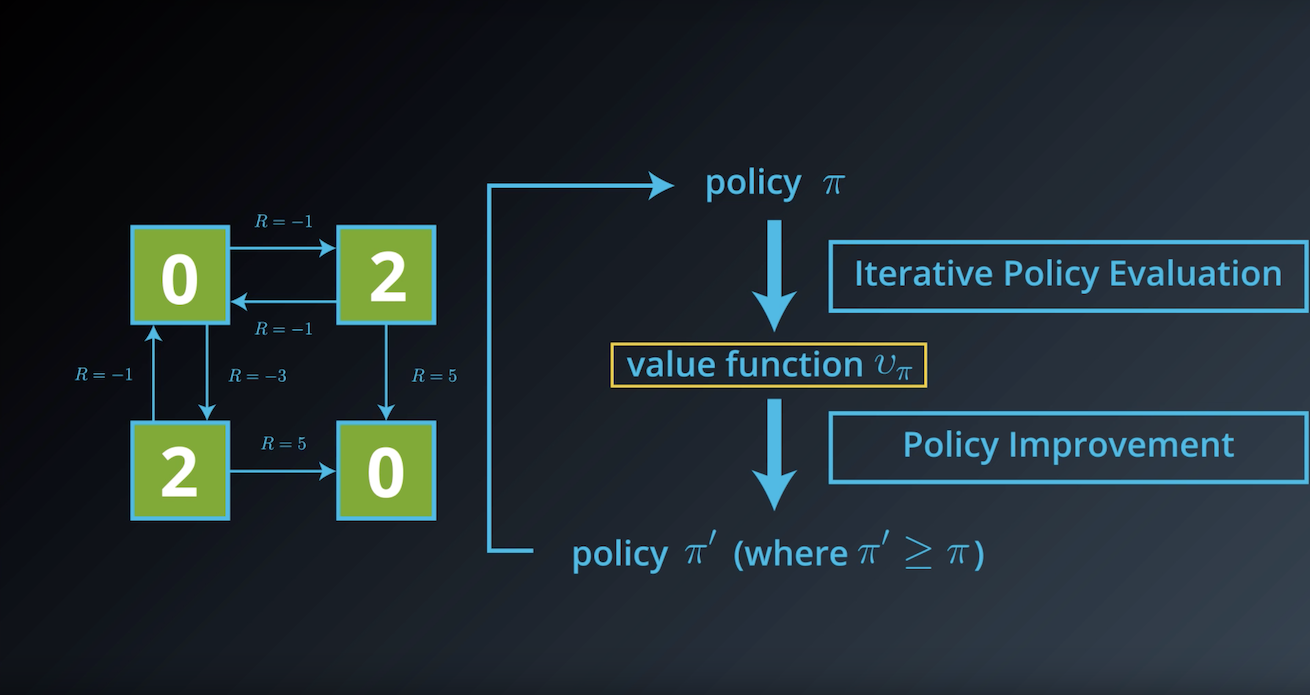
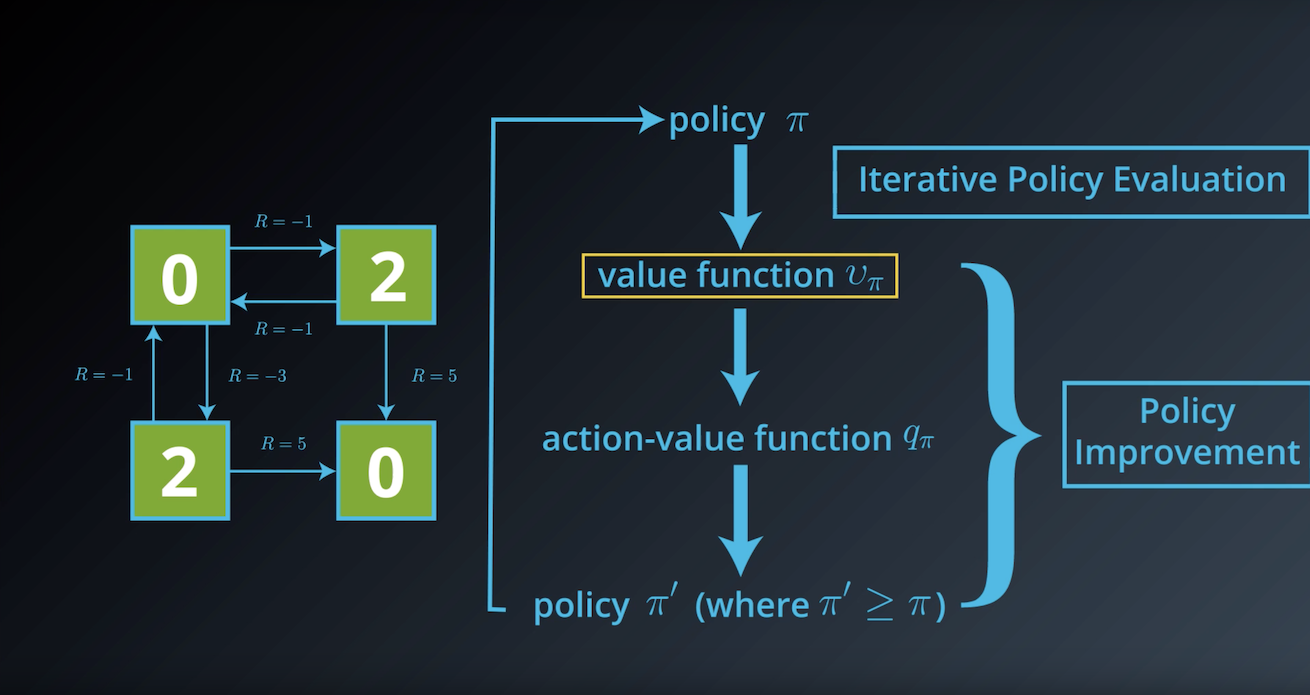
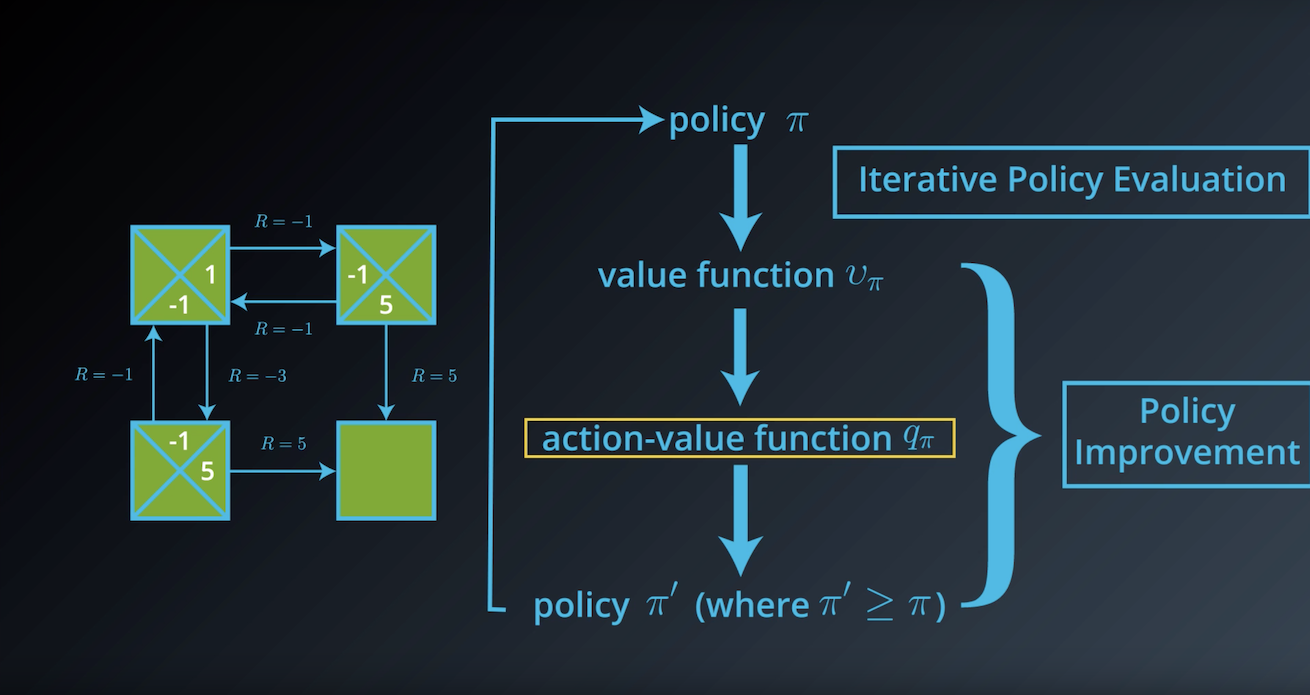
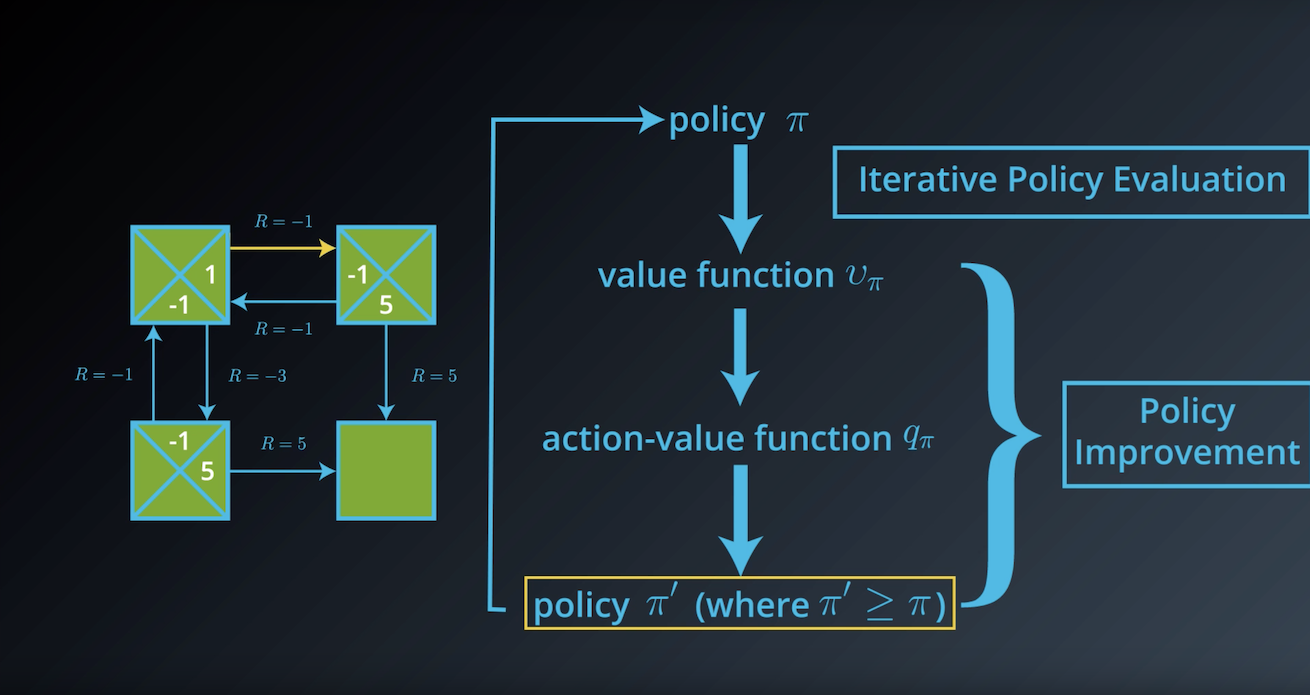
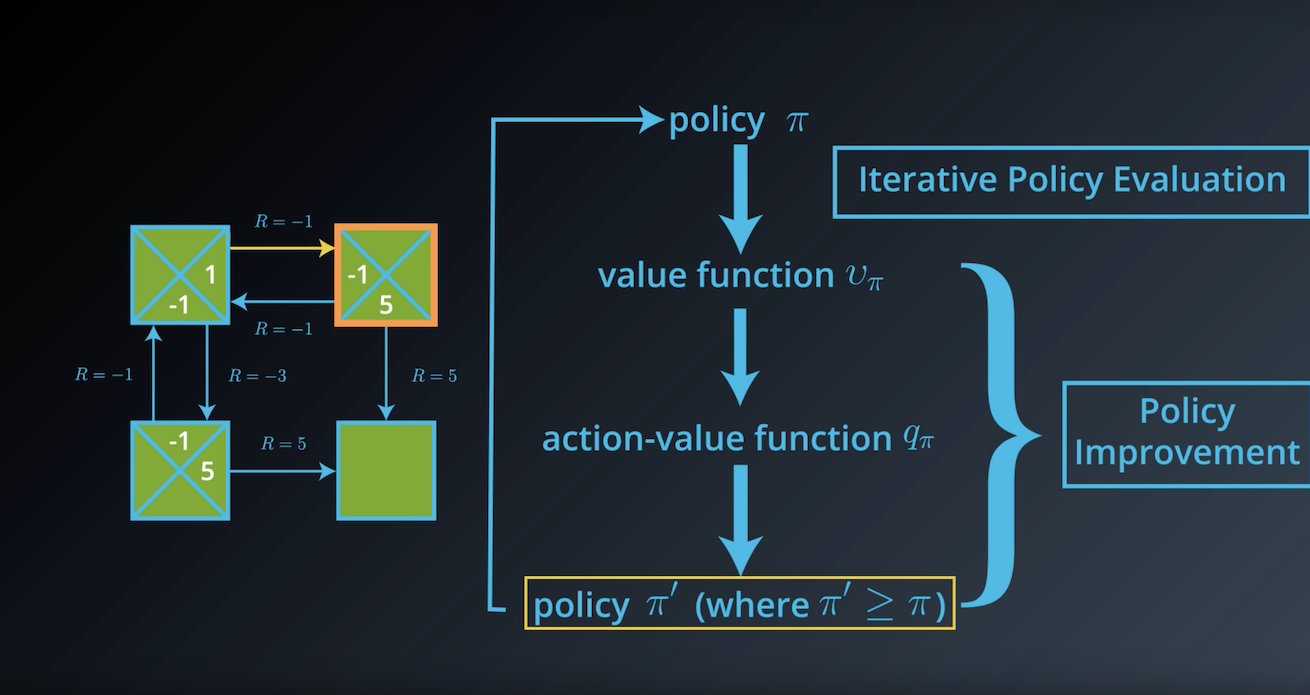
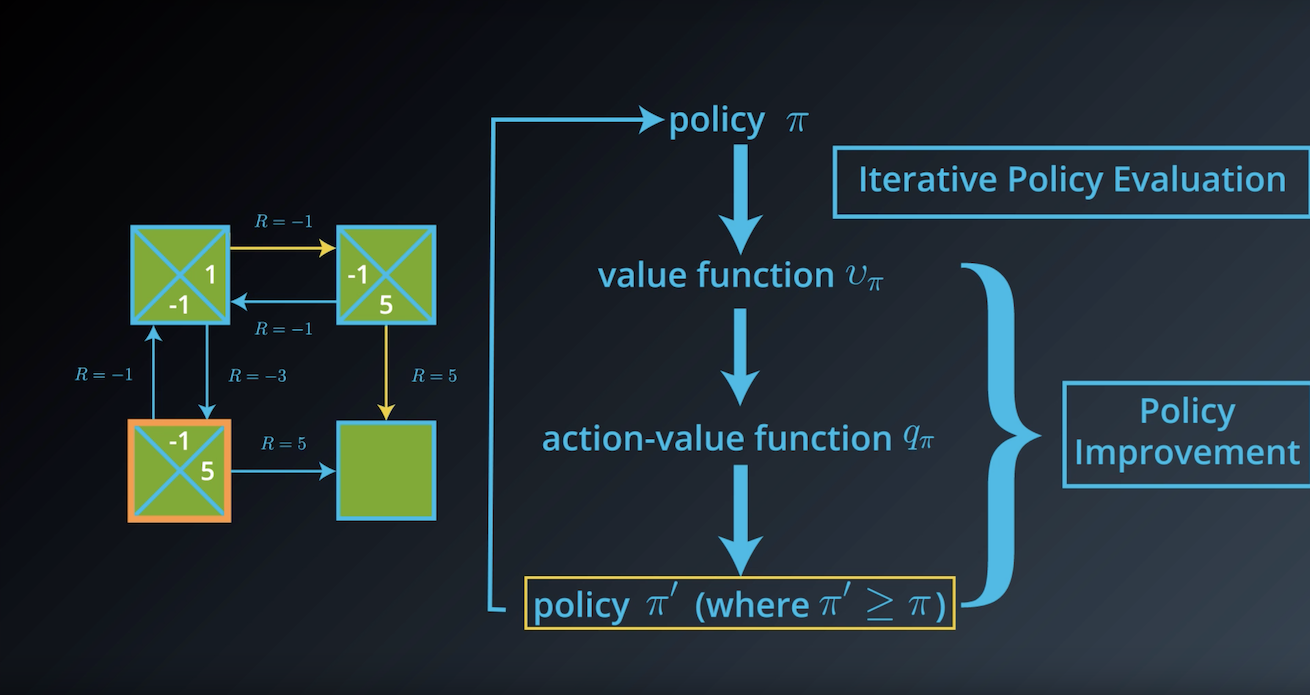
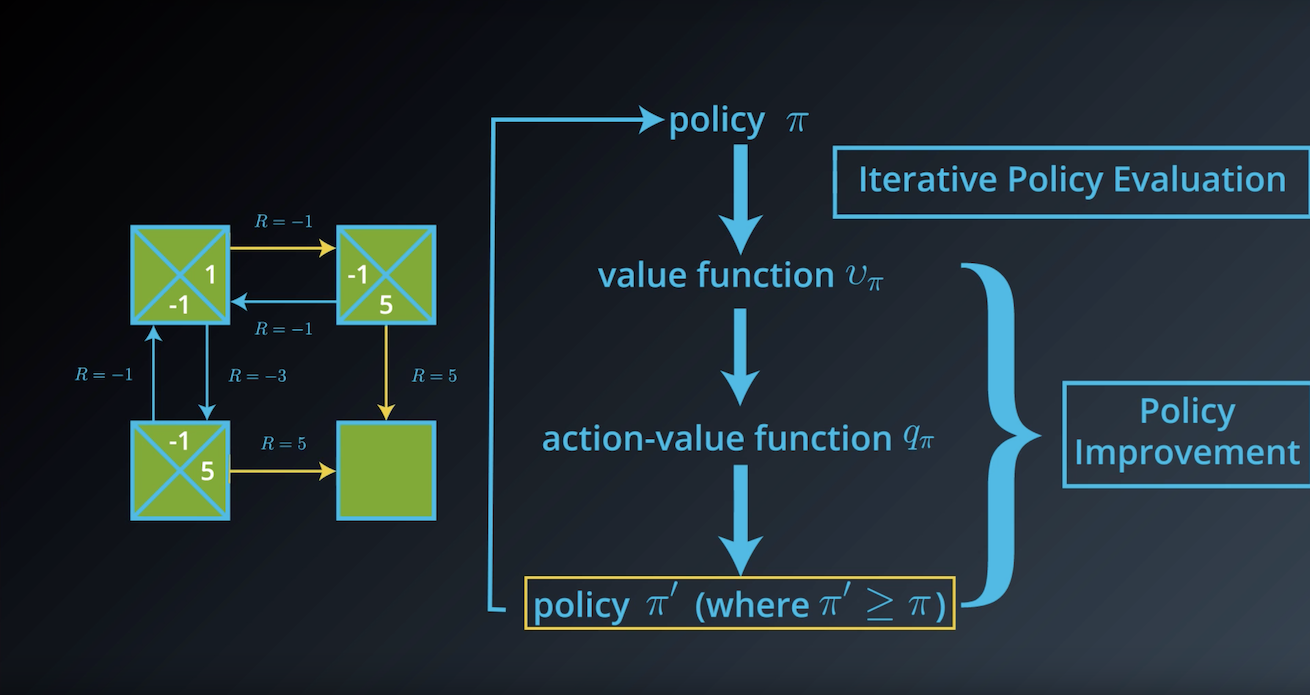
1-3-4 : Policy Improvement

from IPython.display import Image
Image(filename='./images/1-3-4-1_dp_policy_evaluation_step1.png')

from IPython.display import Image
Image(filename='./images/1-3-4-2_dp_policy_evaluation_step2.png')

from IPython.display import Image
Image(filename='./images/1-3-4-3_dp_policy_evaluation_step3.png')

from IPython.display import Image
Image(filename='./images/1-3-4-4_dp_policy_evaluation_step4.png')

from IPython.display import Image
Image(filename='./images/1-3-4-5_dp_policy_evaluation_step5.png')

from IPython.display import Image
Image(filename='./images/1-3-4-6_dp_policy_evaluation_step6.png')

from IPython.display import Image
Image(filename='./images/1-3-4-7_dp_policy_evaluation_step7.png')

from IPython.display import Image
Image(filename='./images/1-3-4-8_dp_policy_evaluation_step8.png')

from IPython.display import Image
Image(filename='./images/1-3-4-9_dp_policy_evaluation_step9.png')

from IPython.display import Image
Image(filename='./images/1-3-4-10_dp_policy_evaluation_step10.png')

from IPython.display import Image
Image(filename='./images/1-3-4-11_dp_policy_evaluation_step11.png')

from IPython.display import Image
Image(filename='./images/1-3-4-12_dp_policy_evaluation_step12.png')

from IPython.display import Image
Image(filename='./images/1-3-4-13_dp_policy_evaluation_step13.png')

from IPython.display import Image
Image(filename='./images/1-3-4-14_dp_policy_evaluation_step14.png')

from IPython.display import Image
Image(filename='./images/1-3-4-15_dp_policy_evaluation_step15.png')

from IPython.display import Image
Image(filename='./images/1-3-4-16_dp_policy_evaluation_step16.png')

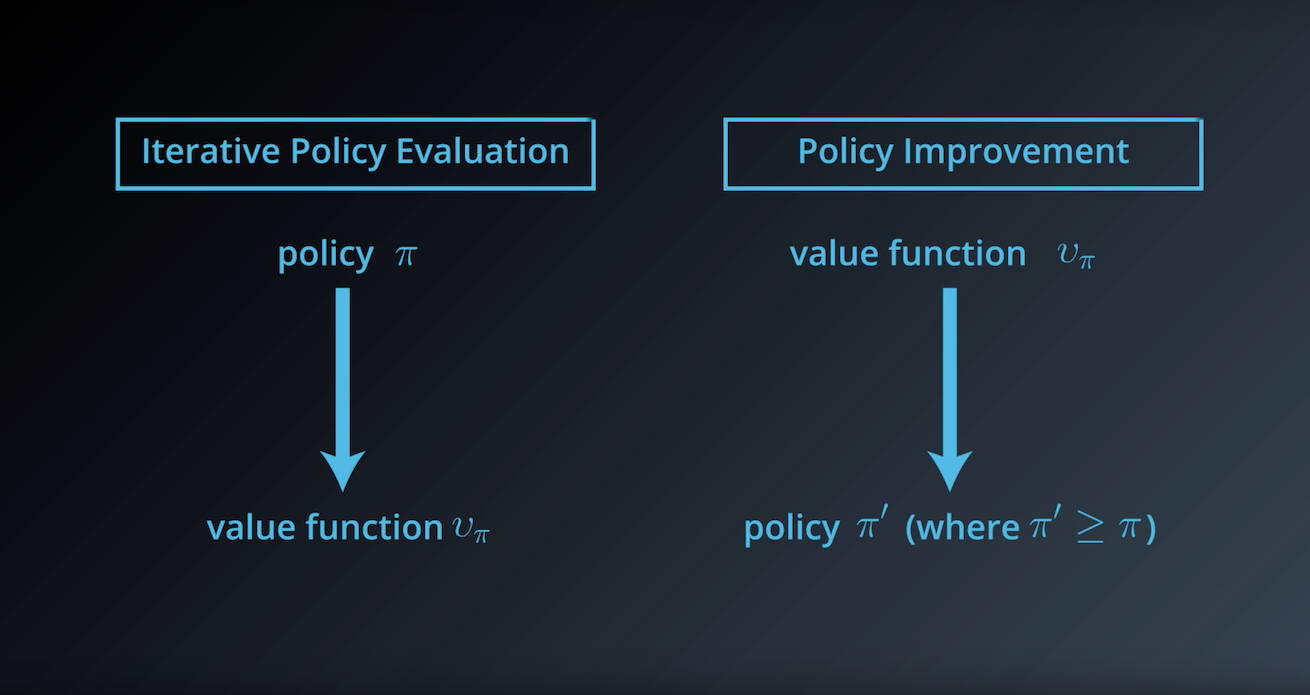
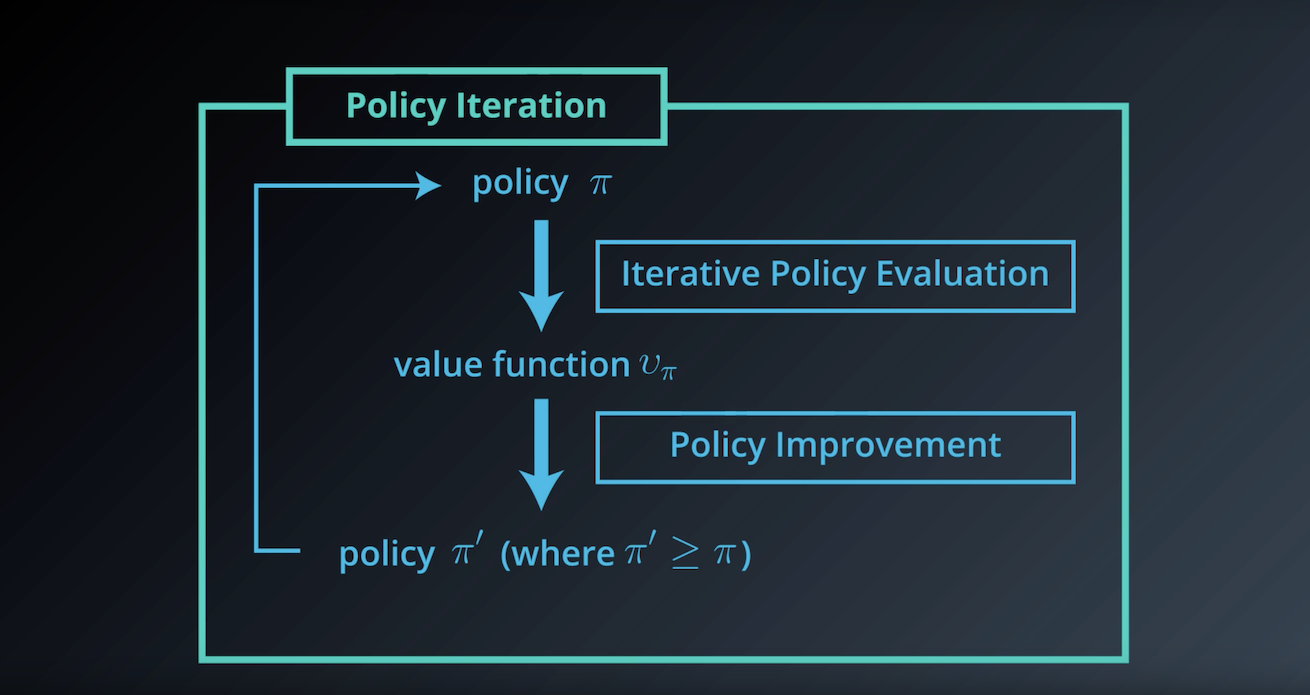
1-3-5 : Policy Iteration

from IPython.display import Image
Image(filename='./images/1-3-5-1_dp_Policy-Iteration_step1.png')

from IPython.display import Image
Image(filename='./images/1-3-5-2_dp_Policy-Iteration_step2.png')

from IPython.display import Image
Image(filename='./images/1-3-5-3_dp_Policy-Iteration_step3.png')

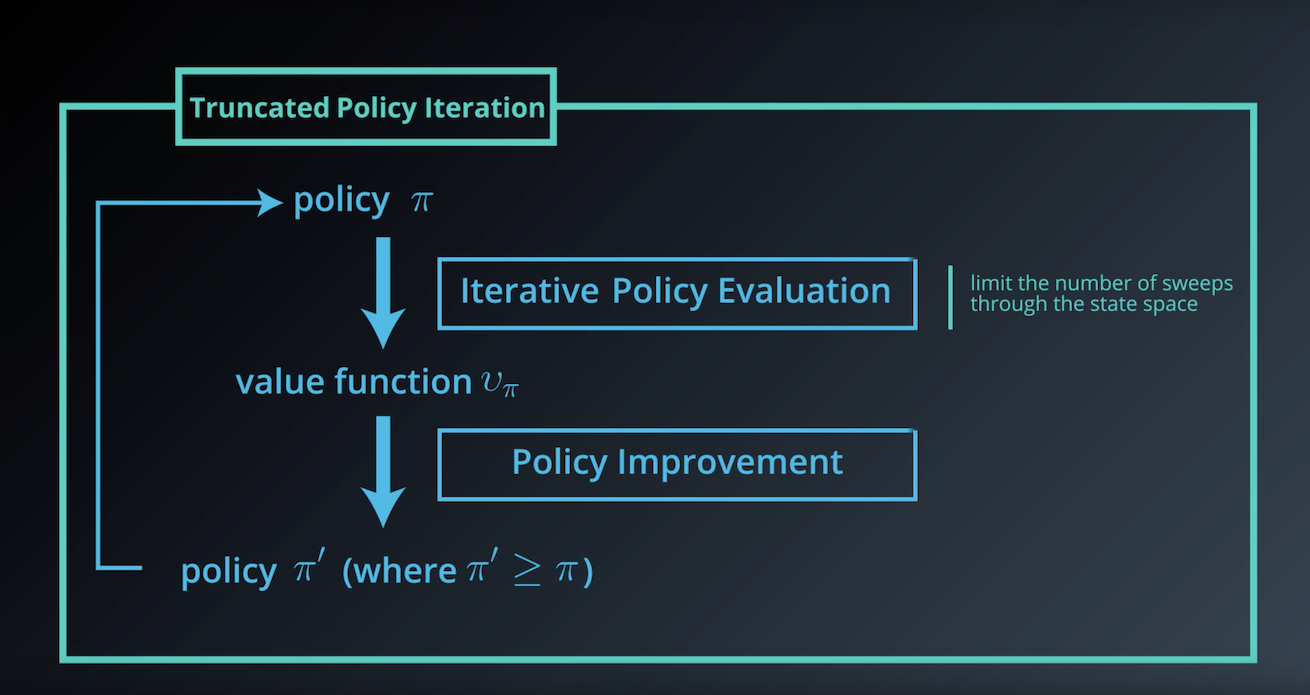
1-3-6 : Truncated Policy Iteration

from IPython.display import Image
Image(filename='./images/1-3-6-1_dp_Truncated-Policy-Iteration_step1.png')

from IPython.display import Image
Image(filename='./images/1-3-6-2_dp_Truncated-Policy-Iteration_step2.png')

from IPython.display import Image
Image(filename='./images/1-3-6-3_dp_Truncated-Policy-Iteration_step3.png')

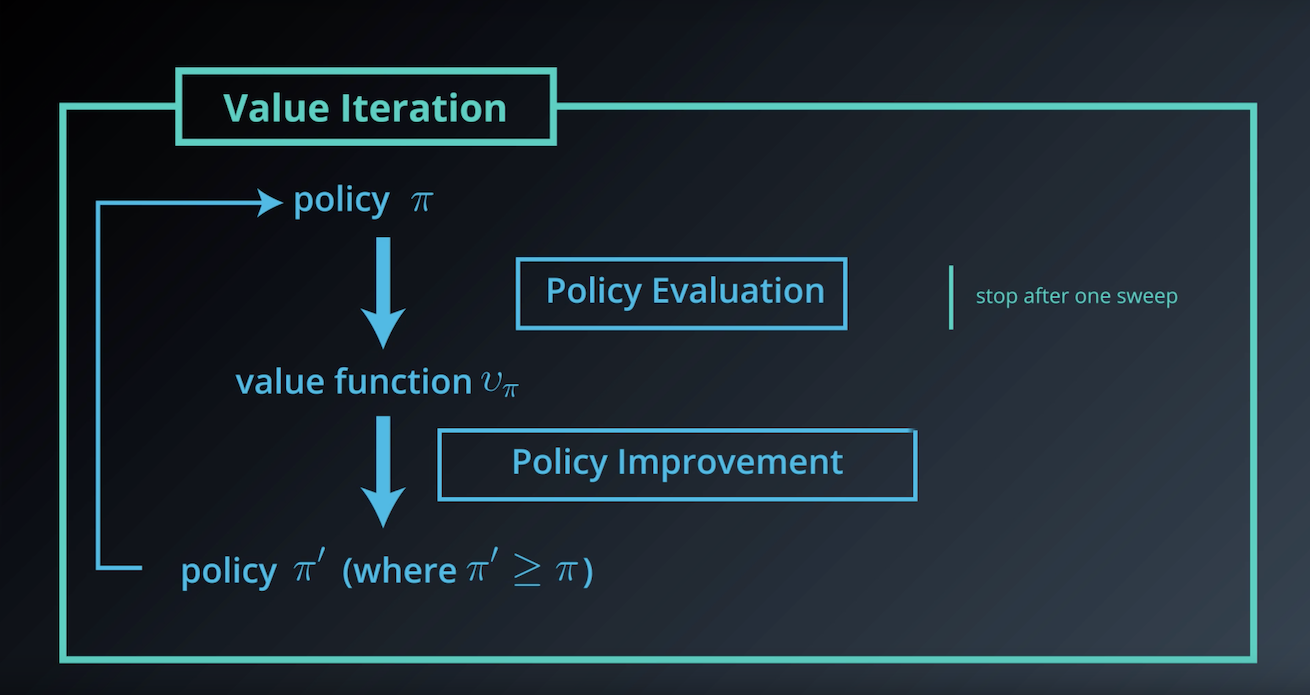
1-3-7 : Value Iteration

from IPython.display import Image
Image(filename='./images/1-3-7-1_dp_Value-Iteration_step1.png')

from IPython.display import Image
Image(filename='./images/1-3-7-2_dp_Value-Iteration_step2.png')

from IPython.display import Image
Image(filename='./images/1-3-7-3_dp_Value-Iteration_step3.png')

from IPython.display import Image
Image(filename='./images/1-3-7-4_dp_Value-Iteration_step4.png')

from IPython.display import Image
Image(filename='./images/1-3-7-5_dp_Value-Iteration_step5.png')

from IPython.display import Image
Image(filename='./images/1-3-7-6_dp_Value-Iteration_step6.png')

from IPython.display import Image
Image(filename='./images/1-3-7-7_dp_Value-Iteration_step7.png')

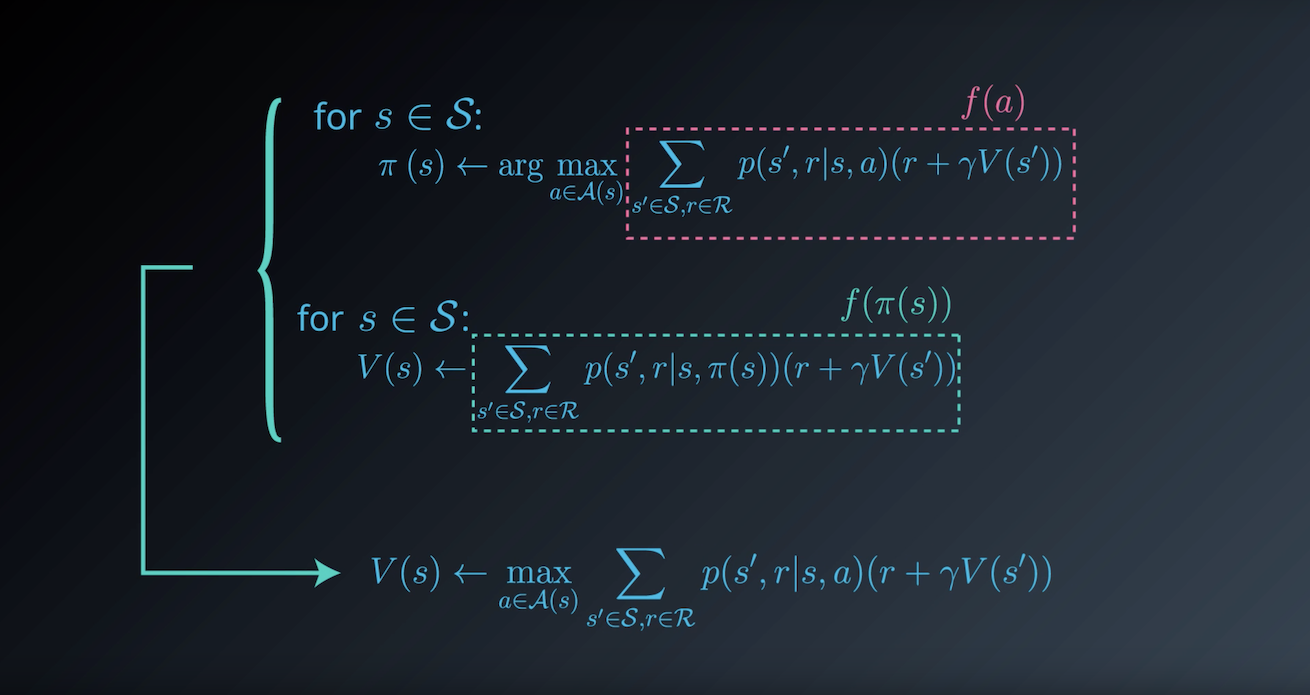
from IPython.display import Image
Image(filename='./images/1-3-7-8_dp_Value-Iteration_step8.png')

1-3-8 : Quiz : Check Your Understanding

Match each algorithm to its appropriate description.

1. Value Iteration
2. Policy Improvement
3. Policy Iteration
4. (Iterative) Policy Evaluation

QUESTION 1 OF 4

Finds the optimal policy through successive rounds of evaluation and improvement.

QUESTION 2 OF 4

Given a value function corresponding to a policy, proposes a better (or equal) policy.

QUESTION 3 OF 4

Computes the value function corresponding to an arbitrary policy.

QUESTION 4 OF 4

Finds the optimal policy through successive rounds of evaluation and improvement (where the evaluation step is stopped after a single sweep through the state space).